HP 35s scientific calculator Handleiding
HP
Rekenmachine
35s scientific calculator
Lees hieronder de 📖 handleiding in het Nederlandse voor HP 35s scientific calculator (382 pagina's) in de categorie Rekenmachine. Deze handleiding was nuttig voor 87 personen en werd door 2 gebruikers gemiddeld met 4.5 sterren beoordeeld
Pagina 1/382

HP
35s Wetenschappelijke rekenmachine
Gebruikershandleiding
H
Editie 1
HP artikelnummer F2215AA-90013

Mededeling
Het REGISTER JE PRODUCT AAN: www.register.hp.com
DE INHOUD VAN DEZE HANDLEIDING EN DE HIERIN VERVATTE
FICTIEVE PRAKTIJKVOORBEELDEN KUNNEN ZONDER AANKONDIGING
VERANDERD WORDEN. HEWLETT-PACKARD COMPANY GEEFT GEEN
GARANTIE AF VAN WELKE AARD DAN OOK MET BETREKKING TOT
DEZE HANDLEIDING, WAARONDER OOK STILZWIJGENDE GARANTIES
VAN VERHANDELBAARHEID, GESCHIKTHEID VOOR EEN BEPAALD DOEL
EN GEEN INBREUK VORMEND VAN TOEPASSING ZIJN, MAAR DIE HIER
NIET TOT BEPERKT ZIJN.
HEWLETT-PACKARD CO. KAN NIET AANSPRAKELIJK WORDEN
GESTELD VOOR ENIGERLEI FOUTEN OF VOOR INCIDENTELE OF
GEVOLGSCHADE IN VERBAND MET LEVERING, PRESTATIE OF GEBRUIK
VAN DEZE HANDLEIDING OF DE HIERIN VERVATTE VOORBEELDEN.
© 1988, 1990-1991, 2003, 2007 Hewlett-Packard Development Company, L.P.
Vermenigvuldiging, aanpassing, of vertaling van deze handleiding is, behalve
zoals toegestaan onder de auteurswet, niet toegestaan zonder eerder schriftelijke
toestemming van Hewlett-Packard Company.
Hewlett-Packard Company
16399 West Bernardo Drive
MS 8-600
San Diego, CA 92127-1899
USA
Oplage
Editie 1 Februari 2007

Inhoud 1
Inhoud
Deel 1. Principiële bediening
1. Kennismaking.............................................................1-1
Belangrijke aanwijzingen ......................................................... 1-1
De rekenmachine aan-en uitzetten ........................................ 1-1
Contrast van het scherm bijstellen ......................................... 1-1
Functies van het toetsenbord en het scherm................................. 1-2
De shift-toetsen ................................................................... 1-2
Lettertoetsen ....................................................................... 1-3
Cursortoetsen ..................................................................... 1-3
Backspace en wissen .......................................................... 1-4
Menu’s gebruiken............................................................... 1-6
Menu’s afsluiten ................................................................. 1-8
De standen RPN en ALG...................................................... 1-9
Undo toets ....................................................................... 1-11
Het scherm en de annunciators ......................... 1-12
Getallen invoeren .................................................................. 1-15
Negatieve getallen ........................................................... 1-15
Machten van tien.............................................................. 1-15
De Invoer cursor begrijpen................................................. 1-17
Bereik van getallen en OVERFLOW .................................... 1-17
Aritmetische berekeningen uitvoeren ........................................ 1-18
Enkel argument of Unair gebruik ........................................ 1-18
Twee Argument of Binaire bewerkingen .............................. 1-19
De weergave op het scherm ................................................... 1-21
Punten en komma’s in getallen (*) (8).................................. 1-23
2Inhoud
Complex getal schermweergave (º¸, º-¸, T·‚)....................1-24
De volledige 12-bits precisie tonen......................................1-25
Breuken ................................................................................1-26
Breuken invoeren ..............................................................1-26
Berichten...............................................................................1-27
Geheugen van de rekenmachine..............................................1-28
Het beschikbare geheugen bekijken ....................................1-28
Het hele geheugen wissen..................................................1-29
2. RPN: De automatische geheugenstapel ........................2-1
Wat is de stapel?.....................................................................2-1
De registers X en Y staan op het scherm.................................2-3
Het X-register wissen............................................................2-3
De stapel bekijken...............................................................2-3
Het X- en Y-register op de stapel verwisselen ..........................2-4
Rekenen - Hoe de stapel het doet ...............................................2-5
Hoe ENTER werkt................................................................2-6
Hoe wordt de stapel leeggemaakt.........................................2-7
Het register LAST X...................................................................2-8
Fouten verbeteren met LAST X...............................................2-9
Getallen opnieuw gebruiken met LAST X ..............................2-10
Kettingberekeningen met RPN..................................................2-12
Werken vanuit de haakjes..................................................2-12
Oefeningen ......................................................................2-14
Volgorde van berekening...................................................2-14
Meer oefeningen...............................................................2-16
3. Gegevens in variabelen opslaan..................................3-1
Getallen opslaan en oproepen ..................................................3-2
Een variabele bekijken .............................................................3-4
Inhoud 3
De MEM Catalogus gebruiken .................................................. 3-4
De VAR catalogus............................................................... 3-4
Rekenen met opgeslagen variabelen.......................................... 3-6
Reken met opslag ............................................................... 3-6
Rekenen met oproepen........................................................ 3-7
Een variabele met X verwisselen................................................ 3-8
De variabele “I” en “J”............................................................. 3-9
4. Functies voor reële getallen .........................................4-1
Exponentiële en logarithmische functies...................................... 4-1
Quotiënt en rest bij deling ........................................................ 4-2
Machtfuncties.......................................................................... 4-2
Trigonometrie.......................................................................... 4-3
π invoeren ......................................................................... 4-3
De hoekmodus ................................................................... 4-4
Trigonometrische functies..................................................... 4-4
Hyperbolische functies ............................................................. 4-6
Percentagefuncties................................................................... 4-6
Natuurkundige constanten ........................................................ 4-8
Conversiefuncties................................................................... 4-10
Rechthoekige/Polaire Conversies........................................ 4-10
Tijdconversies .................................................................. 4-13
Hoekconversies ................................................................ 4-13
Eenheidsconversies ........................................................... 4-14
Waarschijnlijkheidsfuncties..................................................... 4-15
Faculteit........................................................................... 4-15
Gamma........................................................................... 4-15
Waarschijnlijkheid............................................................ 4-15
Delen van getallen................................................................. 4-17
4Inhoud
5. Breuken......................................................................5-1
Breuken invoeren .....................................................................5-1
Breuken op het scherm..............................................................5-2
Regels voor de weergave.....................................................5-2
Nauwkeurigheidsannunciators..............................................5-3
De weergave van breuken veranderen .......................................5-4
Een maximum voor de noemer opgeven ................................5-4
De weergave van een breuk kiezen.......................................5-6
Voorbeelden van getoonde breuken ......................................5-8
Breuken afronden.....................................................................5-8
Breuken in vergelijkingen ..........................................................5-9
Breuken in programma’s .........................................................5-10
6. Vergelijkingen invoeren en evalueren ..........................6-1
Hoe u vergelijkingen kunt gebruiken...........................................6-1
Samenvatting van bewerkingen in vergelijkingen.........................6-3
Vergelijkingen aan de lijst van vergelijkingen toevoegen ..............6-4
Variabelen in vergelijkingen .................................................6-4
Getallen in vergelijkingen ....................................................6-5
Functies in vergelijkingen .....................................................6-5
Haakjes in vergelijkingen .....................................................6-6
Vergelijkingen weergeven en selecteren......................................6-6
Vergelijkingen bewerken en wissen............................................6-8
Soorten vergelijkingen ..............................................................6-9
Vergelijkingen evalueren.........................................................6-10
ENTER gebruiken voor evaluatie .........................................6-11
XEQ gebruiken voor evaluatie ............................................6-12
Antwoorden op de prompt van een vergelijking....................6-13
De syntaxis van vergelijkingen.................................................6-14
Inhoud 5
Volgorde van bewerkingen................................................ 6-14
Functies in vergelijkingen................................................... 6-16
Syntaxisfouten.................................................................. 6-19
Vergelijkingen controleren ...................................................... 6-19
7. Vergelijkingen oplossen ..............................................7-1
Een vergelijking oplossen ......................................................... 7-1
Ingebouwde Vergelijking oplossen........................................ 7-6
Uitleg van SOLVE .................................................................... 7-7
Het resultaat controleren...................................................... 7-7
Een SOLVE–berekening onderbreken .................................... 7-8
Beginwaarden opgeven voor SOLVE .................................... 7-8
Meer informatie..................................................................... 7-12
8. Vergelijkingen integreren ............................................8-1
Vergelijkingen integreren (∫ FN) ................................................ 8-2
Nauwkeurigheid van integratie ................................................. 8-6
Nauwkeurigheid opgeven ................................................... 8-6
De nauwkeurigheid interpreteren.......................................... 8-6
Meer informatie....................................................................... 8-8
9. Bewerkingen met complexe getallen ............................9-1
De complexe stapel ................................................................. 9-2
Complexe bewerkingen............................................................ 9-2
Complexe getallen in polaire notatie.......................................... 9-5
Complexe getallen in Vergelijkingen.......................................... 9-7
Complex getal in een programma ............................................. 9-8
10.Vector berekening.....................................................10-1
Vectorbewerkingen................................................................ 10-1
Absolute waarde van de vector .......................................... 10-3
6Inhoud
Uitwendig product.............................................................10-4
Hoek tussen vectoren.........................................................10-5
Vectoren in Vergelijkingen ......................................................10-6
Vectoren in Programma’s ........................................................10-7
Vectors creëren uit Variabelen of Registers ................................10-8
11.Conversies en berekeningen met talstelsels ................11-1
Rekenen met talstelsels 2, 8 en 16 ...........................................11-4
De representatie van getallen ..................................................11-6
Negatieve getallen............................................................11-6
Bereik van getallen............................................................11-7
Vensters voor lange binaire getallen....................................11-8
Talstelsels gebruiken in programma en vergelijkingen............11-8
12.Statistische bewerkingen ...........................................12-1
Statistische gegevens invoeren.................................................12-1
Gegevens met één variabele invoeren .................................12-2
Gegevens met twee variabelen invoeren ..............................12-2
Fouten verbeteren in de gegevensinvoer ..............................12-2
Statistische berekeningen ........................................................12-4
Gemiddelde .....................................................................12-4
Standaardafwijking van een steekproef ...............................12-6
Standaardafwijking van bevolking ......................................12-7
Lineaire regressie ..............................................................12-7
Nauwkeurigheidsbeperkingen van de gegevens ......................12-10
Waarden in de statistische registers optellen ...........................12-11
Statistieken sommeren......................................................12-11
Toegang tot de statistische registers...................................12-12
Inhoud 7
Deel 2. Programmeren
13.Eenvoudig programmeren .........................................13-1
Een programma ontwerpen .................................................... 13-3
Een stand selecteren ......................................................... 13-3
Programmagrenzen (LBL en RTN)........................................ 13-4
Gebruik van RPN, ALG en vergelijkingen in programma’s ..... 13-4
Invoer en uitvoer van gegevens .......................................... 13-5
Een programma invoeren ....................................................... 13-6
Functies wissen en backspace toets..................................... 13-7
Functienamen in programma’s ........................................... 13-8
Een programma uitvoeren..................................................... 13-10
Een programma uitvoeren (XEQ) ...................................... 13-10
Een programma testen .................................................... 13-11
Gegevens in-en uitvoeren ..................................................... 13-12
INPUT gebruiken voor invoer ........................................... 13-13
VIEW gebruiken voor het weergeven van gegevens............ 13-15
Vergelijkingen gebruiken om berichten weer te geven......... 13-16
Gegevens weergeven zonder te stoppen ........................... 13-18
Een programma stoppen of onderbreken................................ 13-19
Een stop of pauze programmeren (STOP, PSE) ................... 13-19
Een lopend programma onderbreken................................ 13-19
Fouten in programma’s.................................................... 13-19
Een programma bewerken.................................................... 13-20
Programmageheugen........................................................... 13-21
Programmageheugen bekijken ......................................... 13-21
Geheugengebruik........................................................... 13-22
De catalogus van programma’s (MEM) ............................. 13-22
8Inhoud
Een of meer programma’s wissen......................................13-23
De controlesom...............................................................13-23
Niet-programmeerbare functies..............................................13-24
Programmeren met BASE ......................................................13-25
Een talstelsel kiezen in een programma..............................13-25
Getallen die in programmaregels zijn ingevoerd.................13-25
Veeltermexpressies en het schema van Horner.........................13-26
14.Programmeringstechnieken .......................................14-1
Routines in Programma’s.........................................................14-1
Subroutines aanroepen (XEQ, RTN).....................................14-1
Geneste subroutines ..........................................................14-2
Vertakken (GTO)....................................................................14-4
Een geprogrammeerde GTO-instructie .................................14-5
GTO gebruiken op het toetsenbord .....................................14-5
Voorwaardelijke instructies......................................................14-6
Vergelijkingen (x?y, x?0) ...................................................14-7
Flags ...............................................................................14-9
Lussen.................................................................................14-16
Voorwaardelijke lussen (GTO) ..........................................14-17
Lussen met tellers (DSE, ISG).............................................14-18
Variabelen en labels indirect adresseren.................................14-20
De variabele “I” en “J” ....................................................14-20
Het indirecte adres, (I) en (J).............................................14-21
Programmabesturing met (I)/(J) .........................................14-23
Vergelijkingen met (I)/(J) ..................................................14-23
Naamloze indirecte variabelen.........................................14-23
15.Programma’s oplossen en integreren .........................15-1
Een Programma oplossen........................................................15-1
Inhoud 9
SOLVE in een programma gebruiken ....................................... 15-6
Integreren met een programma ............................................... 15-7
Integratie in een programma................................................. 15-10
Beperkingen bij het oplossen en integreren............................. 15-11
16.Statistische programma’s...........................................16-1
Curve fitting.......................................................................... 16-1
Normale en inverse verdelingen............................................ 16-11
Gegroepeerde standaardafwijking ........................................ 16-19
17.Diverse programma’s en vergelijkingen .....................17-1
Tijdwaarde van geld.............................................................. 17-1
Generator van priemgetallen .................................................. 17-7
Inwendig product in Vectoren ............................................... 17-11
Deel 3. Aanhangsels en Referentie
A. Ondersteuning, batterijen en service ........................... A-1
Ondersteuning van de rekenmachine......................................... A-1
Antwoorden op veelgestelde vragen ..................................... A-1
Bedrijfsomgeving..................................................................... A-2
De batterijen vervangen ........................................................... A-3
De werking van de rekenmachine controleren.............................A-4
De zelftest............................................................................... A-5
Garantie ................................................................................A-7
Klantenondersteuning...............................................................A-8
Gereguleerde informatie ........................................................ A-12
Federale communicatie commissie opmerking ........................... A-12
B. Het gebruikersgeheugen en de stapel ..........................B-1
Het geheugen beheren............................................................. B-1
10 Inhoud
De rekenmachine resetten .........................................................B-2
Geheugen wissen ....................................................................B-3
De toestand van het optillen van de stapel ..................................B-4
Uitschakelende bewerkingen ................................................B-5
Neutrale bewerkingen .........................................................B-5
De toestand van het register LAST X ...........................................B-6
Stapel Register Inhoud ..............................................................B-7
C. ALG: Samenvatting .....................................................C-1
Informatie over ALG ................................................................ C-1
Rekenen met twee getallen in ALG ............................................ C-2
Eenvoudig rekenen............................................................. C-2
Machtfuncties .................................................................... C-3
Percentageberekeningen..................................................... C-3
Permutaties en combinaties.................................................. C-4
Quotiënt en rest bij deling ................................................... C-4
Berekeningen met haakjes........................................................ C-4
Exponentiële en logarithmische functies ..................................... C-5
Trigonometrische functies ......................................................... C-6
Hyperbolische functies ........................................................ C-6
Delen van getallen .................................................................. C-7
De stapel bekijken................................................................... C-7
Een vergelijking integreren....................................................... C-8
Bewerkingen met complexe getallen.......................................... C-8
Rekenen met talstelsels 2, 8 en 16 .......................................... C-10
Statistische gegevens met twee variabelen invoeren .................. C-11
D. Meer over het oplossen met SOLVE............................. D-1
Hoe SOLVE een wortel vindt......................................................D-1
Resultaten interpreteren.............................................................D-3
Inhoud 11
Als SOLVE geen wortel kan vinden ............................................ D-8
Afrondfouten......................................................................... D-13
E. Meer over integratie....................................................E-1
Hoe de integraal geëvalueerd wordt.......................................... E-1
Voorwaarden waaronder er onjuiste resultaten ontstaan............... E-2
Condities die de rekentijd verlengen .......................................... E-7
F. Berichten
G. Index van bewerkingen
H. Index

Deel 1
Principiële bediening

Kennismaking 1-1
1
Kennismaking
Belangrijke aanwijzingen
De rekenmachine aan-en uitzetten
Om de rekenmachine aan te zetten, drukt u op . Onder de toets staat ON.
Om de rekenmachine uit te schakelen, drukt u op z. Dat wil zeggen, u drukt
op de shift-toets z, laat die weer los en drukt daarna op (Boven de toets
staat in gele letters OFF). De rekenmachine heeft een Continu geheugen dus de
opgeslagen informatie blijft behouden als u de rekenmachine uitschakelt.
Om energie te sparen, schakelt de rekenmachine vanzelf uit na 10 minuten van
inaktiviteit. Als u de indicator (¤) op het scherm ziet verschijnen, dan zijn de
batterijen bijna leeg. Vervang ze zo snel mogelijk. Instructies leest u in aanhangsel
A.
Contrast van het scherm bijstellen
Het contrast is afhankelijk van de verlichting, de zichthoek en de contrastinstelling.
Om het contrast te vergroten of te verkleinen, houdt u de toets ingedrukt en
drukt u op of .
Let op dit symbool in de marge. Het duidt op voorbeelden of
toetscombinaties die alleen in de RPN-stand werken. IN de ALG-
stand zijn ze anders.
Appendix C legt uit hoe u de rekenmachine in de ALG-stand gebruikt.
v

1-2 Kennismaking
Functies van het toetsenbord en het scherm
De shift-toetsen
Iedere toets heeft drie functies: de eerste is op de toets gedrukt, de tweede functie
werkt met de linker shifttoets (geel) en de derde met de rechter shifttoets (blauw). De
namen van de twee shift-functies staan in geel boven en in blauw onder iedere
toets. Druk eerst op de gewenste shift-toets (z of {) en daarna op de
functietoets voor de gewenste functie. Bijvoorbeeld, om de rekenmachine uit te
zetten, drukt u eerst op de shift-toets z en daarna op .

Kennismaking 1-3
Drukt u op z of { dan verschijnt het symbool of ¡ bovenin het scherm.
Dit is een annunciator. De annunciator verdwijnt als u op de volgende toets drukt.
Om een shift-toets te annuleren (en de annunciator uit te schakelen), drukt u
opnieuw op dezelfde shift-toets.
Lettertoetsen
De meeste toetsen geven een letter weer in hun onderrechterhoek, zoals u hierboven
ziet. Moet u een letter typen (bijvoorbeeld een variabele of een label
van een
programma) dan verschijnt de annunciator A..Z in het scherm, wat aangeeft dat de
toetsen nu als lettertoetsen “werken“.
Variabelen worden besproken in hoofdstuk 3; labels worden besproken in
hoofdstuk 13.
Cursortoetsen
Elke van de vier cursor richtingstoetsen is gemarkeerd met een pijltje. In deze tekst
gebruiken we Õ, Ö, × en Ø als we het over deze toetsen hebben.
Functie met
linkershift
Functie met
rechtershift
Letter voor
alfabetische toets

1-4 Kennismaking
Backspace en wissen
Een van de eerste dingen die u moet weten is hoe u een invoer moet wissen, een
getal moet corrigeren en het gehele scherm moet wissen om opnieuw te beginnen.
Wistoetsen
Toets Omschrijving
aBackspace.
Als een expressie wordt ingevoerd, verwijdert a het teken naar
de linkerkant van de invoer cursor (_). Anders, met een afgeronde
expressie of door een resultaat in regel 2, vervangt a dat
resultaat met nul. a wist ook fout- meldingen en verlaat menu’s.
a gedraagt zich gelijkwaardig wanneer de rekenmachine in
programma en vergelijkingen standen staat, zoals hieronder
besproken:
Invoer van vergelijkingen:
Als een vergelijking wordt ingevoerd of bewerkt, verwijdert
a het teken onmiddelijk naar de linkerkant van de invoer
cursor; anders, als de vergelijking is ingevoerd (zonder een
invoeg cursor), verwijdert a de gehele vergelijking.
Programma-invoer:
Wanneer een programma regel wordt ingevoerd of bewerkt,
verwijdert a het teken naar de linkerkant van de invoeg
cursor, anders zou a de gehele regel verwijderen als de
programmaregel wordt ingevoerd.
Wissen of Annuleren.
Wijzigt het weergegeven getal in nul of annuleert de huidige
situatie (zoals een menu, een bericht, een prompt, een catalogus,
de invoer van een vergelijking of van een programma).

Kennismaking 1-5
Wistoetsen (vervolg)
Toets Omschrijving
{Het WIS menu ( º # ´ ! #º )
bevat opties voor het wissen van x (het nummer in het X register),
alle direkte variabelen, het gehele geheugen, alle statische data,
alle opslag en indirekte variabelen.
Als u () drukt, verschijnt een nieuw @ &
menu zodat u uw beslissing kan bevestigen voordat alles in het
geheugen verwijdert wordt.
Wanneer een programma wordt ingevoerd, wordt
vervangen door . Als u op () drukt, wordt een
nieuw @ & menu weergegeven, zodat u uw besluit
kan bevestigen voordat alle programma’s worden gewist.
Wanneer een vergelijking wordt ingevoerd, wordt
vervangen door . Als u () drukt, wordt het
@ & menu weergegeven, zodat u uw besluit kan bevestigen
voordat alle vergelijkingen worden verwijderd.
Wanneer u (#º) selecteert, wordt het commando
geplakt in de commando regel met drie plaatshouders. U moet
een 3-cijferig getal in de lege velden van de plaatshouder
invoeren. Alle indirekte variabelen wiens adressen groter zijn dan
de ingevoerde, worden dan gewist. Bijvoorbeeld: CLVAR056 wist
alle indirekte variabelen wiens adres groter is dan 56.

1-6 Kennismaking
Menu’s gebruiken
De HP 35s kan heel wat meer dan u op het toetsenbord ziet. Dat komt doordat 16
van de toetsen menutoetsen zijn. Er zijn in totaal 16 menu’s, die veel meer functies
bieden, of meer opties voor meer functies.
HP 35s Menu’s
Menunaam Menubeschrijving Hoofdstuk
Numerieke functies
L.R. T P E
Lineaire regressie: fitten van een curve en
lineaireschatting.
12
,
Aritmetisch gemiddelde van statistische x– en y–
waarden; gewogen gemiddelde van statistische x–
waarden.
12
s,σUº U¸ σº σ¸
Standaardafwijking van een steekproef,
Standaardafwijking van de bevolking.
12
CONST Menu voor de 41 fysieke constanten-zie “Fysieke
constanten” op pagina 4–8.
4
SUMS Q ;º ;¸ ;º ;¸ ;º¸
Statistische sommering van gegevens.
12
BASE % ! G K µ E
Conversie naar andere talstelsels (decimaal,
hexadecimaal, octaal en binair).
12
INTG !÷ PGT !
Teken, gehele deling, restant van deling, grootste
gehele getal, het gebroken deel, het gehele deel.
4,C
LOGIC % !
Logische operators
11
º
ˆ¸
ˆ
xyº ¸ ·º

Kennismaking 1-7
Een menufunctie gebruiken:
1. Druk een menu toets om een set menu objecten weer te geven.
2. Druk op Õ Ö × Ø om de onderstreping op het gewenste object te
zetten.
3. Druk op als het gewenste object onderstreept is.
Zijn de objecten genummerd, dan kunt u op drukken terwijl het object
onderstreept is, maar u kunt ook direct het nummer invoeren.
Programmeringinstructies
FLAGS @
Functies om vlaggen te zetten, te wissen en te testen.
14
x?y≠ ≤ < > ≥ =
Vergelijking tussen het X– en Y–register.
14
x?0≠ ≤ < > ≥ =
Vergelijking tussen het X–register en nul.
14
Weitere Funktionen
MEM #
Toestand van het geheugen (beschikbare bytes in het
geheugen); catalogus van variabelen; catalogus van
programma’s (programmalabels).
1, 3, 12
MODE
Graden en gebruik
4, 1
DISPLAY % * 8 8 º¸
º-¸ T
Vast, wetenschappelijk, engineering, vol drijvende
komma in getallen weergegeven formaten; grondtal
symbool opties (.of ,); complex getal weergave
formaat (in RPN, alleen xiy en rθa)
1
R¶ R µ% & ' !
Functies om de stapel in de ALG-stand te bekijken -
Register X, Y, Z, T
C
CLEAR Functies om delen van het geheugen te wissen—zie
{ in de tabel op pagina 1–5.
1, 3,
6, 12

1-8 Kennismaking
Sommige menu’s, zoals CONST en SUMS, hebben meer dan een pagina. Het
invoeren van deze menu’s zal de © of ª annunciator aanzetten. In deze menu’s,
gebruik de Õ en Ö cursor toetsen om naar een item op de huidige menu
pagina te nagiveren, gebruik de Ø en × toetsen voor de volgende en vorige
pagina’s in het menu.
Voorbeeld:
In dit voorbeeld gebruiken we het DISPLAY menu om de weergave van 4 decimale
getallen vast te zetten en 6÷7 te berekenen. Het voorbeeld sluit af met het DISPLAY
menu en keert terug naar de drijvende komma weergave van getallen.
Menus helpen u met het uitvoeren van een heleboel functies door u te begeleiden.
U hoeft niet de namen van alle ingebouwde functies te onthouden van de
rekenmachine, en ook niet te zoeken naar de functies op het toetsenbord.
Menu’s afsluiten
Wanneer u een menufunctie uitvoert, verdwijnt het menu automatisch, zoals in het
voorbeeld hierboven. Wilt u een menu verlaten zonder
een functie uit te voeren,
dan hebt u de volgende drie opties:
Invoer: Weergave: Omschrijving:
Eerste weergave
z8%
DISPLAY menu invoeren
of % Het Fix commando is geplakt in
regel 2
)
)
4 decimale plaatsen vastzetten
p )
)
De deling uitvoeren
z8
).
Terugkeren naar volledige precisie

Kennismaking 1-9
Door op a te drukken, verlaat het 2- niveau menu CLEAR of MEM, met een
niveau tegelijk. Zie { in de tabel op pagina 1–5.
Door op a of te drukken verlaat u ieder ander menu.
Door op een andere menutoets te drukken vervangt u het oude menu door
een nieuw.
De standen RPN en ALG
De rekenmachine kan berekeningen uitvoeren in RPN (omgekeerde Poolse notatie)
of ALG (algebraïsche notatie).
In omgekeerde Poolse notatie (RPN) wordt het tussenresultaat van de berekeningen
automatisch opgeslagen. U gebruikt dus geen haakjes.
In algebraïsche notatie, (ALG), kunt u aritmetische berekeningen uitvoeren met de
standaard volgorde van berekeningen.
RPN kiezen:
Druk op 9{() om de rekenmachine in de stand RPN te zetten.
Wanneer de rekenmachine in de RPN stand staat, is de RPN annunciator
aangezet.
Invoer: Weergave:
)_
z8% ª
@ of )_
Invoer: Weergave:
)_
z8% ª
{% # ª
)
;

1-10 Kennismaking
ALG kiezen:
Druk op 9{() om de rekenmachine in de stand ALG te zetten.
Wanneer de rekenmachine in de ALG stand staat, is de ALG annunciator
aangezet.
Voorbeeld:
Stel dat u wilt berekenen 1 + 2 = 3.
In de RPN-stand voert u het eerste getal in, drukt u op , voert u het tweede
getal in en drukt u tenslotte op de toets om de berekening uit te voeren.
In de stand ALG geeft u eerst het eerste getal op, vervolgens drukt u op ,
daarna geeft u het tweede getal op en tenslotte drukt u op de toets .
In de ALG-stand worden de resultaten en berekeningen getoond. In de RPN-stand
ziet u alleen de resultaten, niet de berekeningen.
RPN stand ALG stand
1 2 1 2
Opmerking U kunt voor uw berekeningen kiezen tussen ALG (algebraïsch) of
RPN (omgekeerd Pools). In deze handleiding gebruiken we het
teken “v” in de marge om aan te geven dat de toetsaanslagen in
ALG en RPN niet dezelfde zijn. In Aanhangsel C wordt uitgelegd
hoe u de rekenmachine in de ALG-stand gebruikt.
Kennismaking 1-11
Undo toets
De Undo toets
Het gebruik van de Undo(ongedaan maken) toets, hangt af van de context van de
rekenmachine, maar dient voornamelijk voor het herstellen van een verwijderde
invoer en niet voor het ongedaan maken van elke willekeurige berekening. Zie Het
laatste X Register in Hoofdstuk 2 voor details over het terugroepen van een invoer in
regel 2 van het scherm nadat een nummerieke functie is uitgevoerd. Druk
onmiddelijk z: na het gebruik van a of om:
een invoer te herstellen die u heeft verwijderd
een vergelijking verwijderd wanneer er met vergelijkingen wordt gewerkt
Een programmalijn verwijderd wanneer er met programma’s wordt gewerkt
Als toevoeging, kunt u Undo gebruiken om de waarde van een register te herstellen
die net is gewist na het gebruik van het CLEAR menu. Undo moet onmiddelijk
gebruikt worden na de verwijdering; elke onderbreking zal Undo het terughalen
van het verwijderde objekt doen tegenhouden. Voor het terughalen van een gehele
invoer na haar verwijdering, kan Undo ook gebruikt worden tijdens het bewerken
van een invoer. Druk z: tijdens bewerking voor het terughalen van:
een cijfer in een expressie dat u net heeft verwijderd met a
een expressie dat u aan het bewerken was maar is gewist door
een teken in een vergelijking of programma dat u net met a heeft
verwijderd (terwijl het in de vergelijking of programma stand stond)
let op dat het gebruik van Undo is beperkt door de hoeveelheid beschikbare
geheugen.
1-12 Kennismaking
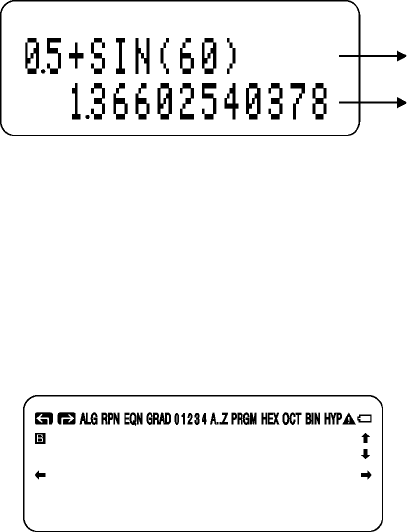
Het scherm en de annunciators
Het scherm bestaat uit twee regels tekst en de annunciators.
Invoeren met meer dan 14 tekens scrollen naar links. Tijdens het invoeren, wordt de
invoer in de eerste regel van ALG weergegeven en de tweede regel in RPN. Elke
berekening is weergegeven tot 14 cijfers, inclusief een teken (macht) en
machtswaarde tot drie cijfers.
De tekens op het scherm, die hierboven zijn getoond, heten annunciators. Elke
annunciator heeft een bepaalde betekenis.
Eerste regel
Tweede regel
Annunciators

Kennismaking 1-13
HP 35s Annunciators
Annunciator Betekenis Hoofdstuk
¢De “¢ (Bezig)” annunciator verschijnt als
er een bewerking, vergelijking of
programma wordt uitgevoerd.
c
d
In de stand voor breukweergave (druk op
{ ), wordt slechts een van de
twee helften “c” of “d” van de
annunciator “cd” getoond om aan te
geven of de getoonde noemer iets minder
of iets meer is dan de werkelijke waarde.
Ziet u “cd” helemaal niet, dan wordt de
nauwkeurige waarde van de breuk
weergegeven.
5
Linker shift is actief. 1
¡Rechter shift is actief. 1
RPN Er wordt gewerkt in omgekeerde Poolse
notatie.
1, 2
ALG Er wordt gewerkt in algebraïsche notatie. 1, C
PRGM Programma-invoer is actief. 13
EQN Er wordt een vergelijking ingevoerd, of de
rekenmachine is bezig met het evalueren
van een expressie of het uitvoeren van een
vergelijking.
6
0 1 2 3 4 Geeft aan welke flags zijn gezet (de flags 5
tot en met 11 hebben geen annunciator).
14
RAD of GRAD Er wordt gewerkt met radialen of decimale
graden. De standaardstand DEG heeft geen
annunciator.
4
HEX OCT BIN Geeft het huidige talstelsel aan. De
standaardstand DEC (decimaal) heeft geen
annunciator.
11
HYP Hyperbolische functie is aktief. 4, C

1-14 Kennismaking
HP 35s Annunciators (vervolg)
Annunciator Betekenis Hoofdstuk
§,¨Er zijn meer tekens aan de linker of
rechterkant in het scherm van de invoer in
regel 1 of regel 2. Beide annunciators kunnen
tegelijk verschijnen, aangevend dat er tekens
zijn aan de linker en rechterkan in het scherm
van de invoer. Invoeren in regel 1 met gemiste
tekens worden getoond met een
weglatingsteken (...) om aan te geven dat er
tekens ontbreken. In RPN, gebruik de Õ en
Ö toetsen om door een invoer te scrollen en
de om de voor en achter tekens te zien. In
ALG, gebruik {Õ en {Ö om ook
de andere tekens te zien.
1, 6
©,ªDe Ø en × toetsen zijn actief voor het
doornemen van een vergelijkingslijst, een
cataloog van variabelen, regels van een
programma, menu pagina’s, of programma’s
in de programma catalogus.
1, 6, 13
A..Z De lettertoetsen zijn actief. 3
£Let op! Dit geeft een speciale conditie of fout
aan.
1
¤Batterij is bijna leeg. A

Kennismaking 1-15
Getallen invoeren
De minimum en maximum waarden die een rekenmachine kan hanteren zijn
±9,99999999999499. Als het resultaat van een berekening meer is dan dit,
verschijnt de foutmelding “#$” even samen met de £ annunciator. Het
overloop bericht wordt dan vervangen door de waarde die de overloop limiet het
dichtst benaderd en dat de rekenmachine kan weergeven. De kleinste getallen die
de rekenmachine kan onderscheiden zijn die van nul tot ±10-499. Als u een getal
invoert ergens tussen deze waarden, geeft de rekenmachine 0 weer na invoer. Ook
als het resultaat van de berekening ergens tussen deze twee waarden ligt, zal het
resultaat worden weergegeven als nul. Nummers invoeren die hoger zijn dan het
maximum bereik, zal een foutmelding “# !” als resultaat hebben: het
wissen van de foutmelding brengt u terug naar de vorige invoer voor het corrigeren
van uw fout.
Negatieve getallen
Met de toets _ verandert u het teken van een getal.
Om een negatief getal in te voeren, voert u het getal in en drukt u vervolgens
op _,
In ALG, kunt u op de _ toets drukken voor of na het typen van het getal.
Om het teken te veranderen van een getal dat al eerder is ingevoerd, drukt u
op _. (Heeft het getal een exponent, dan verandert _ alleen de
mantisse
— het deel van het getal dat niet de exponent is.)
Machten van tien
Exponenten op het scherm
Getallen met expliciete machten van tien (zoals 4,2x10-5 ) worden weergegeven
met een E voor de macht van 10. Dus 4,2x10-5 wordt ingevoerd en weergegeven
als 4,2E-5.
Is de absolute waarde van een getal te groot of te klein voor het scherm, dan wordt
het automatisch in exponentiële vorm weergegeven.
Bijvoorbeeld, u hebt FIX 4 gekozen voor vier cijfers achter de komma. Let nu op het
effect van de volgende toetsaanslagen:
1-16 Kennismaking
Machten van tien invoeren
De ` toets wordt gebruikt om machten van tien snel in te voeren. Bijvoorbeeld, in
plaats van een miljoen als 1000000 kunt u eenvoudig ` invoeren. Het
volgende voorbeeld verduidelijkt het proces en ook hoe de rekenmachine het
resultaat weergeeft.
Voorbeeld:
Stel dat u Planck’s constant wilt invoeren: 6,6261×10-34
Voor een macht van tien zonder vermenigvuldiger, zoals in het voorbeeld van een
miljoen hierboven, druk op de ` toets gevolgd door het gewenste exponent
van tien.
Invoer: Weergave: Omschrijving:
)_Toont het ingevoerde getal.
) Rondt het getal af op vier cijfers achter
de komma.
). Gebruikt automatisch
wetenschappelijke notatie omdat er
anders geen significante cijfers zouden
verschijnen.
Invoer: Weergave: Omschrijving
)_
Mantisse invoeren
`
)_Equivalent ×10x invoeren
z).
).
Exponent invoeren
Kennismaking 1-17
Andere exponentfuncties
Om een macht van tien te berekenen (de anti-logaritme met grondtal 10), gebruik
z (. Om het resultaat te berekenen van een willekeurig getal in een macht
(machtsverheffen), drukt u op 0 (zie hoofdstuk 4).
De Invoer cursor begrijpen
Terwijl u een getal invoert, verschijnt de cursor (_) en blinkert op het scherm. De
cursor geeft aan waar het volgende cijfer komt en geeft dus ook aan dat het getal
nog niet voltooid is.
Als u een functie uitvoert voor het berekenen van een resultaat, verdwijnt de cursor
omdat het getal voltooid is-de invoer is beëindigd.
Drukt u op dan wordt de invoer voltooid. Om twee getallen te scheiden,
toetst u eerst het eerste getal in. Daarna drukt u op om de invoer te
beëindigen, en daarna toetst u het tweede getal in.
Als de invoer niet beëindigd is (als de cursor niet aanwezig is), gaat a terug om
het laatste cijfer te wissen. Als de invoer is beëindigd (geen cursor), handelt a
als en verwijdert het gehele getal. Probeer het uit!
Bereik van getallen en OVERFLOW
Het kleinste getal in de rekenmachine is –9,99999999999 × 10499, terwijl het
grootste getal 9,99999999999 × 10499 is.
Resulteert een berekening in een getal dat groter is dan het maximum, dan is
het resultaat –9,99999999999 × 10499 of 9,99999999999 × 10499 en de
waarschuwing #$ verschijnt.
Invoer: Weergave: Omschrijving:
_Invoer niet beëindigd: het getal is niet
voltooid.
<) Invoer is beëindigd.
) Een voltooid getal.
) Nog een voltooid getal.

1-18 Kennismaking
Aritmetische berekeningen uitvoeren
De HP 35s kan zowel in de RPN stand als ook in de algebraïsche stand (ALG)
gebruikt worden. Deze standen beïnvloeden hoe expressies worden ingvoerd. De
volgende secties geven de invoerverschillen aan voor een enkel argument (of
unaire) en twee argumenten (of binaire).
Enkel argument of Unair gebruik
Sommige van de numerieke bedieningen van de HP 35s vereisen een enkel getal
als invoer, zoals 3, :, &en k. Deze enkele argumenten worden
verschillend ingevoerd, dit hangt van of de rekenmachine in de RPN of ALG stand
staat. In de RPN stand, wordt het getal eerst ingevoerd en dan toegepast. Als de
toets is ingedrukt nadat het getal is ingevoerd, verschijnt het getal in regel
1 en het resultaat wordt weergegeven in regel 2. Anders, wordt het resultaat
gewoon weergegeven in regel 2 en regel 1 blijft onveranderd. In de ALG stand,
wordt de operator eerst ingedrukt en het scherm geeft de functie weer, gevolgd
door een paar haakjes. Het nummer wordt ingevoerd tussen haakjes en dan wordt
de toets ingedrukt. De expressie wordt weergegeven in regel 1 en het
resultaat in regel 2. De volgende voorbeelden maken de verschillen duidelijk.

Kennismaking 1-19
Voorbeeld:
Bereken 3,42, eerst in RPN en dan in ALG.
In het voorbeeld, wordt de kwadraat operator getoond op de toets als : maar
weergegeven als SQ(). Er zijn verschillende enkele argument operators die anders
in ALG stand worden weergegeven dan ze op het op het toetsenbord verschijnen
(en ook anders verschijnen in de RPN stand). Deze zijn hieronder in de tabellijst te
zien.
Twee Argument of Binaire bewerkingen
Twee argument bewerkingen, zoals , p, ), en x, zijn ook anders
ingevoerd, dit hangt af van de stand, al zijn de verschillen niet groot met de enkele
argument bewerkers. In de RPN stand, wordt het eerste getal ingevoerd, het tweede
getal wordt dan geplaatst in het x-register en de twee argument bewerking is
opgeroepen. In de ALG stand, zijn er twee gevallen, een met gebruik van
traditionele infix-notatie en een andere die een wat meer functie georiënteerde
aanpak toepast. De volgende voorbeelden tonen de verschillen.
Invoer: Weergave: Omschrijving:
9()RPN stand invoeren (als het nodig is)
) Getal invoeren
{:
) Druk de kwadraat operator
9()Schakelen naar de ALG stand
{: 12 Kwadraat invoeren
1)2 Voer het getal tussen haakje in
1)2
)
Druk de Enter toets voor het resultaat
Toets In RPN, RPN
Programma
In ALG, vergelijking, ALG Programma
:X2SQ()
?≡xSQRT()
#exEXP()
!10xALOG()
31/x INV()

1-20 Kennismaking
Voorbeeld
Bereken 2+3 en 6C4, eerst in RPN en dan in ALG.
In ALG, zijn de infix-operators , ,y, p, en 0. De andere twee
argumenten gebruiken functie notatie van de vorm f(x,y), waar x en y de eerste en
tweede operanden zijn in volgorde. In RPN, worden de operanden voor twee
argument bewerkingen ingevoerd in de volgorde Y, dan X op de stapel. Dat
betekent dat, y de waarde is in het y-register en x de waarde is in het x-register.
De xde bron van y(') is de uitzondering op deze regel. Bijvoorbeeld, om te
berekenen in RPN stand, druk z'. In ALG, wordt de
vergelijking ingevoerd als z ' Õ .
Net zoals met enkele argument bewerkingen, worden sommige van de twee
argument bewerkingen anders weergegeven in RPN stand dan in ALG. Deze
verschillen zijn samengevat in onderstaande tabel.
Invoer: Weergave: Omschrijving:
9()Schakelen naar de RPN stand (als het
nodig is)
_
Voer 2 in, plaats dan 3 in de x-register.
Let op de knipperende cursor na de 3;
druk niet op Enter!
Druk de opteltoets om het resultaat te
zien.
_
Voer 6 in, plaats dan 4 in de x-register.
zx
Druk de combinatietoetsen om het
resultaat te zien.
9()Schakelen naar de ALG stand
-
Expressie en resultaat worden allebei
getoond.
zxQT182 Voer de combinatie functie in.
ÕQT182 Voer de 6 in, verplaats dan de
bewerkingscursor voorbij de komma en
voer de 4 in.
QT182
Druk Enter om het resultaat te zien.
38

Kennismaking 1-21
Voor vervangende bewerkingen zoals en y, beïnvloedt de volgorde van de
operands niet het berekende resultaat. Als u per ongeluk een operand heeft
ingevoerd voor een niet vervangende twee argument bewerking in de verkeerde
volgorde in RPN, druk dan de Ztoets om de inhouden van de x- en y- registers te
verwisselen. Dit is uitgelegd in detail in Hoofdstuk 2 (zie het gedeelte De X- en Y-
Registers in de stapel verwisselen).
De weergave op het scherm
Alle getallen zijn opgeslagen met een 12-cijferige precisie; maar, u kunt het aantal
cijfers gebruikt in de weergave van de cijfers controleren met de opties in het
weergave menu. Druk z8 voor toegang tot dit menu. De eerste vier
opties (FIX, SCI, ENG en ALL) controleren de aantallen cijfers in de
getallenweergave. Tijdens sommige gecompliceerde interne berekeningen, gebruikt
de rekenmachine 15- cijferige precisie voor gemiddelde resultaten. Het
weergegeven getal is afgerond volgens de weergave.
Weergave vaste decimale (%)
Met FIX wordt een getal weergegeven met maximaal 11 decimalen( 11 cijfers
rechts van de “)” of “8” komma) voor zover er ruimte is. Na de prompt %_ geeft
u het gewenste aantal decimalen op. Wenst u 10 of 11 decimalen, druk dan op
of .
Bijvoorbeeld, in het getal 8), zijn de “7”, “0”, “8” en “9” de
decimale cijfers die u ziet als de rekenmachine is ingesteld op FIX 4.
Elk getal dat te groot is (1011) of te klein (10-11) om weer te geven in de huidige
decimale plaats instelling, wordt automatisch weergegeven in wetenschappelijk
weergave.
Toets In RPN, RPN
Programma
In ALG, vergelijking, ALG
Programma
0yx^
.x√yXROOT(, )
EINT÷IDIV(, )
1-22 Kennismaking
Wetenschappelijke weergave ( )
Met SCI wordt een getal getoond in wetenschappelijke weergave: een cijfer voor
de komma “)”of “8”, maximaal 11 cijfers erachter en maximaal drie cijfers in de
exponent. Na de prompt, _, geeft u het gewenste aantal decimalen op. Wenst
u 10 of 11 decimalen, druk dan op of . (De mantisse van het getal
is altijd minder dan 10.)
Bijvoorbeeld, in het getal ), zijn de “2”, “3”, “4” en “6” de decimale
cijfers die u ziet als de rekenmachine is ingesteld op SCI 4. De “5” na de “E” is de
exponent van 10: 1,2346 × 105.
Als u een getal invoert of berekent dat meer dan 12 cijfers heeft, kan de
aangevulde precisie niet worden gehandhaafd.
Engineering weergave ()
Met ENG wordt een getal weergegeven op een manier die lijkt op
wetenschappelijke notatie, met als uitzondering dat de exponent een veelvoud van
3 is. (Er kunnen dan maximaal drie cijfers vóór de komma “)” of “8” in de mantisse
staan.) Deze weergave is handig bij wetenschappelijk werk als u voorvoegsels
gebruikt die veelvouden zijn van 103 (zoals micro–, milli– en kilo–.)
Na de prompt, _, toetst u het gewenste aantal cijfers in na het eerste
significante cijfer. Wenst u 10 of 11 cijfers, druk dan op of .
Bijvoorbeeld, in het getal ), zijn “2”, “3”, “4”, en “6” de significante
cijfers na het eerste significante cijfer dat u ziet als de rekenmachine in ENG 4
staat. De “3” na de “” is de exponent van 10, en altijd een veelvoud van 3:
123,46 x 103.
Drukt u op z@ of z2 dan verandert de getoonde exponent in
een ander veelvoud van 3, met de mantisse op de juiste manier aangepast.
Kennismaking 1-23
Voorbeeld:
Dit voorbeeld geeft het gedrag van de Engineering weergave aan met gebruik van
het getal 12,346E4. Het toont ook het gebruik van de z@ en
z2 functies. Dit voorbeeld gebruikt de RPN stand.
ALL-weergave ()
De ALL- weergave is de standaard weergave, geeft getallen weer met maximaal 12
cijferige precisie. Wanneer alle cijfers niet in het scherm passen, wordt het getal
automatisch weergegeven in wetenschappelijke weergave.
Punten en komma’s in getallen (*) (8)
De HP 35s gebruiken zowel punten en komma’s om het lezen van getallen
makkelijker te maken. U kunt ofwel de punt of de komma of het decimale punt
(radix) selecteren. Als toevoeging, kunt u kiezen of u wel of niet cijfers in groepen
van drie wilt splitsen met gebruik van duizend splitsers. Het volgende voorbeeld
toont de opties.
Invoer: Weergave: Omschrijving:
z8(
)
_Kies Engineering weergave
)
)
Voer 4 in (voor 4 significante cijfers
achter de eerste).
}
)
)
Voer in 12,346E4.
z@ of f
z2
)
)
z@)
)
Verhoog de exponent met 3
z2)
)
Verminder de exponent met 3

1-24 Kennismaking
Voorbeeld
Voer het getal 12.345.678,90 in en verander het decimale punt naar de komma.
Kies dan niet voor de duizend splitser. Tot slot, keer terug naar de standaard
instellingen. Dit voorbeeld gebruik de RPN stand.
Complex getal schermweergave (º¸, º-¸ , T)
Complexe getallen kunnen op verschillende manieren weergegeven worden: º¸,
º-¸ en T, hoewel º-¸ alleen beschikbaar is in de ALG stand. In
onderstaand voorbeeld, wordt het complexe getal 3+4i op drie manieren
weergegeven.
Invoer: Weergave: Omschrijving:
z8(
)
Selecteer drijvende komma punt
precisie (ALL weergave).
88)
88)
De standaard weergave gebruikt de
komma als de duizend splitser en de
punt als de radix.
z8(8)))8
))8
Verander om de komma te
gebruiken voor de radix. Let op dat
de duizend splitser automatisch
verandert naar de punt.
z8(
)
8
8
Verander in geen komma splitser
gebruiken.
z8(*)
z8(8
)
88)
88)
Terugkeren naar
standaardweergave.

Kennismaking 1-25
Voorbeeld
Toon het complexe getal 3+4i in elke van de verschillende weergaven.
De volledige 12-bits precisie tonen
Verandert u het aantal weergegeven decimalen, dan heeft dat invloed op wat u
ziet, maar het heeft geen invloed op de interne representatie van de getallen. Intern
wordt ieder getal met 12 cijfers opgeslagen.
Bijvoorbeeld, in het getal 14,8745632019 ziet u alleen “14,8746” als u de
rekenmachine hebt ingesteld op FIX 4. De laatste zes cijfers (“632019”) bevinden
zich alleen intern in de rekenmachine.
Om een getal tijdelijk met volledige precisie weer te geven, drukt u op z
Î. U ziet nu de mantisse
(maar niet de exponent) zolang u Î
ingedrukt houdt.
Invoer: Weergave: Omschrijving:
9()ALG stand gebruiken
6
Voer het complexe getal in. Het
wordt weergegeven als 3i4,
standaardweergave.
z8
(º-¸ )
-
Verander in x+yi weergave.
z8
(T) of
z8×
×Õ
θ)
Verander in r
θ
a weergave. De
radius is 5 en de hoek is ongeveer
53,13°.
Invoer: Weergave: Omschrijving:
y
) Vier decimalen weergegeven.
z8( )
)Wetenschappelijke weergave:
twee decimalen en een exponent.

1-26 Kennismaking
Breuken
Met de HP 35s kunt breuken invoeren en ze bewerken, ze weergeven als ofwel
decimalen of als breuken. De HP 35s geeft breuken in de vorm a b/c weer, waar a
een integer is en b en c telgetallen zijn. Als toevoeging, is b 0≤b<c en c is
1<c≤4095.
Breuken invoeren
Breuken kunnen op ieder moment op de stapel worden gezet:
1. Geef het gehele deel van het getal op en druk op . (De eerste scheidt
het gehele deel van het getal van het gebroken deel.)
2. Voer de teller van de breuk in en druk weer op . De tweede scheidt de
teller van de noemer.
3. Voer de noemer in, en druk op of een functietoets om de invoer te
beëindigen. Het resultaat wordt weergegeven volgens de geldende instelling.
Het symbool a b/c
onder de toets herinnert u eraan dat de toets twee keer
gebruikt wordt om een breuk in te voeren.
Het volgende voorbeeld toont de invoer en weergave van breuken.
z8()
)Engineering weergave.
z8()) Alle significante cijfers; nullen aan
de rechterkant worden
weggelaten.
z8(%)
) Vier decimalen, geen exponent.
3) Omgekeerde van 58,5.
z Î
(vasthouden)
Toont de volledige precisie tot u
loslaat.

Kennismaking 1-27
Voorbeeld
Voer de gemengde getallen 12 3/8 in en geef het weer in breuken en decimale
vormen. Voer dan ¾ in en tel het op bij 12 3/8. Dit voorbeeld gebruikt RPN.
Zie verder hoofdstuk 5, “Breuken,” voor meer informatie over het gebruik van
breuken.
Berichten
De rekenmachine reageert op foute condities door de £ annunciator weer te
geven. Normaal gesproken, zal een bericht te zien zijn met foute annunciator.
Om een bericht te wissen, druk of a; in de RPN stand, u keert terug
naar de stapel zoals het was voor de fout. In de ALG stand, keert u terug
naar de laatste expressie met de bewerkingscursor naar de plaats van de fout
zodat u het kunt corrigeren.
Invoer: Weergave: Omschrijving:
)
De decimale punt wordt op de normale
manier geïnterpreteerd.
)
+_
Wanneer voor de tweede keer is
ingedrukt, verandert het scherm in de
breukweergave.
)
)
Na de invoer, wordt het getal getoond
in de huidige schermweergave.
{É +
+
Verander in breukweergave.
+
+_Voer ¾ in. Let op dat u begint met
omdat er geen integer deel is (u kunt
0 ¾ intypen).
+
Tel ¾ op bij 12 3/8.
{É
)
Gaat terug naar de huidige weergave
stand.

1-28 Kennismaking
Elke andere toets zal het bericht ook wissen, hoewel de toetsfunctie niet is
ingevoerd.
Wanneer er geen bericht is weergegeven, maar de £ annunciator toch verschijnt,
heeft u een inactieve of ongeldige toets ingedrukt. Bijvoorbeeld, het indrukken van
zal £ weergeven omdat het tweede decimale punt geen betekenis heeft
in deze context.
Alle weergegeven berichten staan in aanhangsel F, “Berichten”.
Geheugen van de rekenmachine
De HP 35s heeft 30KB geheugen waarin u een willekeurige combinatie van
gegevens kunt opslaan (variabelen, vergelijkingen of programmaregels).
Het beschikbare geheugen bekijken
Met z X verschijnt het volgende menu:
#
QQQ PP8PPP
waarin
QQQ is de hoeveelheid van gebruikte indirecte variabelen.
PP8PPP het aantal bytes is van beschikbare geheugen.
Drukken op (#) geeft de catalogus van directe variabelen weer. (zie
“Bekijken van Variabelen in de VAR catalogus” in hoofdstuk 3). Het indrukken van
de () geeft de catalogus met programma’s weer.
1. Om naar de catalogus van variabelen te gaan, drukt u op (#). Om
naar de catalogus van programma’s te gaan drukt u op ().
2. Om door de catalogi te bladeren, drukt u op Ø of ×.
3. Om een variabele of een programma te verwijderen, drukt u op {
terwijl de variabele of het programma in de catalogus zichtbaar is.
4. Om de catalogus af te sluiten, drukt u op .
Kennismaking 1-29
Het hele geheugen wissen
Wist u het hele geheugen, dan worden alle getallen, vergelijkingen en
programma’s verwijderd. Het heeft geen invloed op de instellingen van modus en
weergave. (Om instellingen en gegevens te wissen, zie “Geheugen wissen” in
aanhangsel B.)
Het gehele geheugen wissen:
1. Druk op (). U ziet de bevestigingsprompt @ & , die u
beschermt tegen onbedoeld wissen van het geheugen.
2. Druk op Ö (&) .

RPN: De automatische geheugenstapel 2-1
2
RPN: De automatische geheugenstapel
Dit hoofdstuk legt u uit hoe berekeningen worden uitgevoerd in de automatische
geheugenstapel van RPN. U hoeft dit niet te lezen om de rekenmachine te kunnen
gebruiken, maar een goed begrip van dit hoofdstuk helpt u wel bij het gebruik,
vooral als u programma’s schrijft.
In deel 2, “Programmering”, leert u hoe de stapel u kan helpen om uw programma’s
te manipuleren en organiseren.
Wat is de stapel?
Automatisch opslaan van tussenresultaten
is de reden waarom de HP 35s
gemakkelijk ingewikkelde berekeningen uitvoert, zonder haakjes te gebruiken. De
sleutel van de automatische opslag is de automatische RPN-stapel.
De logica van HP is gebaseerd op een ondubbelzinnige schrijfwijze zonder
haakjes die bekend staat als de “Poolse notatie” en ontwikkeld is door de Poolse
wiskundige Jan Łukasiewicz (1878-1956).
De gebruikelijke algebraïsche notatie plaatst de operators tussen de getallen of
variabelen, maar Łukasiewicz plaatst ze ervoor. Om de stapel zo efficiënt mogelijk
te gebruiken hebben we deze notatie omgekeerd, wij zetten de operators achter de
getallen. Vandaar de benaming Omgekeerde Poolse Notatie of Reverse Polish
Notation, RPN.
De stapel bestaan uit vier opslaglocaties, registers genaamd, die zich boven elkaar
“bevinden”. Deze registers — ze dragen de namen X, Y, Z en T — kunnen vier
getallen opslaan en manipuleren. Het “oudste” getal bevindt zich in het T- (top)
register. De stapel is het werkgebied voor berekeningen.

2-2 RPN: De automatische geheugenstapel
Het meest “recente” getal bevindt zich in het X–register: dit is het getal dat u in de
tweede regel van het scherm ziet.
Elke register is onderverdeeld in drie delen:
Een echt getal of een 1-D vector zal deel 1 bevatten; deel 2 en deel 3 zullen
in dit geval leeg zijn.
Een complex getal of een 2-D vector zal deel 1 en deel 2 bevatten; deel 3 zal
in dit geval leeg zijn.
Een 3-D vector zal in dit geval deel1, deel 2, en deel 3 bevatten.
Bij het programmeren, wordt de stapel gebruikt om berekeningen uit te voeren, om
tijdelijke resultaten op te slaan, om opgeslagen gegevens (variabelen) tussen
programma’s en subroutines uit te wisselen, om invoer te accepteren en om uitvoer
te geven.
T
Deel3
“Oudste” getal
Deel2
Deel1 0,0000
Z
Deel3
Deel2
Deel1 0,0000
Y
Deel3
Weergegeven
Deel2
Deel1 0,0000
X
Deel3
Weergegeven
Deel2
Deel1 0,0000

RPN: De automatische geheugenstapel 2-3
De registers X en Y staan op het scherm
U ziet steeds het X en Y–register, tenzij
er een menu, een bericht, een
vergelijkingsregel, of een programmaregel wordt weergegeven. U zult wel hebben
opgemerkt dat veel functienamen een x of y
bevatten.
Dat is geen toeval, deze letters verwijzen naar het X– en Y–register. Bijvoorbeeld,
z ( verheft tien in de macht van het getal dat in het X–register staat (het
weergegeven getal).
Het X-register wissen
Drukt u op {(º) dan wordt het X-register altijd
nul. Het wordt ook
gebruikt om deze instructie te programmeren. De toets , daarentegen, is
afhankelijk van de context. Hij maakt het beeld leeg of annuleert het, afhankelijk
van de situatie: Deze werkt alleen als {1(º) wanneer het X-register
wordt weergegeven. a werkt ook als {1(º) wanneer het X-register
wordt weergegeven en
de getalinvoer voltooid is (geen cursor op het scherm).
De stapel bekijken
R¶ (Onmlaag rollen)
Met de toets 9 (omlaag rollen)
kunt u de hele inhoud van de stapel bekijken door
de inhoud omlaag te laten rollen, een register per keer. U kunt de getallen zien als
ze rollen door de x- en y- registers.
Stel dat de stapel de getallen 1, 2, 3, 4 bevat. (Druk op
) Door nu vier keer op 9 te drukken ziet u alle nummers een keer
voorbijkomen. Na vier keer staan ze weer op de oorspronkelijke plaats:
T
1
4
3
2 1
Z
2
1 4
3 2
Y
3
2 1
4
3
X
4
3 2
1 4

2-4 RPN: De automatische geheugenstapel
Wat er in het X-register was, gaat naar het T-register, de inhoud van het T-register
gaat naar het Z-register enz. Alleen de inhoud van de registers wordt verplaatst, de
registers zelf blijven waar ze zijn, en alleen de inhoud van het X- en Y-register wordt
weergegeven.
Rµ (Omhoog rollen)
De toets {8 (omhoog rollen) doet net zoiets als 9 maar hij “rolt” de inhoud
van de stapel omhoog, een register tegelijk.
De inhoud van het X–register gaat naar het Y-register; wat in het T–register was
gaat naat het X–register enzovoort.
Het X- en Y-register op de stapel verwisselen
Een andere toets die de inhoud van de stapel manipuleert is Z (x verwisselen
met y). Deze toets verwisselt de inhoud van de registers X en Y, terwijl de rest van
de stapel onveranderd blijft. Door twee keer op Z te drukken herstelt u de
oorspronkelijke volgorde van X- en Y registers.
De Z functie wordt voornamelijk gebruikt om de volgorde van de getallen in
een berekening te wisselen.
Bijvoorbeeld, een manier om 9 ÷ (13 × 8) te berekenen:
Druk op yZ p.
Wilt u deze expressie van links naar rechts
uitvoeren, dan wordt het:
yp.
T12341
Z23412
Y34123
X4
{8 1{8 2{8 3{8 4
Opmerking Er zijn niet meer dan vier getallen in de stapel op elk moment-de
inhoud van de T-register (de bovenste register) zal verloren gaan
als er een vijfde getal wordt ingevoerd.

RPN: De automatische geheugenstapel 2-5
Rekenen - Hoe de stapel het doet
De inhoud van de stapel gaat automatisch op en neer als er nieuwe getallen in het
X-register komen (de stapel optillen) en als een operator twee getallen in het X- en Y-
register combineert naar een nieuw getal in het X-register (de stapel laten zakken).
Stel dat de stapel gevuld is met de getallen 1, 2, 3, en 4. Hier ziet u hoe de inhoud
van de stapel op en neer beweegt tijdens de berekeningen
1. De inhoud van de stapel “valt”. Het T-register wordt gedupliceerd.
2. De inhoud van de stapel wordt “opgetild”. De inhoud van het T-register gaat
verloren.
3. De inhoud van de stapel valt.
Word de inhoud van de stapel opgetild, dan gaat de inhoud van het T-
register verloren. De oude inhoud van het Z-register gaat naar het T-register.
U ziet dat de stapel beperkt is tot vier getallen.
Doordat de stapel automatisch op en neergaat, is het niet nodig het X-regster
leeg te maken voor een nieuwe berekening.
De meeste functies zorgen ervoor dat de inhoud van de stapel wordt opgetild
als er een nieuw getal in het X-register wordt ingevoerd. Zie aanhangsel B
voor een lijst van functies die het optillen van de stapel verhinderen.

2-6 RPN: De automatische geheugenstapel
Hoe ENTER werkt
U weet al dat wordt gebruikt om twee getallen te scheiden die na elkaar
worden ingevoerd. Hoe werkt dat op de stapel? Stel dat de waarden 1, 2, 3 en 4
op de stapel staan. Voer nu twee nieuwe getallen in:
1. De inhoud van de stapel wordt opgetild.
2. Tilt de stapel op en dupliceert het X–register.
3. De inhoud van de stapel wordt niet opgetild.
4. De inhoud van de stapel valt en het T–register wordt gedupliceerd.
dupliceert de inhoud van het X–register in het Y–register. Het volgende
getal dat u invoert (of oproept) overschrijft de kopie van het eerste getal in het X–
register. Het effect is dat de twee ingevoerde getallen gescheiden blijven.
U kunt het dupliceereffect van gebruiken om de stapel snel leeg te maken.
Druk op 0 . Alle registers van de stapel bevatten nu nul.
Nodig is het echter niet voordat u een nieuwe berekening begint.
Een getal twee keer gebruiken
Doordat een nummer kopieert, kunt u deze toets ook voor andere doelen
gebruiken. Om een getal bij zichzelf op te tellen, gebruikt u .
5+6
1 gaat verloren 2 gaat verloren
T1 2 3 3 3
Z2 3 4 4 3
Y3 4 5 5 4
X4
55611
1234

RPN: De automatische geheugenstapel 2-7
De stapel met een constante vullen
kopieert een nummer, en het laten zakken van de stapel eveneens (van T
naar Z). Hierdoor kunt u de stapel gemakkelijk met een numerieke constante vullen
voor berekeningen.
Voorbeeld:
U hebt een bacteriecultuur met een groeisnelheid van 50% per dag. Hoe groot is
een populatie van 100 na drie dagen?
1. Vul de stapel met de groeisnelheid.
2. Geef de oorspronkelijke populatie op.
3. Berekent de populatie na 1 dag.
4. Berekent de populatie na 2 dagen.
5. Berekent de populatie na 3 dagen.
Hoe wordt de stapel leeggemaakt
Maakt u het X-register leeg, dan komt er nul in het X-register. Het volgende getal dat
u invult (of oproept) komt in de plaats van deze nul.
Er zijn vier manieren om de inhoud van het X–register leeg te maken, dat betekent,
voor het leegmaken van x:
1. Druk op
2. Druk op a
3. Druk op {(º) (Vooral gebruikt bij het invoeren van een
programma.)
4. Druk {( !) voor het leegmaken van X-, Y-, Z-, en T-registers
tot nul.
Herhaalt T-register
T 1,5 1,5 1,5 1,5 1,5
Z 1,5 1,5 1,5 1,5 1,5
Y1,5
1,5 1,5 1,5 1,5
X1,5 100y150 y225 y337,5
12345

2-8 RPN: De automatische geheugenstapel
Bijvoorbeeld, u wilde 1 en 3 invoeren, maar u hebt bij vergissing 1 en 2 ingevoerd.
Zo verbetert u de fout:
1. Tilt de stapel op
2. Tilt de stapel op en dupliceert het X-register.
3. Overschrijft het X-register.
4. Maakt het x
leeg door er een nul in te zetten.
5. Overschrijft x
(vervangt de nul.)
Het register LAST X
Het register LAST X hoort bij de stapel. Het bevat het getal dat zich in het X–register
bevond voor de laatste numeriek functie werd uitgevoerd. (Een numerieke functie is
een bewerking die een resultaat produceert uit een of meer andere getallen, zoals
<.) Drukt u op { dan komt deze waarde terug in het X–register.
Deze mogelijkheid om “last x” terug te halen heeft twee toepassingen:
1. Fouten verbeteren.
2. Een getal opnieuw gebruiken in een berekening.
In aanhangsel B ziet u een lijst van functies die x in het register LAST X opslaan.
T
Z
Y1 111
1X1122C033
12345
RPN: De automatische geheugenstapel 2-9
Fouten verbeteren met LAST X
Verkeerde Enkele Argument Functie
Als u de verkeerde enkele argument functie uitvoert, gebruik { om het
getal terug te roepen, zodat u de correcte functie kan uitvoeren. (Druk eerst als
u het onjuiste resultaat van de stapel wilt wissen).
Doordat {P en zS de stapel niet laten zakken, kunt u van deze
functies herstellen op dezelfde manier als met de enkele argument functies.
Voorbeeld:
U berekende zo juist 4,7839 × (3,879 × 105) en u wilt van het resultaat de
vierkantswortel berekenen. Per ongeluk drukt u op *. U hoeft niet opnieuw te
beginnen! Voor het juiste antwoord drukt u op {<.
Fouten met Twee Argument Functies
Als u een fout maakt met een twee argument bewerking (zoals , ), of x),
kunt u het veranderen met { en het omgekeerde van de twee argument
bewerking.
1. Druk op { om het tweede getal terug te roepen (x
voordat u de fout
maakte).
2. Voer de inverse functie uit. Hiermee krijgt u het oorspronkelijke getal terug. Het
tweede getal staat nog steeds in LAST X register. Doe nu dit:
Als u de verkeerde functie heeft gebruikt, Druk dan opnieuw {
om de originele stapelinhoud terug te roepen. Voer nu de correcte functie
uit.
Als u het verkeerde tweede getal hebt gebruikt, toetst dan het juiste in en
voer de functie uit.
Als u het verkeerde eerste getal hebt gebruikt, toets dan het juiste eerste getal in,
druk { om het tweede getal terug te roepen, en voer de functie opnieuw
uit. (Druk eerst als u het onjuiste resultaat van de stapel wilt leegmaken.)

2-10 RPN: De automatische geheugenstapel
Voorbeeld:
U hebt een fout gemaakt in de berekening van
16 × 19 = 304
Er kunnen drie soorten fouten worden gemaakt:
Getallen opnieuw gebruiken met LAST X
U kunt { gebruiken om een getal (zoals een constante) opnieuw te
gebruiken in een berekening. Denk eraan dat u de constante als tweede getal
invoert, vlak voordat u de berekening uitvoert, zodat de constante het laatste getal
is in het X–register. Alleen dan wordt het opgeslagen in LAST X en kan het met
{ worden teruggehaald.
Voorbeeld:
Bereken
Verkeerde
berekening:
Fout: Correctie:
Verkeerde functie {Ù
{y
y
Verkeerd eerste getal {y
y
Verkeerd tweede getal {p y

RPN: De automatische geheugenstapel 2-11
Voorbeeld:
Twee dichtbijstaande sterren zijn Alpha Centauri (op 4,3 lichtjaar afstand) en Sirius
(8,7 lichtjaar). Gebruik c, de lichtsnelheid (9,5 × 1015 meter per jaar) om de
afstanden naar deze sterren te converteren naar meters:
Naar Alpha Centauri: 4,3 jaar × (9,5 × 1015 m/jaar).
Naar Sirius: 8,7 jaar × (9,5 × 1015 m/ jaar).
Invoer: Weergave: Omschrijving:
) Voert het eerste getal in.
) Tussenresultaat.
{ ) Herstelt het scherm van voor
.
p) Eindresultaat.

2-12 RPN: De automatische geheugenstapel
Kettingberekeningen met RPN
Dank zij RPN en het automatische optillen en laten zakken van de stapel kunt u
tussenresultaten bewarenzonder dat u ze hoeft op te slaan of opnieuw hoeft in te
voeren, en zonder haakjes.
Werken vanuit de haakjes
Bijvoorbeeld, bereken (12 + 3) × 7.
Zou u dit op papier uitrekenen, dan berekent u eerst het tussenresultaat (12 + 3) …
(12 + 3) = 15
… en daarna vermenigvuldigt u het tussenresultaat met 7:
(15) × 7 = 105
Bereken de expressie op dezelfde manier in de HP 35s, beginnend van binnen de
haakjes.
U hoeft niet op te drukken om het tussenresultaat op te slaan voordat u
verder gaat. Het is een berekend
resultaat en wordt automatisch opgeslagen.
Invoer: Weergave: Omschrijving:
) Lichtjaren naar Alpha Centauri.
` )_Lichtsnelheid, c.
y) Meters naar Alpha Centauri.
{ ) Haalt c terug.
y) Meters naar Sirius.
Invoer: Weergave: Omschrijving:
) Berekent eerst het tussenresultaat.
RPN: De automatische geheugenstapel 2-13
Bestudeer nu de volgende voorbeelden. Denk eraan dat u alleen gebruikt
om apart ingevoerde getallen te scheiden, bijvoorbeeld bij het begin van een
expressie. De bewerkingen zelf (, , etc.)
scheiden de volgende getallen en
slaan de tussenresultaten op. Het laatste resultaat dat is opgeslagen, is het eerste
dat wordt gebruikt in de volgende berekening.
Bereken 2 ÷ (3 + 10):
Bereken4 ÷ [14 + (7 × 3) – 2] :
Sommen met meerdere haakjes kunnen op dezelfde manier worden opgelost
dankzij de automatische opslag van tussenresultaten. Zou u (3 + 4) × (5 + 6) op
papier oplossen, dan berekent u eerst (3 + 4). Daarna berekent u (5 + 6). Tenslotte
vermenigvuldigt u de twee tussenresultaten om het antwoord te krijgen.
Met de HP 35s werkt u op dezelfde manier door het probleem. U hoeft alleen de
tussenresultaten niet op te schrijven—de rekenmachine onthoudt ze voor u.
Invoer: Weergave: Omschrijving:
y ) Als u op de functietoets drukt, verschijnt
het antwoord. Het resultaat kan in
verdere berekeningen worden gebruikt.
Invoer: Weergave: Omschrijving:
) Berekent eerst (3 + 10).
Zp ) Zet 2 vóór
13 zodat de deling het
juiste resultaat oplevert: 2 ÷ 13.
Invoer: Weergave: Omschrijving:
y ) Berekent (7 × 3).
) Berekent de noemer.
Z ) Zet 4 vóór
33 ter voorbereiding op
de deling.
p) Berekent 4 ÷ 33, het antwoord.
Invoer: Weergave: Description:
) Berekent eerst (3+4)
) Berekent (5+6)

2-14 RPN: De automatische geheugenstapel
Oefeningen
Bereken:
Oplossing:
y <p
Bereken:
Oplossing:
y<
y<
Bereken:
(10 – 5) ÷ [(17 – 12) × 4] = 0,2500
Oplossing:
y Z p
of
y p
Volgorde van berekening
We adviseren u een kettingberekening uit te voeren door te beginnen met de
binnenste haakjes. U kunt echter ook van links naar rechts werken.
Bijvoorbeeld, u hebt dit al uitgerekend:
y) Vermenigvuldigt de tussenresultaten
en geeft het uiteindelijke antwoord.

RPN: De automatische geheugenstapel 2-15
4 ÷ [14 + (7 × 3) – 2]
door met de binnenste haakjes te beginnen (7× 3) en naar buiten te werken, net als
wanneer u met potlood en papier werkt. U drukte op de toetsen
yZ p.
Werkt u van links naar rechts, dan wordt het
yp.
Hiervoor moet u een extra toets indrukken. U ziet dat het eerste tussenresultaat nog
steeds de waarde tussen de binnenste haakjes is (7 × 3). Door van links naar rechts
te werken, hebt u Z niet nodig om de operanden van niet-commutatieve
functies te verwisselen ( en p).
De eerste methode (beginnen met de binnenste haakjes) heeft echter vaak de
voorkeur omdat:
Er minder toetsen nodig zijn.
Er minder ruimte in de stapel nodig is.
Het voorbeeld hierboven heeft, als u van links naar rechts
werkt, op een zeker
moment alle registers in de stapel nodig:
Opmerking Werkt u van links naar rechts, denk er dan aan dat er op ieder
moment niet meer dan vier tussenresultaten mogen zijn. De stapel
heeft ruimte voor vier getallen.
Invoer: Weergave: Omschrijving:
) Zet 4 en 14 als tussenresultaten op
de stapel.
_ Nu is de stapel vol met getallen.
y) Tussenresultaat.
) Tussenresultaat.
) Tussenresultaat.

2-16 RPN: De automatische geheugenstapel
Meer oefeningen
Oefen met het gebruik van RPN door de volgende problemen op te lossen:
Bereken:
(14 + 12) × (18 – 12) ÷ (9 – 7) = 78,0000
A Oplossing:
y p
Bereken:
232 – (13 × 9) + 1/7 = 412,1429
A Oplossing:
{:y3
Bereken:
Oplossing:
y0Z
p<
of
y0
p <
Bereken:
p) Eindresultaat.

Gegevens in variabelen opslaan 3-1
3
Gegevens in variabelen opslaan
De HP 35 s heeft een 30 KB geheugen, in welke u getallen, vergelijkingen, en
programma’s kan opslaan. Getallen kunnen worden opgeslagen in locaties die
variabelen heten, elke heeft een naam met een letter van A tot Z. (U kunt de letter
kiezen om u eraan te herinneren wat daar is opgeslagen, zoals B voor bankbalans
en C voor de snelheid van het licht.)
Voorbeeld:
Dit voorbeeld toont u hoe u de waarde 3 kunt opslaan in de variabele A, eerst in
de RPN stand en dan in ALG stand.
Invoer: Weergave: Omschrijving:
9( )Verander in RPN stand (indien nodig)
)
_
Voer de waarde (3) in
{H !_Het opslagcommando vraagt om een
letter; let op de A…Z annunciator.
A
)
)
De waarde 3 is opgeslagen A en
keert terug naar de stapel.
9( )
)
Verander in ALG stand (indien nodig)
{HA_Opnieuw, het Opslag commando
vraagt om een letter en de A…Z
annunciator verschijnt.
)
De waarde 3 is opgeslagen in A en
het resultaat is geplaatst in regel 2.

3-2 Gegevens in variabelen opslaan
In de ALG stand, kunt u een expressie opslaan in een variabele; in dit geval, wordt
de waarde van de expressie opgeslagen in de variabele in plaats van de expressie
zelf.
Voorbeeld:
Elke roze letter is gecombineerd met een toets en een unieke variabele. (De A..Z
annunciator in het scherm bevestigt dit).
De variabelen, X, Y, Z en T zijn niet hetzelfde als de vier registers: X-register, Y-
register, Z-register en T-register in de stapel.
Getallen opslaan en oproepen
Getallen en vectoren worden opgeslagen in, en opgeroepen van, geletterde
variabelen met behulp van de Opslag ({H) en de Oproep (K)
commando’s. Getallen kunnen echt of complex zijn, decimaal of breuk, basis 10 of
anderen ondersteund door de HP 35s.
Een kopie van het weergegeven getal (X-register) in een directe variabele opslaan:
Druk op {H lettertoets .
De inhoud van een directe variabele terugroepen in het scherm:
Druk op K lettertoets .
Voorbeeld: getallen opslaan.
Sla het getal van Avogadro (ongeveer 6,0221 × 1023 ) op in A.
Invoer: Weergave: Omschrijving:
p
{H
-ª
)
Voer de expressie in, ga dan
door zoals in het vorige
voorbeeld.
Gegevens in variabelen opslaan 3-3
Om een waarde opgeslagen in een variabele terug te roepen, gebruik het Recall
commando. De weergave van dit commando is een beetje anders dan van RPN tot
ALG stand, zoals het volgende voorbeeld laat zien.
Voorbeeld:
In dit voorbeeld, roepen we de waarde op van 1,75 dat we hebben opgeslagen in
de variabele G in het laatste voorbeeld. Dit voorbeeld neemt aan dat HP 35s nog
steeds in de ALG stand staat van het begin.
In de ALG stand, kan oproepen gebruikt worden om een variabele te plakken in
een expressie in de commando regel. Stel dat we 15-2×G willen berekenen, met
G=1,75 van hierboven.
We gaan nu door in de RPN stand en roepen de waarde van G op.
Invoer: Weergave: Omschrijving:
`
)_Getal van Avogadro.
{HA)_“” vraagt om een variabele.
)
)
Een kopie van het getal van
Avogadro wordt opgeslagen in A. De
getalinvoer wordt hiermee beëindigd.
_ Maakt de waarde op het scherm
leeg.
KA..Z De A..Z annunciator gaat aan
A/
)
Het getal van Avogadro wordt van A
naar het scherm gekopieerd.
Invoer: Weergave: Omschrijving:
KG
)
Het indrukken van K activeert de
A…Z stand; geen commando is
geplakt in regel 1.
Invoer: Weergave: Omschrijving:
y
KG
.h
)

3-4 Gegevens in variabelen opslaan
Een variabele bekijken
Het VIEW (bekijken) commando (z) geeft de waarde van een variabele
weer zonder deze waarde terug te roepen uit het x-register. Het scherm neemt deze
vorm aan Variabele=Waarde. Als het getal teveel cijfers heeft om in het scherm te
passen, gebruik dan {Õ of {Ö om de gemiste cijfers te zien. Om de
VIEUW weergave te beïndigen, druk a of . Het VIEW commando wordt het
meest gebruikt in programmeren maar het is ook nuttig elke keer dat u een waarde
van een variabele wilt bekijken zonder de stapel te beïnvloeden.
De MEM Catalogus gebruiken
De MEMORY (GEHEUGEN) catalogus (zu) verschaft informatie over het
beschikbare geheugen. De catalogus weergave heeft het volgende formaat:
)# )
QQQ PP8PPP
waar mm,mmm is het aantal bytes van het beschikbare geheugen en nnn is de
hoeveelheid gebruikte indirecte variabelen.
Voor meer informatie over indirecte variabelen, zie Hoofdstuk 14.
De VAR catalogus
Standaard bevatten alle variabelen van A tot Z de waarde nul. Als u een niet-nul
waarde in elke directe variabele opslaat, kan de waarde van die variabele worden
bekeken in de VAR catalogus (zu(#)).
Invoer: Weergave: Omschrijving:
9()Verander in RPN stand
K
_
In de RPN stand, plakt Khet
commando in de bewerkingsregel.
G)
)
Op hoeft niet gedrukt te
worden.

Gegevens in variabelen opslaan 3-5
Voorbeeld:
In dit voorbeeld, slaan we 3 op in C, 4 in D, en 5 in E. Dan gaan we deze
variabelen bekijken via de VAR catalogus en ze ook leegmaken. Dit voorbeeld
gebruikt de RPN stand.
Let op dat de © en ª annunciators aangeven dat de Ø en × toetsen aktief
zijn om u te helpen door de catalogus te scrollen; maar als de Breuk stand aktief is,
zullen de c en d annunciators niet accuraat aangeven tenzij er maar een
variabele in de catalogus zit. We keren terug naar ons voorbeeld, om te laten zien
hoe je door de VAR catalogus moet navigeren.
Terwijl we in de VAR catalogus zijn, laten we doorgaan met dit voorbeeld om u te
laten zien hoe een waarde van een variabele tot nul te wissen, effectief verwijderen
van de huidige waarde. We verwijderen E.
Stel dat u de waarde van C wilt kopiëren naar de stapel.
Invoer: Weergave: Omschrijving:
{(#
)
Alle directe variabelen wissen
{HC
{HD
{HE
Slaat 3 op in C, 4 op in D en 5 op in
E.
zu(#)/
Voer de VAR catalogus in.
Ø/
Scroll omlaag naar de volgende
directe variabele met niet-nul
waarde : D=4.
Ø/
Scroll nog een keer omlaag om E=5
te zien.
{/
E is niet meer in de VAR catalogus,
aangezien zijn waarde nul is. De
volgende variabele is C als
aangegeven.
De waarde van C=3 is gekopiëerd
naar het x-register en 5 (voorheen
bepaals als E=5) wordt verplaatst
naar het y-register.

3-6 Gegevens in variabelen opslaan
Om de VAR catalogus op elk moment te verlaten, druk @ of . Een andere
methode om een variabele te wissen is om de nulwaarde erin op te slaan.
Uiteindelijk, kunt u alle directe variabelen leegmaken door {
(# )te drukken. Als alle directe variabelen de waarde nul hebben, zal een
poging om naar de VAR catalogus te gaan de foutmelding “ # / ”
weergeven.
Als de waarde van een variabele teveel cijfers heeft om geheel weer te geven, kunt
u Õ en Ö gebruiken om de gemiste cijfers te bekijken.
Rekenen met opgeslagen variabelen
Rekenen met opslaan en rekenen met oproepen maken het mogelijk berekeningen
uit te voeren met een getal dat in een variabele opgeslagen is, zonder dat het
nodig is de variabele in de stapel op te roepen. Een berekening gebruikt een getal
uit het X-register en een waarde uit de gewenste variabele.
Reken met opslag
Rekenen met opslag gebruikt {H, {H, {Hy, of
{H p om berekeningen uit te voeren in de variabele zelf en het resultaat
daar op te slaan. Het gebruikt de waarde in het X-register en heeft geen invloed op
de stapel.
Nieuwe waarde van een variabele = Vorige waarde van de variabele {+, –, ×, ÷} x.
Bijvoorbeeld, u wilt de waarde in A(15) verminderen met de inhoud van het X-
register (3, wordt getoond). Druk op {HA. Nu is A = 12, terwijl er
nog steeds 3 op het scherm staat.

Gegevens in variabelen opslaan 3-7
Rekenen met oproepen
Rekenen met oproepen gebruikt K, K, Ky of Kp voor
het rekenen in het X-register met gebruik van een opgeroepen nummer en om het
resultaat op het scherm achter te laten. Alleen het X-register wordt beïnvloed. De
waarde in de variabele blijft hetzelfde en het resultaat vervangt de waarde in het x-
register.
Nieuwe x = Vorige x {+, –, ×, ÷} variabele
Bijvoorbeeld, u wilt het getal in het X-register (3, wordt getoond) delen door de
waarde in A(12). Druk op K p A. Nu is x = 0,25, terwijl er nog steeds 12 in
A staat. Deze wijze van rekenen spaart geheugen in het programma: K A
(één instructie) gebruikt half zo veel geheugen als as K A, (twee
instructies).
A15 A12 Resultaat: 15 – 3
dat is, A – x
TtTt
ZzZz
YyYy
X3{HAX3
A12 A12
TtTt
ZzZz
YyYyResultaat: 3 ÷ 12
dat is, x ÷ 12
X3KpAX0.25

3-8 Gegevens in variabelen opslaan
Voorbeeld:
Stel dat de variabelen D, E en F de waarden 1, 2 en 3 bevatten. Op de volgende
manier kunt u 1 bij elk van deze variabelen optellen.
Na het laatste voorbeeld bevatten D E, en F de waarden 2, 3 en 4. Deel D door 3,
vermenigvuldig het met E, en tel er F bij op.
Een variabele met x verwisselen
Met de toets z Y kunt u de inhoud van x (het weergegeven X-register)
verwisselen met de inhoud van een variabele. Deze functie heeft geen invloed op
het Y-, Z- en T-register.
Invoer: Weergave: Omschrijving:
{HD
{HE
{HF
)
)
)
Slaat de beginwaarden in de
variabelen op.
{H
D{H
E{H
F
)
Telt 1 op bij D, E en F.
zD/
)
Toont de huidige waarde van D.
zE/
)
zF/
)
a) Annuleert de weergave van de
variabele, zodat het X-register weer
wordt getoond.
Invoer: Weergave: Omschrijving:
KpD) Berekent 3 ÷ D.
KyE) 3 ÷ D × E.
KF) 3 ÷ D × E + F.

Gegevens in variabelen opslaan 3-9
Voorbeeld:
De variabele “I” en “J”
Er zijn twee variabelen waar u direkt toegang tot heeft; de variabelen I en J.
Hoewel ze waarden opslaan net als andere variabelen, zijn I en J speciaal omdat
ze gebruikt kunnen worden voor referentie naar andere variabelen, inclusief de
statische registers, met gebruik van de (I) en (J) commando’s. (I) is terug te vinden
op de toets, en (J) op de toets. Dit is een programmeringstechniek die
indirecte addressering wordt genoemd die besproken wordt in “ Indirect
Addresseren van Variabelen en Labels in hoofdstuk 14.
Invoer: Weergave: Omschrijving:
{H
A
) Slaat 12 in variabele A op.
_Geeft x weer.
zYA) Verwisselt de inhoud van het X-
register met variabele A.
zYA) Verwisselt de inhoud van het X-
register met variabele A.
A12 A3
TtTt
ZzZz
YyYy
X3zYAX12

Functies voor reële getallen 4-1
4
Functies voor reële getallen
Dit hoofdstuk behandelt de meeste functies van de rekenmachine waarmee u
berekeningen kunt uitvoeren op reële getallen, waaronder een aantal numerieke
functies die in programma's worden gebruikt (zoals ABS, de absolute waarde).
Deze functies zijn als volgt in groepen onderverdeeld:
Exponentiële en logaritmische functies.
Quotiënt en rest bij deling.
Machtsverheffen. (0 en z.)
Trigonometrische functies.
Hyperbolische functies.
Percentage-functies.
Natuurkundige constanten
Conversiefuncties voor coördinaten, hoeken en eenheden.
Waarschijnlijkheidsfuncties.
Delen van getallen (functies om getallen te veranderen).
Aritmetische functies en berekeningen zijn behandeld in hoofdstuk 1 en 2.
Geavanceerde numerieke bewerkingen (vinden van een wortel, integreren,
complexe getallen, conversies naar andere talstelsels en statistieken worden
verderop besproken. De voorbeelden in dit hoofdstuk gaan er vanuit dat de HP 35s
in de RPN stand staat.
Exponentiële en logarithmische functies
Zet het getal in het X-register en voer de functie uit - het is niet nodig op te
drukken.

4-2 Functies voor reële getallen
Quotiënt en rest bij deling
U kunt zJ(!,) en zJ(PGT) gebruiken voor het
maken van gehele quotiënt en rest bij deel, door twee getallen te delen.
1. Toets het eerste getal in.
2. Druk op om de twee getallen van elkaar te scheiden.
3. Toets het tweede getal in. (Druk niet op .)
4. Druk op de functietoets.
Voorbeeld:
Voor het weergeven van quotiënt en de rest geproduceerd door 58 ÷ 9
Machtfuncties
Met RPN berekent u y in de macht x door y x in te toetsen en daarna op
0 te drukken. (Is y > 0, dan kan x ieder rationeel getal zijn, is y < 0, is y < 0,
dan moet x positief zijn.)
Om te berekenen: Drukt u op:
Natuurlijke logaritme (grondtal e){-
Gewone logaritme (grondtal 10) z+
Natuurlijke exponent {*
Gewone exponent (anti-logaritme) z(
Invoer: Weergave: Omschrijving:
z
J(!,)
) Geeft het quotiënt weer.
z
J(PGT)
) Geeft de rest weer.

Functies voor reële getallen 4-3
In de RPN stand berekent u de wortel x van het getal y (de xde wortel van y), door
y x in te typen, gevolgd door z.. Is y < 0, dan moet x een geheel
getal zijn.
Trigonometrie
π invoeren
Druk op z M om de eerste 12 cijfers van π in het X-register te zetten.
(Het weergegeven getal hangt af van de weergave formaat). Aangezien zM
een functie is die een benadering van π terugbrengt naar de stapel, is het niet
nodig om op te drukken.
De rekenmachine kan π niet precies bepalen, omdat π een irrationeel getal is.
Om te berekenen: Drukt u op: Resultaat:
152{: )
106z (88)
540 )
2–1,4 _ 0)
(–1,4)3_0 .)
Om te berekenen: Drukt u op: Resultaat:
< )
_z
.
.)
. )
_z.
)
196
3125−
4625
4,1 37893,
−

4-4 Functies voor reële getallen
De hoekmodus
De hoekmodus geeft aan welke eenheid verondersteld moet worden bij het reken
met hoeken in trigonometrische functies. Door de modus te veranderen beïnvloedt u
niet de getallen die al berekend zijn (zie “Conversiefuncties” verderop in dit
hoofdstuk).
360 graden = 2π radialen = 400 grads
Om een hoekmodus te kiezen, drukt u op 9. Er wordt een menu getoond
waarin u een optie kunt selecteren.
Trigonometrische functies
Met x op het scherm:
Option Omschrijving Annunciator
Stelt de gradenstand in, welke decimale
graden gebruikt in plaats van hexadecimale
graden (graden, minuten, seconden)
geen
Stelt radialen in RAD
Stelt helling in GRAD
Om te berekenen: Drukt u op:
Sinus van x.N
Cosinus van x.Q
Tangens van x.T
Arc sinus van x.z L
Arc cosinus van x.z O
Arc tangens van x.z R
Opmerking Berekeningen met het irrationale getal π kunnen niet precies
uitgedrukt worden met de 15-cijferige interne precisie van de
rekenmachine. Dit komt vooral naar voren bij trigonometrie.
Bijvoorbeeld, de berekende sinus van π (radialen) is niet nul
maar –2,0676 x 10–13, dat is een zeer klein getal dat weinig
verschilt van nul.
Functies voor reële getallen 4-5
Voorbeeld:
Toon aan dat de cosinus van (5/7)π radialen overeenkomt met de cosinus van
128,57° (in vier significante cijfers).
Opmerking voor programmeurs:
Vergelijkingen met inverse trigonometrische functies om een hoek θ te bepalen, zien
er vaak zo uit:
θ
= arctan (y/x).
Als x = 0 , is y/x onbepaald, wat een fout als resultaat geeft: # & .
Invoer: Weergave: Omschrijving:
9()Stelt radialen in; de annunciator
RAD verschijnt.
) 5/7 in decimale opmaak.
z M y Q .) Cos (5/7)π.
9().) Stelt graden in (geen
annunciator).
Q
.) Berekent cos 128,57°, dat is
hetzelfde als cos (5/7)π.
4-6 Functies voor reële getallen
Hyperbolische functies
Met x op het scherm:
Percentagefuncties
De percentagefuncties zijn uitzonderlijk (vergeleken met y en p ) omdat ze de
inhoud van het basisgetal (in het Y-register) bewaren als ze het resultaat van een
procentberekening (in het X-register) teruggeven. U kunt daardoor berekeningen
uitvoeren op het basisgetal en het resultaat zonder dat u het basisgetal opnieuw
hoeft in te voeren.
Voorbeeld:
Wat is de BTW van 6% als de prijs exclusief $15,76 is.
Gebruik FIX 2 zodat de weergave correct wordt afgerond voor geldbedragen.
Om te berekenen: Drukt u op:
Hyperbolische sinus of x (SINH). z 7 N
Hyperbolische cosinus of x (COSH). z 7 Q
Hyperbolische tangens of x (TANH). z 7 T
Hyperbolische arc sinus of x (ASINH). z 7{ L
Hyperbolische arc cosinus of x (ACOSH). z 7{ O
Hyperbolische arc tangens of x (ATANH). z 7{ R
Om te berekenen: Drukt u op:
x% of yy x {P
Procentuele verandering van y naar x. (y≠ 0) y x z S

Functies voor reële getallen 4-7
Stel dat het $15,76 objekt het afgelopen jaar $16,12 kostte. Wat is de prijs dan
percentagewijs veranderd met het afgelopen jaar?
Invoer: Weergave: Omschrijving:
z8(%)
Rondt de weergave af op twee
cijfers achter de komma.
)
{P ) Berekent 6% BTW.
) Totale prijs (exclusief plus 6%
BTW).
Invoer: Weergave: Omschrijving:
)
z
S
.) Dit jaar is de prijs 2,2% gezakt
van de prijs van het afgelopen
jaar.
z8(%)
.) Herstelt FIX 4 formaat
Opmerking De volgorde van de twee getallen is belangrijk voor de functie
%CHG. Hierdoor wordt de procentuele verandering positief of
negatief.

4-8 Functies voor reële getallen
Natuurkundige constanten
In het menu CONST vindt u 41 natuurkundige constanten. U vindt ze door op z
te drukken.
Het menu CONST
Object Omschrijving Waarde
FLichtsnelheid in vacuüm 299792458 m s–1
JStandaard zwaartekrachtversnelling 9,80665 m s–2
Gravitatieconstante van Newton 6,673×10 –11 m3 kg– 1s–2
#P Volume van een mol ideaal gas 0,022413996 m3 mol–1
Constante van Avogadro 6,02214199×10 23 mol–1
∞Constante van Rydberg 10973731,5685 m–1
H# Elementaire lading 1,602176462×10–19 C
PH Massa van een elektron 9,10938188×10–31 kg
PR Massa van Planck 1,67262158×10–27 kg
PQMassa van een proton 1,67492716×10–27 kg
P_ Massa van een muon 1,88353109×10–28 kg
NConstante van Boltzmann 1,3806503×10–23 J K–1
KConstante van Planck 6,62606876×10–34 J s
Constante van Dirac (constante van
Planck gedeeld door 2 pi)
1,054571596×10–34 J s
«µQuantum van magnetische flux 2,067833636×10–15 Wb
DµStraal van Bohr 5,291772083×10–11 m
εµElektrische constante 8,854187817×10–12 F m–1
Gasconstante 8,314472 J mol–1 k–1
Constante van Faraday 96485,3415 C mol–1
WConstante van atomische massa 1,66053873×10–27 kg
_µMagnetische constante 1,2566370614×10–6 NA–2
_ Bohr magneton 9,27400899×10–24 J T–1
_ Nucleair magneton 5,05078317×10–27 J T–1
_ Magnetisch moment van een proton 1,410606633×10–26 J T–1
_H Magnetisch moment van een elektron –9,28476362×10–24 J T–1
WQ Magnetisch moment van een neutron –9,662364×10–27 J T–1
K

Functies voor reële getallen 4-9
Een constante invoegen:
1. Zet de cursor op de plek waar de constante moet komen.
2. Druk op z om het menu met constanten te openen.
3. Druk op ÕÖ×Ø (of druk op z om naar de volgende
pagina te gaan, een pagina tegelijk) om door het menu te zoeken tot de
gewenste constante onderstreept is. Druk daarna op om de constante
in te voegen.
Let op dat constanten gerefereerd moeten worden bij hun namen in plaats van hun
waarden, wanneer ze gebruikt worden in expressies, vergelijkingen en
programma’s.
__ Magnetisch moment van een muon –4,49044813×10–26 J T–1
TH Klassieke straal van een elektron 2,817940285×10–15 m
'µKarakteristieke impedantie van vacuum 376,730313461 Ω
λFGolflengte van Compton 2,426310215×10–12 m
λFQ Compton golflengte van een proton 1,319590898×10–15 m
λFR Compton golflengte van een proton 1,321409847×10–15 m
αFijnstructuurconstante 7,297352533×10–3
σConstante van Stefan-Boltzmann 5,6704×10–8 W m–2 K–4
VSmeltpunt van water 273,15
aVP Standaard-atmosfeer 101325 Pa
γRFirst radiation constant 267522212 s–1T–1
Second radiation constant 374177107×10–16 W m2
Tweede stralingsconstante 0,014387752 m K
µConductantiequantum 7,748091696×10–5 S
HGrondgetal van natuurlijk logaritme
(natuurlijke constanten)
2,71828182846
Referentie: Peter J.Mohr en Barry N.Taylor, CODATA Recommended Values of the
Fundamental Physical Constants: 1998, Journal of Physical and Chemical
Reference Data, Vol.28, No.6,1999 en Reviews of Modern Physics, Vol.72,
No.2, 2000.
Object Omschrijving Waarde

4-10 Functies voor reële getallen
Conversiefuncties
De HP 35s ondersteunt 4 soorten conversies. U kunt converteren tussen:
rechthoekige en polaire formaten voor complexe getallen
graden, radialen en hellingen voor hoekmetingen
decimale en hexadecimale formaten voor tijd ( en graden)
verschillende ondersteunde eenheden (cm/in, kg/lb, etc)
Rechthoekige en polaire conversies uitgezonderd, is elke conversie geassociëerd
met een speciale toets. De linker (gele) shift van de toetst converteert op een manier,
terwijl de rechter (blauwe) shift van dezelfde toets de andere converteert. Voor elke
conversie van dit type, wordt het getal dat u heeft ingevoerd gemeten door de
andere eenheid. Bijvoorbeeld, wanneer u ¾ gebruikt om een getal naar
Fahrenheit graden te converteren, moet het nummer dat u invoert een temperatuur
worden gemeten in graden Celsius. De voorbeelden in dit hoofdstuk gebruiken van
de RPN stand. In de ALG stand, voer eerst de functie in, dan het getal dat
geconverteerd moet worden.
Rechthoekige/Polaire Conversies
Poolcoördinaten (r,
θ
) en rechthoekige coördinaten (x,y) worden gemeten zoals in
de afbeelding. De hoek
θ
gebruikt eenheden zoals ingesteld door de huidige
hoekmodus. Een berekend resultaat voor
θ
is tussen –180° en 180°, tussen –π en π
radialen, of tussen –200 en 200 grads.

Functies voor reële getallen 4-11
Converteren tussen rechthoekige en polaire coördinaten:
Het formaat voor de afgebeelde complexe getallen is een modus instelling. U kunt
een complex getal in elk formaat invoeren; na de invoer, wordt het complexe getal
geconverteerd in het formaat dat bepaald wordt door de modusinstelling. Dit zijn
de benodigde stappen voor het instellen van een complex getalformaat:
1. Druk op z8 en kies dan of (º ¸) of (T) in de
RPN stand (in ALG stand, kunt u ook (º-¸ ) kiezen
2. Voer uw gewenste coordinaatswaarde in (x 6 y, x y 6 of r {?
a)
3. Druk op
Voorbeeld: Conversie van polair naar rechthoekig.
Er wordt gevraagd naar de zijden x en y van de linker driehoek en naar de
hypotenusa r en de hoek
θ
van de rechter driehoek.
Invoer: Weergave: Omschrijving:
9()
z8 (º ¸)
Stelt Graden en complexe
coordinaat stand in.
{?
) ) Converteert r
θ
a (polair) naar
xiy (rechthoekig).
y
10
30
o
x
r
4
3
θ

4-12 Functies voor reële getallen
Voorbeeld: Conversie met vectoren.
Ingenieur P.C. Bord heeft vastgesteld dat in het getoonde RC-circuit de totale
impedantie 77,8 ohm is en dat de spanning 36,5° naijlt op de stroom. Wat is de
waarde van weerstand R en capacitieve reactantie XC in het circuit?
Use a vector diagram as shown, with impedance equal to the polar magnitude, r,
Gebruik het getoonde vectordiagram, met een impedantie gelijk aan de polaire
grootte, r, en als hoek,
θ
, de waarde die de spanning naijlt. Worden de waarden
geconverteerd naar rechthoekige coördinaten, dan is x de weerstand R in ohm en y
de reactantie XC in ohms.
z8
(T)
)θ) Stelt complexe coordinaat
stand in.
6 )θ) Converteert xiy (rechthoekig)
naar r
θ
a (polair).
Invoer: Weergave: Omschrijving:
9()
¹8 (º ¸)
Stelt Graden en complexe
coordinaat stand in.
{?
_
)θ.) Geeft
θ
, hoek waarin de
spanning naijlt. Geeft r, de
totale impedantie.
) .) Berekent x, weerstand
in ohm, R.
Berekent y, weerstand
in ohm, XC
R
C
R
Xc
_
36.5
o
77.8 ohms
θ
Functies voor reële getallen 4-13
Tijdconversies
De HP 35s can tussen decimale en hexadecimale formaten voor getallen
converteren. Dit is vooral makkelijk voor tijd en hoeken gemeten in graden.
Bijvoorbeeld, in decimaal formaat wordt een hoek uitgerekend in graden,
uitgedrukt als D.ddd…, terwijl in hexadecimalen dezelfde hoek wordt uitgedrukt als
D.MMSSss, waar D het gehele deel is van de gemeten graad, is ddd...het
gebroken deel van de graadmeting, MM is het gehele deel van minuten, SS het
gehele getal in seconden en ss het gebroken deel van het getal in seconden.
Converteren tussen decimale formaten en uren, minuten en seconden:
1. Voer het getal in dat u wilt converteren
2. Druk zt voor het converteren van uren/graden, minuten, en
seconden of druk {5 om terug te converteren naar decimaal formaat.
Voorbeeld: Conversie van tijd.
Hoeveel minuten en seconden zijn er in 1/7 van een uur? Gebruik FIX 6 voor het
antwoord.
Hoekconversies
Converteert u naar radialen, dan wordt verondersteld dat er graden in het x-register
staan. Converteert u naar graden, dan wordt verondersteld dat er radialen in het x-
register staan.
Invoer: Weergave: Omschrijving:
z8(%)
Stelt FIX 6 weergave formaat in.
)
+
1/7 uur als decimale breuk.
{ t)
)
Komt overeen met 8 minuten en
34,29 seconden.
z8(%)
)
)
Herstelt FIX 4 formaat
4-14 Functies voor reële getallen
Een hoek converteren tussen graden en radialen:
Voorbeeld
In dit voorbeeld, converteren we een hoekmeeting van 30° naar π/6 radialen.
Eenheidsconversies
De Hp 35s heeft tien eenheid-conversiefuncties op het toetsenbord:: kg, lb,
ºC, ºF, cm, in, l, gal, MILE,KM
Invoer: Weergave: Omschrijving:
)
_
Voer de hoek in graden in.
zµ)
)
Converteer naar radialen. Lees het
resultaat als 0,5236, een decimale
benadering van π/6.
Om: Naar: Drukt u op: Displayed Results:
1 lb kg {} ) (kilogram)
1 kg lb z| ) (engels pond)
32 ºF ºC {~ ) (°C)
100 ºC ºF z ) (°F)
1 in cm { ) (centimeter)
100 cm in z ) (inch)
1 gal l { ) (liter)
1 l gal z ) (gallon)
1 MILE KM {<)(KMS)
1 KM MILE z;)(MILES)

Functies voor reële getallen 4-15
Waarschijnlijkheidsfuncties
Faculteit
Om de faculteit van een niet-negatief geheel getal x te berekenen, (0 ≤ x ≤ 253),
drukt u op { * (met rechterhift 6).
Gamma
Om de gammafunctie van een gebroken getal te berekenen x, Γ(x), key in (x – 1)
en drukt u op { *. De functie x! berekent Γ(x + 1). De waarde van x kan niet
een negatief geheel getal zijn.
Waarschijnlijkheid
Combinaties
Om het aantal mogelijke verzamelingen van n objecten te bepalen waarvan u er r
tegelijk neemt, toetst u eerst n in, z x, en daarna r (alleen niet negatieve
gehele getallen). Geen object kan meer dan eens in een verzameling voorkomen
en verschillende volgordes van dezelfde r objecten gelden niet als verschillend.
Permutaties
Om het aantal mogelijke indelingen van n objecten te bepalen waarvan u er r
tegelijk neemt, toetst u eerst n in, {{, en daarna r (alleen niet negatieve
gehele getallen). Geen object kan meer dan eens in een indeling voorkomen en
verschillende volgordes van dezelfde r objecten gelden als verschillend.
Seed
Om het getal in x te gebruiken als nieuwe seed voor de generator van willekeurige
getallen, drukt u op z h.
Willekeurige getallen
Om een willekeurig getal te genereren in het bereik 0 < x < 1, drukt u op {
j. (Het resultaat wordt berkend door een uniform gedistribueerde pseudo-
randomgenerator. Het voldoet aan de spectraal test van D. Knuth, The Art of
4-16 Functies voor reële getallen
Computer Programming, vol. 2, Seminumerical Algorithms, vol. 2, London: Addison
Wesley, 1981.)
De RANDOM-functie gebruikt een seed om een willekeurig getal te genereren.
Ieder getal wordt vervolgens de seed voor het volgende getal. Een reeks
willekeurige getallen kan dus herhaald worden door steeds met dezelfde seed te
beginnen. U kunt een nieuwe seed opgeven met de functie SEED. Wordt het
geheugen schoongemaakt, dan wordt de seed nul gemaakt. Is de seed nul, dan
genereert de rekenmachine zelf een seed.
Voorbeeld: Combinaties van personen.
Een bedrijf dat 14 vrouwen 10 mannen in dienst heeft, vormt nu een
veiligheidscommissie bestaande uit zes personen. Hoeveel verschillende
combinaties van mensen zijn er mogelijk?
Worden de medewerkers willekeurig gekozen, hoe groot is dan de kans dat de
commissie uit zes vrouwen bestaat? Om de waarschijnlijkheid van zo’n gebeurtenis
te vinden, delen we het aantal combinaties dat eraan voldoet door het totaal aantal
cominaties.
Invoer: Weergave: Omschrijving:
_
Vierentwintig personen waarvan
er zes tegelijk gegroepeerd
worden.
z x8) Totaal aantal mogelijke
combinaties.
Invoer: Weergave: Omschrijving:
_
Uit veertien personen worden er
zes tegelijk gekozen.
z x8) Aantal combinaties van zes
vrouwen in de commissie.
Z8) Totaal aantal combinaties terug in
het X-register.
p) Deelt combinaties met alleen
vrouwen door het totaal aantal.
Het resultaat is de
waarschijnlijkheid dat een
combinatie alleen uit vrouwen
bestaat.

Functies voor reële getallen 4-17
Delen van getallen
Deze functies worden voornamelijk bij programmering gebruikt.
Het gehele deel
Om het deel achter de komma van x te verwijderen en te vervangen door nul, drukt
u op zJ (). (Bijvoorbeeld, het getal 14,2300 verandert dan in
14,0000.)
Het gebroken deel
Om het deel vóór de komma van x te verwijderen en door nul te vervangen, drukt u
op zJ (). (Bijvoorbeeld, het gebroken deel van 14,2300 is
0,2300)
Absolute waarde
Om een getal te vervangen in het x-register met zijn absolute waarde, druk op {
A. Voor complexe getallen en vectoren, is de absolute waarde van:
1. een complex getal in in rθa formaat is r
2. een complex getal in in xiy formaat is
3. een vector [A1,A2,A3, …An] is =
Argument waarde
Om het argument van een complex getal te bepalen, gebruik z=. Het
argument van een complex getal:
1. in rθa formaat is a
2. in xiy formaat is Atan(y/x)
Teken
Om het teken van x te bepalen, drukt u op zJ( ). Is x negatief,
dan verschijnt er –1,0000; if x nul, dan wordt het 0,0000; en is x positief, dan
verschijnt er 1,0000.
22 yx +
A22
2
2
1n
AAA +⋅⋅⋅++
4-18 Functies voor reële getallen
Grootste gehele getal
Om het grootste gehele getal te vinden dat niet groter is dan x, drukt u op
zJ (!).
Voorbeeld:
Dit voorbeeld somt veel van de bedieningen op dat delen van getallen bepaald.
De functie ({ I ) rondt x intern af tot het aantal cijfers dat bepaald wordt
door de weergave op het scherm. (Intern wordt een getal voorgesteld door 12
cijfers.) Zie hoofdstuk 5 voor het gedrag van RND bij het weergeven van een breuk.
Om te berekenen: Drukt u op: Weergave:
Het gehele deel van 2,47 zJ ())
Het gebroken deel van 2,47 zJ ())
De absolute waarde van –7 _{ A)
Het teken van 9 zJ ( ))
Het grootste gehele getal dat
niet meer is dan –5,3
_zJ
(!)
.)

Breuken 5-1
5
Breuken
In hoofdstuk 1, werd in het gedeelte breuken de beginselen van
invoeren,weergeven en rekenen met breuken geïntroduceerd. Dit hoofdstuk geeft
meer informatie over deze onderwerpen. Hier is een kort overzicht over het
invoeren en weergeven van breuken:
Om een breuk in te voeren, druk tweemaal op : eenmaal achter het
gehele deel van een gemengd getal en opnieuw tussen de teller en noemer
van het gebroken deel van het getal. Voor het invoeren van 2 3/8, druk op
. Voor het invoeren van 5/8, druk of op of
.
Om de Breuk weergave aan en uit te zetten, druk {. Wanneer de
Breuk-weergave modus is uitgezet, refereert het scherm aan de vorige
weergave set via het weergavemenu. Kiezen van een formaat via dit menu zet
ook de Breuk- weergave modus uit, als het aktief is.
Functies werken hetzelfde met breuken als met gewone decimale getallen —
met uitzondering van RND, dat later in dit hoofdstuk wordt besproken.
De voorbeelden in dit hoofstuk gebruiken allemaal RPN tenzij anders aangegeven.
Breuken invoeren
Bijna ieder getal kunt u ook als breuk invoeren — zelfs een ontaarde breuk, waarin
de teller groter is dan de noemer.
Voorbeeld:
Invoer: Weergave: Omschrijving:
{ Zet de weergave van breuken aan.
+ Invoer van 1,5; getoond als breuk.
+ Invoer van 1 3/4.
{ ) x
wordt als decimaal getal getoond.
{ + x
wordt als breuk getoond.

5-2 Breuken
Als u niet dezelfde resultaten ziet als in het voorbeeld, heeft u misschien per
ongeluk veranderd hoe breuken worden weergegeven. (“De weergave van breuken
veranderen” later in dit hoofdstuk.)
Hierna geven we meer voorbeelden van geldige en ongeldige breuken.
Breuken op het scherm
Hebt u de rekenmachine ingesteld om breuken weer te geven, dan wordt een getal
intern nog steeds opgeslagen als een decimaal getal, maar het wordt weergegeven
als een breuk, zo nauwkeurig mogelijk. Verder ziet u annunciators die de richting
tonen van de onnauwkeurigheid van de breuk, vergeleken met de decimale waarde
van 12 cijfers. (De meeste statistische registers zijn uitzonderingen — deze worden
altijd decimaal getoond.)
Regels voor de weergave
De breuk die u ziet, kan anders zijn dan de breuk die u invoert. De
standaardinstelling is dat de rekenmachine een breuk toont volgens de volgende
regels. (Hoe u de regels verandert, leest u in “De weergave van breuken
veranderen” verderop in dit hoofdstuk.)
Het getal heeft een geheel deel en zonodig een breuk waarin (de noemer
minder is dan de teller).
De noemer is niet groter dan 4095.
De breuk is zo ver mogelijk vereenvoudigd.
Voorbeelden:
Hier volgen voorbeelden van waarden die u opgeeft, en de weergegeven
resultaten. Ter vergelijking ziet u ook de 12-cijferige interne waarde. De
annunciators c en d in de laatste kolom worden hieronder uitgelegd.

Breuken 5-3
Nauwkeurigheidsannunciators
De nauwkeurigheid van een weergegeven breuk blijkt uit de annunciators c en d
rechts in het scherm. De rekenmachine vergelijkt de waarde van het interne
12-cijferige nummer met de waarde van de getoonde breuk:
Ziet u geen annunciator, dan komt de 12–cijferige waarde precies overeen
met de waarde van de getoonde breuk.
Als u d ziet, is het gebroken deel van de interne 12–cijferige waarde iets
minder dan dat van de weergegeven breuk- de exacte teller is niet meer dan
0,5 minder dan de weergegeven teller.
Als u c ziet, is het gebroken deel van de interne 12–cijferige waarde iets
hoger dan dat van de weergegeven breuk — de exacte teller is niet meer
dan 0,5 meer dan de weergegeven teller.
Hier ziet u hoe de getoonde breuk verband houdt met nabijgelegen waarden — c
betekent dat de juiste noemer “iets meer” is dan de getoonde noemer, en d
betekent dat de juiste noemer “iets minder” is.
Ingevoerde waarde Interne waarde Getoonde breuk
2 3/82,37500000000 +
14 15/32 14,4687500000 +
54/12 4,50000000000 +
6 18/59,60000000000 +
34/12 2,83333333333 + T
15/8192 0,00183105469 + S
12345678 12345/312349793,0000
16 3/16384 16,0001831055 +
0 7/16
6
16
/
0 7/16 0 7/16
(0.40625)
6.5
16
/
7
16
/
7.5
16
/
8
16
/
(0.43750) (0.46875)

5-4 Breuken
Dit is vooral belangrijk als u de regels verandert volgens welke een breuk wordt
weergegeven. (Zie “De weergave van breuken veranderen” verderop.)
Bijvoorbeeld, als u eist dat alle breuken de noemer 5 hebben, dan zal 2/3 worden
getoond als +c omdat de juiste breuk ongeveer 3,3333/5 is, “iets meer” dan
3/5. En, –2/3 is wordt getoond als . +c omdat de echte noemer “iets meer”
is dan 3.
Soms ziet u een annunciator die u niet verwacht. Bijvoorbeeld, als u 2 2/3 invoert,
ziet u +c, hoewel dat precies de juiste waarde is. De rekenmachine vergelijkt
altijd de getoonde breuk met de interne waarde van 12 cijfers. Heeft de interne
waarde een geheel gedeelte, dan is het gedeelte achter de komma korter dan 12
cijfers en het kan onmogelijk overeenkomen met een breuk die alle 12 cijfers
gebruikt.
De weergave van breuken veranderen
In de standaardinstelling toont de rekenmachine een breuk volgens bepaalde
regels. U kunt de regels echter veranderen als u breuken op een andere manier wilt
weergeven:
U kunt een maximum instellen voor de getoonde noemer.
U kunt een van de drie indelingen kiezen.
Hierna bespreken we hoe u de weergave verandert.
Een maximum voor de noemer opgeven
Bij iedere breuk kiest de rekenmachine een noemer die afhangt van de opgeslagen
waarde. Schrijft u een breuk als a b/c, dan is /c de waarde die de noemer
bepaalt.
De waarde van /c bepaalt alleen het maximum van de noemer bepaalt alleen het
maximum van de noemer die bij de weergave wordt gebruikt — de noemer die in
werkelijkheid wordt gebruikt hangt af van de waarde van de breuk (zie hierna).
Breuken 5-5
Om het maximum in te stellen voor de noemer, voer de waarde in en druk
dan z. De Breuk-weergave wordt nu automatisch ingesteld. De waarde
die u invoert kan niet meer zijn dan 4095.
Om de waarde van /c in het X-register op te roepen, drukt u op z.
Om de standaardwaarde van 4095 te herstellen, druk op z of
voer elke waarde groter dan 4095 in als de maximum noemer. Weer wordt
de Breuk-weergave modus automatisch ingesteld.
De functie /c gebruikt de absolute waarde van het gehele getal in het X-register. De
inhoud van LAST X wordt niet veranderd.
Als de weergegeven breuk te lang is om op het scherm te passen, verschijnt de ¨
annunciator; u kunt dan {Ö en {Õ om pagina voor pagina te scrollen
om de rest van de breuk te kunnen zien. Voor het zien van de decimale
representatie van het nummer, druk op z en houdt vast.
Voorbeeld:
Dit voorbeeld toont de vereiste stappen om de maximum noemer op 3125 te zetten
en dan een breuk te laten zien die te lang is voor het scherm.
Voetnoten:
1. In ALG stand, kunt u een expressie invoeren in regel 1 en dan op z
drukken. In dit geval, wordt de expressie geëvalueerd en het resultaat wordt
bepaald om de maximum noemer te bepalen.
Invoer: Weergave: Omschrijving:
z
Stel het maximum van de noemer
in op 3125.
{#
+
Let op de missende cijfers in de
noemer.
Õ
Scroll naar rechts om de rest van
de noemer te kunnen zien.
5-6 Breuken
2. In de ALG stand, kunt u het resultaat van een berekening gebruiken als
argument voor de /c functie. Met de waarde in regel 2, druk eenvoudig
z. De waarde in regel 2 wordt weergegeven in Breuk formaat en het
gehele deel wordt gebruikt om de maximum noemer te bepalen.
3. U kunt niet een complex nummer of een vector gebruiken als argument voor de
/c commando. De foutmelding “# !” wordt dan getoond.
De weergave van een breuk kiezen
De rekenmachine heeft drie breukformaten. De weergegeven breuken zijn altijd de
meest accurate breuken binnen de regels van het geselecteerde formaat.
Nauwkeurigste breuk. Een breuk kan iedere noemer hebben met de
waarde van /c als maximum, en hij wordt zo veel mogelijk vereenvoudigd.
Als u bezig bent met wiskundeconcepten waaraan breuken te pas komen,
dan zult u iedere mogelijkee noemer willen zien. De waarde van /c is dan
4095. Dit is de standaardwaarde.
Factoren van noemer. Breuken kunnen alleen een noemer hebben die
een factor is van waarde van /c, en ze worden zo veel mogelijk
vereenvoudigd. Bijvoorbeeld, als u aandelenkoersen berekent, dan wilt u
waarden zien als + en + (/c is 8). En als /c 12 is, dan zijn
mogelijke noemers 2, 3, 4, 6 en 12.
Vaste noemer. Breuken worden altijd getoond met de waarde van /c als
noemer— zonder te vereenvoudigen. Als u werkt met tijden, dan zult u
waarden willen zien als + (/c is 60).
Er zijn drie flags die de breukwaarde controleren. Deze flags hebben als nummer 7,
8 en 9. Elke flag is of gewist of gezet. Hun doeleinden zijn als volgt:
Flag 7 zet de breuk-weergave modus aan of uit; gewist=off en
ingesteld=on.
Flag 8 schakelt tussen elke waarde gebruiken die minder dan of gelijk is
aan de /c waarde of alleen factoren van de /c waarde gebruikt; clear =
gebruik elke waarde en set = alleen factoren van de /c waarde
gebruiken.
Flag 9 werkt alleen als Flag 8 is gezet en schakelt tussen het reduceren of
niet reduceren van de breuken; clear = reduceren en set = niet reduceren.
Met flags 8 en 9 naar behoren gewist of gezet, kunt u de drie weergaven verkrijgen
als hieronder in de tabel:

Breuken 5-7
U kunt de flags 8 en 9 en daarmee de weergave van een breuk beïnvloeden. (Flags
zijn vooral in programma’s handig en worden daarom gedetailleerd behandeld in
hoofdstuk 14.)
1. Druk op zx om het flagmenu te openen.
2. Om een flag te zetten, drukt u ( ) en geeft u het nummer van de flag op,
bijvoorbeeld 8.
Om een flag te wissen, drukt u op () en toetst u het nummer van de
flag in.
Wilt u de waarde van een flag zien, druk dan op ( @) en toets het
nummer van de flag in. Druk op of a om te reageren op & of .
Voorbeeld:
Dit voorbeeld toont de weergave van breuken in de drie formaten met gebruik van
het getal π. Dit voorbeeld neemt aan dat de breuk-weergave formaat aktief is en dat
Flag 8 in zijn standaardstand staat (gewist).
Om deze weergave te krijgen: Verandert u deze flags:
89
Nauwkeurigste breuk Gewist —
Factoren van noemer Gezet Gewist
Vaste noemer Gezet Gezet
Invoer: Weergave: Omschrijving:
z
Zet de maximum /c waarde terug
naar standaard.
zj
+
Nauwkeurigste formaat
Flag 8= gewist.
zx( )
+
Flag 8= gezet;
Factoren van noemer formaat;
819*5=4095
zx( )
+
+
Flag 9= gezet;
Vaste noemer formaat
zx()
zx(
)
+
Keert terug naar
standaardformaat (nauwkeurigste
breuk)

5-8 Breuken
Voorbeelden van getoonde breuken
De volgende tabel toont hoe het getal 2,77 eruit ziet in de drie manieren van
weergave met twee waarden van /c.
De volgende tabel toont hoe verschillende getallen worden weergegeven als /c een
waarde heeft van 16.
Breuken afronden
Worden breuken als breuken weergegeven, dan converteert de functie RND het
getal in het X-register tot de dichtstbijzijnde decimale weergave van de breuk. Er
wordt afgerond volgens de huidige waarde van /c
en de toestand van de flags 8
en 9. De nauwkeurigheidsannunciator wordt uitgezet als het resultaat precies
overeenkomt met de decimale weergave van de breuk. Anders blijft de
nauwkeurigheidsannunciator aanstaan (Zie “Nauwkeurigheidsannunciators” eerder
in dit hoofdstuk.)
In een vergelijking of programma zal de functie RND afronden op een breuk als
weergave van breuken actief is.
Gewenste
weergave
Hoe 2,77 wordt getoond
/c
= 4095
/c
= 16
Nauwkeurigste breuk 2 77/100 (2,7700) 2 10/13S(2,7692)
Factoren van noemer 2 1051/1365S(2,7699) 2 3/4S(2,7500)
Vaste noemer 2 3153/4095S(2,7699) 2 12/16S(2,7500)
Gewenste
weergave
Ingevoerd getal en weergegeven breuk
22,52
2
/
3
2,9999 2
16
/
25
Nauwkeurigste breuk
2 2 1/2 2 2/3
S
3
T
2 9/14
T
Factoren van noemer
2 2 1/2 2 11/16
T
3
T
2 5/8
S
Vaste noemer
2 0/16 2 8/16 2 11/16
T
3 0/16
T
2 10/16
S
Waarbij /c
de waarde 16 heeft.

Breuken 5-9
Voorbeeld:
Stel dat u een ruimte hebt van 56 3/4 cm die u in zes gelijke stukken wilt verdelen.
Hoe breed is ieder deel, als u kunt meten met een nauwkeurigheid van 1/16 cm?
Hoe groot is de cumulatieve fout?
Breuken in vergelijkingen
U kunt een breuk in een vergelijking gebruiken. Wanneer een vergelijking wordt
weergegeven, worden alle nummerieke waarden in de vergelijking getoond zoals
ze zijn ingevoerd. Ook is de breuk-weergave beschikbaar voor bewerkingen met
betrekking tot vergelijkingen.
Evalueert u een vergelijking en wordt er gevraagd om een waarde, dan kunt u een
breuk invoeren. De waarde wordt getoond volgens de huidige instelling van de
weergave.
Zie hoofdstuk 6 voor informatie over het werken met vergelijkingen.
Invoer: Weergave: Omschrijving:
z x Zet flag 8
z Zorgt voor weergave in stappen
van 1/16 cm. (Flags 8 en 9
moeten hetzelfde zijn als in het
vorige voorbeeld.)
{HD
+ Slaat de afstand op in D.
p +SDe stukken zijn iets breder dan
9 7/16 cm.
{ I + De breedte wordt hierop afgerond.
y + Breedte van de zes stukken.
KD . + De cumulatieve fout.
z x(). + Wist flag 8.
{ .) Zet weergave van breuken uit.

5-10 Breuken
Breuken in programma’s
U kunt een breuk in een programma op dezelfde manier gebruiken als in een
vergelijking; nummerieke waarden worden getoond zoals ze zijn ingevoerd.
Wordt een programma uitgevoerd, dan worden de waarden getoond volgens de
gewenste instelling als het aktief is. Wordt er door een INPUT-instructie om een
waarde gevraagd, dan mag u die invoeren, Het resultaat van het programma wordt
weergegeven met het huidige weergave formaat.
Een programma kan de weergave van breuken veranderen met de functie /c
functie
en door de flags te veranderen 7, 8, en 9. Zie “Flags” in hoofdstuk 14.
Zie hoofdstuk 13 en 14 voor informatie over het werken met programma’s.

Vergelijkingen invoeren en evalueren 6-1
6
Vergelijkingen invoeren en evalueren
Hoe u vergelijkingen kunt gebruiken
U kunt op diverse manieren vergelijkingen gebruiken op de HP 35s:
Om een vergelijking op te geven om te evalueren (dit hoofdstuk).
Om een vergelijking op te geven die moet worden opgelost voor onbekende
waarden (hoofdstuk 7).
Om een functie op te geven die geïntegreerd moet worden (hoofdstuk 8).
Voorbeeld: Rekenen met een vergelijking.
Stel dat u vaak de inhoud moet berekenen van een stukje pijp. De vergelijking is
V = .25
π
d2 l
Hierin is d
de binnendiameter van de pijl, en l
de lengte.
U zou de vergelijking steeds weer opnieuw kunnen invoeren. Bijvoorbeeld,
zMy{:yy waarmee u de
inhoud berekent van een pijp met een lengte van 16 centimeter en een diameter
van 2 1/2 centimeter (78,5398 kubieke centimeter). Door echter een vergelijking
op te slaan, zal de HP 35s de relatie tussen diameter, lengte en inhoud
“onthouden”, zodat u er steeds weer gebruik van kunt maken.
Zet de rekenmachine in de vergelijkingenstand en geef de vergelijking op met de
volgende procedure:
6-2 Vergelijkingen invoeren en evalueren
Door de controlesom en de lengte van de vergelijking te vergelijken met het
voorbeeld, weet u of u de vergelijking correct hebt ingevoerd. (Zie “Vergelijkingen
controleren” aan het einde van dit hoofdstuk voor meer informatie.)
Evalueer de vergelijking (om V
te berekenen):
Invoer: Weergave: Omschrijving:
G ! !
van de huidige
vergelijking in regel 2.
Selecteert de vergelijkingenstand,
wat blijkt uit de annunciator
EQN.
KBegint een nieuwe vergelijking,
K zet de A..Z annunciator
aan zodat u de naam van de
variabele in kunt voeren.
#zc #/_K#typt #
#/)_Bij invoer van cijfers wordt de “_”
invoer cursor gebruikt.
yzMy #/)ºπº_y rondt het getal af.
KD0 #/)ºπº: _0 typt :.
yK #/)ºπº:º_
#/)ºπº:º Bepaalt en geeft de vergelijking
weer.
z /
/
Toont de controlesom en de lengte
van de vergelijking, zodat u de
invoer kunt controleren.
Invoer: Weergave: Omschrijving:
@
waarde
Er wordt gevraagd om variabelen
aan de rechterkant van de
vergelijking. Er wordt eerst om D
gevraagd; de waarde is de huidige
waarde van D.
@
+_
Geef 2 1/2
cm op als een breuk.
f@
waarde
D wordt opgeslagen, er wordt om L
gevraagd, de waarde is de huidige
waarde van L.
f #/
)
L wordt opgeslagen; V wordt
berekend in kubieke centimeters. Het
resultaat wordt in V opgeslagen.

Vergelijkingen invoeren en evalueren 6-3
Samenvatting van bewerkingen in vergelijkingen
Alle vergelijkingen die u maakt worden opgeslagen in de lijst van vergelijkingen.
Deze lijst ziet u als u de vergelijkingenstand activeert.
U gebruikt bepaalde toetsen om bewerkingen met vergelijkingen uit te voeren.
Deze worden verderop besproken.
Wanneer vergelijkingen worden weergegeven in de lijst van vergelijkingen, worden
elke keer twee vergelijkingen weergegeven. De aktieve vergelijking is te zien in
regel 2.
U kunt ook vergelijkingen gebruiken in programma’s. Dit wordt in hoofdstuk 13
behandeld.
Toets Bewerking
GOpent en sluit de vergelijkingenstand.
Evalueert de getoonde vergelijking. Is de vergelijking
een toekenning, dan wordt de rechterzijde
geëvalueerd en het resultaat opgeslagen in de
variabele aan de linkerkant. Is de vergelijking een
gelijkheid
of expressie, dan wordt de waarde
berekend als W. (Zie “Soorten vergelijkingen”
verderop in dit hoofdstuk.)
WEvalueert de getoonde vergelijking. Berekent de
waarde en vervangt “=” door “-” als er een “=” is.
Lost de getoonde vergelijking op voor de door u
opgegeven onbekende variabele. (Zie hoofdstuk 7.)
z )Integreert de getoonde vergelijking naar de door u
opgegeven variabele. (Zie hoofdstuk 8.)
aVerwijdert de huidige vergelijking of verwijdert het
element links van de cursor.
Ö of ÕBegint met het bewerken van de weergegeven
vergelijking, verplaatst alleen de cursor en verwijdert
niets in de inhoud.
{Ö of {ÕScrollt het huidige scherm van de
vergelijkingsweergave.
×of ØBladert op en neer door de lijst van vergelijkingen.
{× of {ØSpringt naar de top of bodem van de lijst van
vergelijkingen.
z Toont de controlesom (ter verificatie) en lengte (aantal
bytes) van de getoonde vergelijking.
z:Herstelt de meest recent verwijderde elementen of
vergelijkingen.
Verlaat de vergelijkingenstand.

6-4 Vergelijkingen invoeren en evalueren
Vergelijkingen aan de lijst van vergelijkingen
toevoegen
De lijst van vergelijkingen
is een verzameling van vergelijkingen die u hebt
ingevoerd. De lijst is opgeslagen in het geheugen van de rekenmachine. Iedere
vergelijking die u opgeeft wordt automatisch aan de lijst toegevoegd.
Een vergelijking invoeren:
U kunt een vergelijking maken zo lang als u wilt- het is alleen beperkt door het
beschikbare geheugen.
1. Zorg ervoor dat de rekenmachine in de normale bedrijfsstand staat, meestal
met een getal op het scherm. U bekijkt dus niet de catalogus van variabelen of
programma’s.
2. Druk op G. De annunciator EQN laat zien dat u nu in de
vergelijkingenstand staat. Een van de vergelijkingen in de lijst staat op het
scherm.
3. Begin een vergelijking te typen. De vergelijking op het scherm wordt nu
vervangen door de vergelijking die u typt — de vorige vergelijking wordt
echter niet beïnvloed. Maakt u een fout, druk dan op a of z: om
te corrigeren.
4. Druk op om de vergelijking te voltooien en deze op het scherm te
zien. De vergelijking wordt automatisch in de lijst opgeslagen — direct na de
vergelijking die u zag voorat u begon met typen. (Drukt u in plaats daarvan op
, dan wordt de vergelijking opgeslagen en de vergelijkingenstand
beëindigd.)
Vergelijkingen kunnen variabelen, getallen,vectoren, functies en haakjes bevatten.
Ze worden hierna besproken. Het volgende voorbeeld illustreert deze elementen.
Variabelen in vergelijkingen
U kunt elk van de variabelen van de rekenmachine in een vergelijking gebruiken: A
tot en met Z, (I) en (J). Iedere variabele kunt u zo vaak gebruiken als u wilt. (Voor
informatie over (I) en (J), zie “Variabelen en Labels indirect adresseren” in
hoofdstuk 14.)
Om een variabele in een vergelijking op te nemen, drukt u op K variabele.
Drukt u op K, dan verschijnt de annunciator A..Z om aan te geven dat u een
naam moet opgeven voor de vergelijking.
Vergelijkingen invoeren en evalueren 6-5
Getallen in vergelijkingen
U kunt elk geldig getal in een vergelijking opnemen, inclusief basis 2, 8 en 16,
echt, complex en breukgetallen. Getallen zijn altijd te zien met de ALL weergave,
welke maximaal 12 tekens toont.
Om een getal in een vergelijking op te nemen, gebruikt u de gewone cijfertoetsen,
inclusief , _, en `. Gebruik _ niet om af te trekken.
Functies in vergelijkingen
U kunt veel van de functies van de HP 35s in een vergelijking gebruiken. Een
volledige lijst staat onder “Vergelijkingfuncties” verderop in dit hoofdstuk. U vindt ze
ook in aanhangsel G, “Index van bewerkingen”.
Toetst u een vergelijking in, dan typt u functies op ongeveer dezelfde manier als
wanneer u ze in gewone algebraïsche vergelijkingen gebruikt:
In een vergelijking staan sommige functies gewoonlijk tussen de argumenten,
bijvoorbeeld “+” en “÷”. Zulke infix-operators typt u in een vergelijking in
dezelfde volgorde.
Andere functies hebben een of meer argumenten na
de naam van de functie,
zoals “COS” en “LN”. Zulke prefix-functies typt u in een vergelijking op de
plek waar de functie voorkomt – er verschijnt dan een linker haakje en
daarna kunt u de argumenten intoetsen.
Als een functie twee of meer argumenten heeft, druk op z om ze te
scheiden.

6-6 Vergelijkingen invoeren en evalueren
Haakjes in vergelijkingen
U kunt haakjes gebruiken om te bepalen in welke volgorde de bewerkingen worden
uitgevoerd. Druk op 4 om haakjes toe te voegen. (Meer informatie vindt u in
“Volgorde van bewerkingen” verderop in dit hoofdstuk.)
Voorbeeld: Een vergelijking invoeren.
Voer de vergelijking in r = 2 × c ×(t – a)+25
Vergelijkingen weergeven en selecteren
De vergelijkingenlijst bevat twee ingebouwde vergelijkingen, 2*2 lin.solve en 3*3
lin.Solve, en de vergelijkingen die u heeft ingevoerd. U kunt de vergelijkingen
weergeven en een kiezen om er mee te werken.
Invoer: Weergave: Omschrijving:
G#/)ºπº:º Toont de laatste vergelijking die in
de lijst staat.
Kzc /_Maakt een nieuwe vergelijking
met de variabele R.
/ _Voer een getal in.
yKy /ºº_Infix-operators.
4/ºº12 Een prefix-functie met een linker
haakje.
K!K
Õ /ºº1!.2- _
Het argument en een rechter
haakje.
/ºº1!.2- Voltooit de vergelijking en geeft
deze weer.
z /
/
Geeft de controlesom en lengte
weer.
Verlaat de vergelijkingenstand.

Vergelijkingen invoeren en evalueren 6-7
Vergelijkingen weergeven:
1. Druk op G. Hiermee start u de vergelijkingenstand en wordt de
annunciator EQN weergegeven. Het scherm toont een van de vergelijkingen
uit de lijst:
! ! als de vergelijkingenwijzer boven aan de lijst staat.
De huidige vergelijking (de laatste vergelijking die u bekeek).
2. Druk op × of Ø om door de vergelijkingenlijst te bladeren en iedere
vergelijking te bekijken. De lijst “cirkelt rond” aan de top en bodem.
! ! markeert de “top” van de lijst.
Een lange vergelijking bekijken:
1. Geef de vergelijking weer in de vergelijkingenlijst, zoals hierboven. Is hij
langer dan 14 tekens, dan worden er maar 14 tekens getoond. De
annunciator ¨ geeft aan dat er rechts nog meer tekens zijn.
2. Druk Õ om te beginnen met het bewerken van de vergelijking vanaf het
begin, of druk Ö om de vergelijking te bewerken aan het eind. Druk dan
herhaaldelijk op Ö of Õ om de cursor te verplaatsen door de vergelijking,
elke keer een teken. § en ¨ worden weergegeven als er meer tekens links of
rechts staan.
3. Druk {Öof {Õ om de lange vergelijkingen in regel 2 te scrollen bij
het scherm.
Een vergelijking selecteren:
Geef de vergelijking weer in de vergelijkingenlijst, zoals hierboven. De
weergegeven vergelijking in regel 2 zal worden gebruikt voor alle bewerkingen.
Voorbeeld: Een vergelijking bekijken.
Verwijder het niet-verplichte rechter haakje uit de vergelijking van het vorige
voorbeeld.
Invoer: Weergave: Omschrijving:
G/ºº1!.2- Geeft de huidige vergelijking weer in
de vergelijkingenlijst.
Õ/ºº1!.2- Aktiveert de cursor links van de
vergelijking
Ö/ºº1!.2-_Aktiveert de cursor rechts van de
vergelijking
Verlaat de vergelijkingenstand.

6-8 Vergelijkingen invoeren en evalueren
Vergelijkingen bewerken en wissen
U kunt een vergelijking tijdens het typen bewerken of wissen. U kunt ook
vergelijkingen bewerken of wissen die zijn opgeslagen in de vergelijkingenlijst.
Maar, u kunt de twee ingebouwde vergelijkingen 2*2 lin. solve en 3*3 lin .solve
niet bewerken of wissen. Als u een vergelijking probeert te plaatsen tussen de twee
ingebouwde vergelijkingen, zal de nieuwe vergelijking worden geplaatst achter
3*3 lin.solve.
Een vergelijking bewerken tijdens het typen:
1. Druk Öof Õ om de cursor tekens te laten plaatsen voor de cursor.
2. Beweeg de cursor en druk op a meerdere malen om het ongewenste getal
of functie te verwijderen. Het indrukken van a wanneer de bewerkingslijn
van de vergelijking leeg is, heeft geen resultaat, maar het indrukken van
op een lege vergelijkingsregel verwijdert de lege vergelijkingsregel.
Het scherm toont dan de vorige invoer in de vergelijkingenlijst.
3. Druk op (of ) om de vergelijking op te slaan in de
vergelijkingenlijst.
Een opgeslagen vergelijking bewerken:
1. Geeft de gewenste vergelijking weer, druk op Õ om de cursor aan het begin
van de vergelijking te laten starten of druk op Ö om de cursor aan het eind
van de vergelijking te laten starten. (Zie “vergelijkingen weergeven en
selecteren “ hierboven).
2. Wanneer de cursor aktief is in de vergelijking, kunt u de vergelijking bewerken
net zoals wanneer u een nieuwe vergelijking invoert.
3. Druk op (of ) om de gewijzigde vergelijking op te slaan in de
vergelijkingenlijst, waarbij de vorige versie vervangen wordt.
Menu’s gebruiken tijdens het bewerken van een vergelijking:
1. Wanneer een vergelijking wordt bewerkt, zal het selecteren van een
instellingsmenu (zoals 9, z8, of {) de
bewerkingsstatus van de vergelijking doen afsluiten.
2. Wanneer een vergelijking wordt bewerkt, zal na de selectie van een plaats of
view menu (Zoals ,, z/, {2, {5, {w,
z>,9, zX en z) de vergelijking nog steeds in
de bewerkingsstand staan na het plaatsen van het object.
3. De menu’s l, x,{n zijn gestart in de vergelijkingsstand.

Vergelijkingen invoeren en evalueren 6-9
Een opgeslagen vergelijking verwijderen:
Scroll de vergelijkingenlijst omhoog of omlaag totdat de gewenste vergelijking in
regel 2 van het scherm staat, en druk dan op a.
Alle opgeslagen vergelijkingen verwijderen:
In de EQN stand, druk op {. Selecteer (). Het @ &
menu wordt weergegeven. Selecteer Ö (Y) .
Voorbeeld: Een vergelijking bewerken.
Verwijder 25 uit de vergelijking in het vorige voorbeeld.
Soorten vergelijkingen
De HP 35s werkt met drie soorten vergelijkingen:
Gelijkheden. De vergelijking bevat een “=” en links daarvan meer dan
een enkele variabele. Bijvoorbeeld, x
2 + y
2 = r
2 is een gelijkheid.
Toekenningen. De vergelijking bevat een “=” en links daarvan een enkele
variabele. Bijvoorbeeld, A = 0,5 x b x h is een toekenning.
Invoer: Weergave: Omschrijving:
G/ºº1!.2- Toont de huidige vergelijking in de
vergelijkingenlijst.
Ö/ºº1!.2-_Start de cursor aan het eind van de
vergelijking
aaa /ºº 1!.2_Verwijdert het getal 25.
/ºº1!.2
Toont het einde van de gewijzigde
vergelijking in de vergelijkingenlijst.
Verlaat de vergelijkingenstand.

6-10 Vergelijkingen invoeren en evalueren
Expressies. De vergelijking bevat geen “=”. Bijvoorbeeld, x3 + 1 is een
expressie.
Rekent u met een vergelijking, dan kunt u ieder type gebruiken — maar het type
kan invloed hebben op de wijze van evaluatie. Lost u een probleem op voor een
onbekende variabele, dan geeft u waarschijnlijk de voorkeur aan een gelijkheid of
een toekenning. Integreert u een functie, dan ligt een expressie voor de hand.
Vergelijkingen evalueren
Een van de handigste eigenschappen van vergelijkingen is dat ze geëvalueerd
kunnen worden — ze kunnen numerieke waarden genereren. Hierdoor kunt u het
resultaat van een vergelijking berekenen. (U kunt vergelijkingen ook oplossen en
integreren, zoals u leest in de hoofdstukken 7 en 8).
Doordat veel vergelijkingen bestaan uit twee zijden, gescheiden door “=”, is de
waarde van een vergelijking het verschil
tussen de waarden aan weerszijden. Bij
een berekening wordt “=” beschouwd als “–”. Het resultaat geeft aan in welke mate
de linker- en rechterzijde van de vergelijking overeenkomen.
De HP 35s heeft twee toetsen om vergelijkingen te evalueren: en W. Ze
verschillen alleen in de behandeling van toekenningen:
W geeft de waarde van de vergelijking, ongeacht het soort vergelijking.
geeft de waarde van de vergelijking — tenzij het een toekenning is.
In dat geval geeft de waarde van de rechterzijde, en bovendien
wordt die waarde “opgeslagen” in de variabele aan de linkerzijde — het
resultaat blijft dus bewaard.
De volgende tabel toont de twee manieren om vergelijkingen te evalueren.
Vergelijkingen invoeren en evalueren 6-11
Een vergelijking evalueren:
1. Toon de gewenste vergelijking. (Zie “Vergelijkingen weergeven en selecteren”
hierboven.)
2. Druk op of W. De vergelijking vraagt om een waarde voor elke
benodigde variabele. (Als de basis van een getal in de vergelijking anders is
dan van de huidige basis, zal de rekenmachine automatisch het resultaat van
de huidige basis veranderen).
3. Geef bij iedere prompt de gewenste waarde op:
Als de weergegeven waarde goed is, druk dan op f.
Wilt u een andere waarde, geef die dan op en druk op f. (Zie ook
“Antwoorden op de prompt van een vergelijking” verderop in dit
hoofdstuk.)
Om een berekening af te breken, druk op of f. Het bericht !"!
wordt getoond in regel 2.
Om een vergelijking te evalueren worden er geen waarden van de stapel gehaald
— er worden alleen getallen in de vergelijking en variabelen gebruikt. De waarde
van de vergelijking komt in het X-register.
ENTER gebruiken voor evaluatie
Staat er een vergelijking in de vergelijkingenlijst, dan kunt u met de
vergelijking evalueren. (Bent u bezig een vergelijking in te voeren, dan beëindigt
het invoeren, zonder de vergelijking te evalueren.)
Soort vergelijking Resultaat van
Resultaat van
W
Gelijkheid: g(x) = f(x)
Voorbeeld: x2 + y2 = r2
g(x) – f(x)
x2 + y2– r2
Toekenning: y = f(x)
Voorbeeld: A = 0,5 × b x h
f(x)
0,5 × b × h
y – f(x)
A – 0,5 × b × h
Expressie: f(x)
Voorbeeld: x3 + 1
f(x)
x3 + 1
Bovendien wordt het resultaat in de variabele links opgeslagen, bijvoorbeeld
in A.
6-12 Vergelijkingen invoeren en evalueren
Als de vergelijking een toekenning is, wordt alleen de rechte zijde
geëavalueerd. Het resultaat komt dan in het X-register en wordt opgeslagen
in de linker variabele, de variabele wordt dan getoond in het scherm.
vindt de waarde in de linker variabele.
Als de vergelijking een gelijkheid of expressie is, wordt de gehele
vergelijking geëvalueerd- precies zoals voor W. Het resultaat komt dan in
het X-register.
Voorbeeld: Een vergelijking evalueren met ENTER.
Gebruik de vergelijking uit het begin van dit hoofdstuk om de inhoud te berekenen
van een pijp met een middellijn van 35-mm en een lengte van 20 meter.
XEQ gebruiken voor evaluatie
Staat er een vergelijking in de vergelijkingenlijst, dan kunt u die evalueren met
W De hele vergelijking wordt geëvalueerd, ongeacht het type van de
vergelijking. Het resultaat komt in het X-register.
Invoer: Weergave: Omschrijving:
G
( × zonodig)
#/)ºπº:º Geeft de gewenste
vergelijking weer.
@
)
Evalueert de toekenning,
zodat de waarde wordt
opgeslagen in V. Vraagt om
variabelen aan de
rechterzijde van de
vergelijking. De huidige
waarde van D
is 2,5.
f @
Slaat D
op en vraagt om L,
waarvan de huidige waarde
16 is.
y
f
#/
88)
Slaat L op in millimeters;
berekent V in kubieke
millimeters, slaat het
resultaat op in V, en toont V.
p`
) Verandert kubieke
millimeters in liters (zonder V
te veranderen).
Vergelijkingen invoeren en evalueren 6-13
Voorbeeld: Een vergelijking evalueren met XEQ.
Gebruik de resultaten van het vorige voorbeeld om vast te stellen hoeveel de inhoud
van de pijp verandert als de diameter wordt veranderd in 35,5 millimeter.
De waarde van de vergelijking is het oude volume (van V) min het nieuwe volume
(berekend met gebruik van de nieuwe D waarde) — zodat het oude volume kleiner
is met de getoonde hoeveelheid.
Antwoorden op de prompt van een vergelijking
Wanneer u een vergelijking evalueert, wordt u gevraagd om een waarde voor elke
benodigde variabele. De prompt geeft de naam van de variabele en zijn huidige
waarde, zoals %@). Als de indirecte variabele zonder naam (I) of (J) in een
vergelijking staat, wordt u niet gevraagd om zijn waarde, aangezien de huidige
opgeslagen waarde in de indirecte variabele zonder naam automatisch wordt
gebruikt. (Zie hoofdstuk 14)
Om het getal onveranderd te laten, druk op f.
Invoer: Weergave: Omschrijving:
G#/)ºRº:º Geeft de gewenste vergelijking
weer.
W#@
88)
Start het evalueren van de
vergelijking om de waarde te
bepalen. Er wordt om alle
variabelen gevraagd.
f@
V verandert niet, er wordt om D
gevraagd.
f
@
8
Slaat nieuwe D op, er wordt om L.
gevraagd.
f.8) L
blijft gelijk, de waarde van de
vergelijking wordt berekend — het
verschil tussen de linker- en de
rechterzijde.
p`
.) Verandert kubieke millimeters in
liters.

6-14 Vergelijkingen invoeren en evalueren
Om het getal te veranderen, type het nieuwe getal in en druk op f. Dit
nieuwe getal overschrijft de oude waarde in het X-register. U kunt een getal
als een breuk invoeren als u wilt. Als u een getal moet berekenen, maak dan
normale berekeningen op het toetsenbord, druk dan f. Bijvoorbeeld, u
kunt 2 5 0f in de RPN stand indrukken, of druk 20 5
f in de ALG stand. Voordat u indrukt, zal de expressie
worden getoond in regel 2 en na het indrukken van , wordt het
resultaat van de expressie getoond in regel 2.
Om de prompt te annuleren drukt u op . De huidige waarde van de
variabele blijft in het X-register en aan de rechterzijde getoond van regel
twee. Drukt u op tijdens het invoeren van een getal, dan wordt het getal
nul. gewist. Druk nogmaals op om de prompt te annuleren.
Cijfers tonen die door de prompt verborgen worden. Druk op z .
In de RPN stand, plaatst elke prompt de variabele waarde in het X-register en stopt
het optillen van de stapel. Als u een getal op de prompt intypt, vervangt het de
waarde in het X-register. Wanneer u op f drukt, is het optillen van de stapel
mogelijk, zodat de waarde op de stapel wordt bewaard.
De syntaxis van vergelijkingen
Vergelijkingen volgen bepaalde conventies die bepalen hoe ze geëvealueerd
worden:
Interactie tussen operators.
Geldige functies in vergelijkingen.
Controle op syntaxisfouten.
Volgorde van bewerkingen
Operators in een vergelijking worden verwerkt in een bepaalde volgorde waardoor
de evaluatie logisch en voorspelbaar is:

Vergelijkingen invoeren en evalueren 6-15
Dus alle bewerkingen tussen haakjes worden uitgevoerd vóór de bewerkingen
buiten haakjes.
Voorbeelden:
Volgorde Bewerking Voorbeeld
1Haakjes 1%-2
2Functies 1%-2
3Macht ( 0 ) %:
4Minteken met één operand
(_).
5 Vermenigvuldigen en delen %º&, ª
6 Optellen en aftrekken -, .
7Gelijkheid /
Vergelijkingen Betekenis
º:/ a × (b3) = c
1º2:/ (a × b)3 = c
a + (b/c) = 12
(a + b) / c = 12
01!-8.2: [%CHG ((t + 12), (a – 6)) ]2

6-16 Vergelijkingen invoeren en evalueren
Functies in vergelijkingen
De volgende tabel geeft de functies die geldig zijn in vergelijkingen. U vindt deze
informatie ook in aanhangsel G, “Index van bewerkingen”.
Bij het invoeren van een prefixfunctie verschijnt voor uw gemak direct een linker
haakje.
De prefix-functie die twee argumenten nodig hebben zijn %CHG, XROOT, IDIV,
RMDR, nCr en nPr. Scheid de twee argumenten met een dubbele punt.
In een vergelijking staan de argumenten van XROOT in de omgekeerde volgorde,
vergeleken met RPN. Bijvoorbeeld, –83 . is gelijk aan %!18.
2.
Bij alle andere functies met twee argumenten komen de argumenten in de volgorde
Y, X net als met RPN. Bijvoorbeeld, 28 4 z x is gelijk aan
QT182.
Wees voorzichtig als het tweede argument van een functie negatief is. Dit zijn
geldige vergelijkingen:
LN LOG EXP ALOG SQ SQRT
INV IP FP RND ABS !
SGN INTG IDIV RMDR
SIN COS TAN ASIN ACOS ATAN
SINH COSH TANH ASINH ACOSH ATANH
DEG RAD HMSHMS %CHG XROOT
LGAL MILE KM nCr nPr
KG LB °C °F CM IN
SEED ARG RAND π
+–×÷
^
sx sy
σ
x
σ
y
wrmb
nΣxΣyΣx2Σy2Σxy
xy
xx
ˆy
ˆ

Vergelijkingen invoeren en evalueren 6-17
01.%8.2
01%81.&22
Acht van de vergelijkingen hebben namen die anders zijn dan die van hun
overeenstemmende bewerkingen:
Voorbeeld: Omtrek van een trapezium.
De volgende vergelijking berekent de omtrek van een trapezium. In een boek ziet
de vergelijking er wellicht zo uit:
Omtrek = a + b + h ()
De volgende vergelijking voldoet aan de syntaxis van de HP 35s:
RPN Bewerking Benaming in vergelijking
x2SQ
SQRT
exEXP
10xALOG
1/x INV
XROOT
yx^
INT÷ IDIV
x
Xy
φθ
sin
1
sin
1+
b
a
h
φ
θ

6-18 Vergelijkingen invoeren en evalueren
De volgende vergelijking voldoet ook aan de syntaxis. Deze vergelijking gebruikt
de inverse functie, #1 1!22, in plaats van de breuk ª 1!2. U ziet dat
de functie SIN “genest” is in de functie INV. (INV typt u met 3.)
/--º1#1 1!22-#1 1222
Voorbeeld: Oppervlakte van een veelhoek.
De vergelijking voor de oppervlakte van een regelmatige veelhoek met n
zijden van
lengte d
is:
Oppervlakte =
Deze vergelijking kunt u als volgt opgeve
/)ºº:º 1πª2ª 1πª2
U ziet hoe de operators en functies gecombineerd worden om tot de gewenste
vergelijking te komen.
Haakje gebruikt om objecten te groeperen
Naam van
één letter
Optionele expliciete
vermenigvuldiging
Deling vóór optelling
/n)sin(
)/cos(
4
1
π
πn
n d 2
d
2/n
π

Vergelijkingen invoeren en evalueren 6-19
U kunt de vergelijking met de volgende invoer in de vergelijkingenlijst opnemen:
GKzcyKyK0y
QzMpKÕpNzMpK
Syntaxisfouten
De rekenmachine controleert niet de syntaxis van een vergelijking totdat u de
vergelijking evalueert. Als een fout is ontdekt, wordt &!%
weergegeven en de cursor is dan te zien op de eerste foute plek. U moet de
vergelijking bewerken om de fout te kunnen verbeteren. (Zie “Vergelijkingen
bewerken en wissen” eerder in dit hoofdstuk)
Doordat de HP 35s de syntaxis niet controleert, kunt u “vergelijkingen” maken die in
werkelijkheid berichten zijn. Dit is vooral handig in programma’s, zoals beschreven
is in hoofdstuk 13.
Vergelijkingen controleren
Bekijkt u een vergelijking — dus niet als u een vergelijking invoert — dan kunt u op
z drukken om twee dingen over de vergelijking te tonen: de controlesom
en de lengte van de vergelijking de controlesom en de lengte van de vergelijking.
De waarden blijven op het scherm zolang u ingedrukt houdt.
De controlesom is een hexadecimale waarde die de vergelijking uniek identificeert.
Maakt u een fout in een vergelijking, dan klopt de controlesom niet. De lengte is het
aantal bytes geheugen dat de vergelijking nodig heeft.
Met de controlesom en de lengte kunt u controleren of u een vergelijking goed hebt
ingevoerd. De waarden die op het scherm verschijnen moeten overeenkomen met
de waarden die u in de handleiding ziet.
Voorbeeld: Controlesom en lengte van een vergelijking.
Bepaal de controlesom en de lengte van de vergelijking waarmee de inhoud van
een pijp wordt berekend.

Vergelijkingen oplossen 7-1
7
Vergelijkingen oplossen
In hoofdstuk 6 zagen we hoe u kunt gebruiken om de waarde te vinden
van de variabele aan de linkerzijde van een toekenning. U kunt SOLVE gebruiken
om de waarde te vinden van iedere
variabele in ieder
type vergelijking.
Neem bijvoorbeeld de vergelijking:
x2 – 3y = 10
Kent u de waarde van y
in deze vergelijking, dan kunt u met SOLVE de onbekende
x
vinden. Weet u de waarde van x, dan zoekt SOLVE de onbekende y. Dit werkt
ook met “woordproblemen”:
Aantal x Stuksprijs = Prijs
Kent u twee van de drie variabelen, dan berekent SOLVE de derde.
Is er maar één variabele, of zijn alle variabelen bekend op één na, dan is het
oplossen van x hetzelfde als het vinden van de wortel van de vergelijking. Er is
sprake van een wortel als een gelijkheid of toekenning links en rechts precies
dezelfde waarde oplevert, of als een expressie precies nul is.
Een vergelijking oplossen
Een vergelijking (ingebouwde vergelijkingen niet inbegrepen) voor een onbekende
variabele oplossen:
1. Druk op G en toon de gewenste vergelijking. Typ zo nodig de vergelijking
zoals is uitgelegd in hoofdstuk 6 onder “Vergelijkingen in de vergelijkingenlijst
invoeren.”
7-2 Vergelijkingen oplossen
2. Druk op { en daarna op de toets voor de onbekende variabele.
Druk bijvoorbeeld op { om x
op te lossen. De vergelijking vraagt
dan om een waarde voor alle andere variabelen in de vergelijking.
3. Geef bij iedere prompt de gewenste waarde op:
Als de weergegeven waarde de waarde is die u wilt, druk dan op f.
Wilt u een andere waarde, typ of bereken die dan en druk op f.
(Details vindt u in “Antwoorden op een vergelijkingprompt” in hoofdstuk
6.)
U kunt een lopende berekening afbreken met of f.
Wanneer de wortel is gevonden, wordt het opgeslagen in de relatie–variabele, en
de waarde van de variabele is zichtbaar op het scherm. Hieraan toegevoegd,
bevat het X–register de wortel, het Y–register bevat de vorige geschatte waarde of
Nul, en het Z–register bevat de waarde van de wortel D–waarde (welke nul moet
zijn).
Bij sommige gecompliceerde wiskundige voorwaarden lukt het niet een oplossing te
vinden. De rekenmachine toont dan ! ". Zie “Het resultaat
controleren” later in dit hoofdstuk, en “Resultaten interpreteren” en “Als SOLVE geen
wortel kan vinden” in aanhangsel D.
Bij sommige vergelijkingen kan het gunstig zijn een of twee beginwaarden
in te
toetsen voor de onbekende variabele, voordat u met oplossen begint. Dit kan de
berekening versnellen, het antwoord in de richting van de oplossing leiden, en meer
dan een oplossing opleveren. Zie “Een beginwaarde opgeven” later in dit
hoofdstuk.
Voorbeeld: De vergelijking van een lineaire beweging oplossen.
De vergelijking van de beweging van een vrijvallend voorwerp is:
d = v0 t + 1/2 g t 2
waarin d
de afstand is, v0 de beginsnelheid, t de tijd, en g
de
zwaartekrachtversnelling.
Typ de vergelijking in:

Vergelijkingen oplossen 7-3
g
(zwaartekrachtversnelling) is als variabele opgegeven, zodat u de waarde kunt
veranderen (op de aarde 9,8 m/s2 of 32,2 ft/s2).
Bereken hoeveel meter een voorwerp valt in 5 seconden, als het in rust wordt
losgelaten. De vergelijkingenstand staat nog aan en de gewenste vergelijking staat
al op het scherm, dus u kunt meteen oplossen voor D:
Probeer nu een andere berekening met dezelfde vergelijking: hoe lang duurt het
voor een voorwerp 500 meter gevallen is?
Invoer: Weergave: Omschrijving:
{()
Ö(&)
Maakt geheugen leeg.
G> OLQ) UµO¶H
! !
Selecteert de
vergelijkingenstand.
KzcK
# y K! /#º!-_
Start de vergelijking.
y KGy
K!0
§/#º!-)ºº!: _
/#º!-)ºº!: Besluit de vergelijking en
toont het linkerdeel.
z /
/
Controlesom en lengte.
Invoer: Weergave: Omschrijving:
{ #_ Vraagt om een onbekende
variabele.
#@
waarde
waardeSelecteert D; vraagt
om V.
f !@
waarde
Slaat 0 op in V; vraagt om
T.
f @
waarde
Slaat 5 op in T; vraagt om
G.
f #
/
)
Slaat 9,8 op in G; lost D
op.
7-4 Vergelijkingen oplossen
Voorbeeld: De vergelijking van een ideaal gas oplossen.
De wet van Boyle – Gay Lussac beschrijft de relatie tussen druk, inhoud,
temperatuur en de hoeveelheid (in mol) van een ideaal gas:
P × V = N × R × T
waarin P de druk is (in atmosferen of N/m2), V is het volume (in liters), N is de
hoeveelheid gas in mol, R is de universele gasconstante (0,0821 liter–atm/mol–K of
8,314 J/mol–K), en T is de temperatuur (Kelvin: K=°C + 273,1).
Voert de vergelijking in:
Invoer: Weergave: Omschrijving:
G/#º!-)ºº!: Geeft de vergelijking
weer.
{! @
)
Lost op voor T; vraagt om
D.
f #@
Slaat 500 op in D;
vraagt om V.
f@
)
Bewaart 0 in V; vraagt
om G.
f #
!/
)
Bewaart 9,8 in G; lost T
op.
Invoer: Weergave: Omschrijving:
GKPyº_ Selecteert de
Vergelijkingenstand en
start de vergelijking.
K#zc
Ky
KyK! º#/ºº!_
º#/ºº! Bepaalt en geeft de
vergelijking weer.
z /
/
Controlesom en lengte.
Vergelijkingen oplossen 7-5
Een vat van 2 liter bevat 0,005 mol kooldioxide bij 24°C. We nemen aan dat dit
gas zich als een ideaal gas gedraagt en willen de druk berekenen. De
vergelijkingenstand staat nog aan en de gewenste vergelijking staat al op het
scherm, dus we kunnen meteen P
oplossen:
Een vat van 5 liter bevat stikstof. De druk is 0,05 atmosfeer en de temperatuur is
18°C. Bereken de dichtheid van het gas (N x 28/V, waarin 28 de moleculaire
massa is van stikstof).
Invoer: Weergave: Omschrijving:
{P#@
waarde
Lost P op; vraagt om V.
f @
waarde
Slaat 2 op in V; vraagt om
N.
f @
waarde
Slaat 0,005 op in N;
vraagt om R.
f !@
waarde
Slaat 0,0821 op in R;
vraagt om T.
!@
)
Berekent T (Kelvin).
f #O
/
)
Slaat 297,1 op in T;
berekent P in atmosfeer.
Invoer: Weergave: Omschrijving:
Gº#/ºº! Geeft de vergelijking weer.
{ @
)
Lost N op; vraagt om P.
f #@
)
Slaat 0,05 op in P; vraagt
om V.
f @
)
Slaat 5 op in V; vraagt om
R.
f!@
)
Bewaart de vorige R;
vraagt om T.
!@
)
Berekent T (Kelvin).

7-6 Vergelijkingen oplossen
Ingebouwde Vergelijking oplossen
De ingebouwde vergelijkingen zijn : “2*2 lin. solve” (Ax+By=C, Dx+Ey=F) en
“3*3 lin. Solve”(Ax+By+Cz=D, Ex+Fy+Gz=H, Ix+Jy+Kz=L). Als u een van deze
selecteert, hebben de W, en ) toets geen effekt. Het indrukken
van{ vraagt om 6 variabelen (A tot F) voor 2*2 of 12 variabelen (A tot
L) voor 3*3, en gebruik ze voor vinden het van x, voor een 2*2 liniair
vergelijkingssysteem of x, y en z voor een 3*3 liniair vergegelijkingssysteem. Het
resultaat wordt opgeslagen in de variabelen x, y en z. De rekenmachine kan cases
ontdekken met oneindig veel oplossingen of geen oplossingen.
Voorbeeld: los de x, y op in gelijktijdige vergelijkingen
f #
/
)
Slaat 291,1 op in T; lost N
op.
y ) Berekent de massa in
grammen, N x 28.
K#p ) Berekent de dichtheid in
grammen per liter.
Invoer: Weergave: Omschrijving:
G> OLQ) UµO¶H
! !
Gaat naar de
vergelijkingenstand.
Ø ! !
> OLQ) UµO¶H
Geeft de ingebouwde
vergelijking weer
{ @
waarde
Vraagt om A.
f @
waarde
Slaat 1 op in A; vraagt om
B.
f @
waarde
Slaat 2 op in B; vraagt om
C.
f @
waarde
Slaat 5 op in C; vraagt om
D.
f @
waarde
Slaat 3 op in D; vraagt om
E.
x+2y=5
3x+4y=11

Vergelijkingen oplossen 7-7
Uitleg van SOLVE
SOLVE probeert eerst de vergelijking direct voor de onbekende op te lossen. Lukt
dat niet, dan gaat SOLVE aan het werk met een iteratieve (herhaalde) procedure.
De procedure begint met het evalueren van de vergelijking voor twee
beginwaarden van de onbekende variabele. Gebaseerd op het resultaat hiervan,
genereert SOLVE een andere, betere waarde. Na meerdere iteraties vindt SOLVE
een waarde voor de onbekende waarbij de waarde van de vergelijking nul is.
Evalueert SOLVE een vergelijking, dan gaat dat op dezelfde manier als met W
— een “=“ in de vergelijking wordt beschouwd als een “–” Bijvoorbeeld, de
vergelijking van Boyle – Gay Lussac wordt geëvalueerd als P x V – (N x R x T). Dit
zorgt ervoor dat een gelijkheid of toekenning
bij de wortel in evenwicht is, en dat
een expressie
bij de wortel nul is.
Sommige vergelijkingen zijn moeilijker op te lossen dan andere. Soms moet u
beginwaarden opgeven om een oplossing te kunnen vinden. (Zie “Beginwaarden
kiezen voor SOLVE” hieronder.) Kan SOLVE geen oplossing vinden, dan toont de
rekenmachine ! .
Zie aanhangsel D voor meer informatie over de werking van SOLVE.
Het resultaat controleren
Is de berekening van SOLVE voltooid, dan kunt u controleren of het resultaat
inderdaad een oplossing is van de vergelijking door de waarden in de stapel te
bekijken:
Het X–register (druk op om de VIEW–variabele te verwijderen) bevat de
oplossing (wortel) voor de onbekende; dat wil zeggen, de waarde waarbij
de vergelijking precies nul is.
f @
value
Slaat 4 op in E; vraagt om
F.
f %/ ©
) ª
Slaat 11 op in F en
berekent x en y.
ظ/ ©
) ª
Waarde van y
7-8 Vergelijkingen oplossen
Het Y–register (druk 9) bevat de vorige schatting voor de wortel of is bijna
nul. Dit getal moet hetzelfde zijn als de waarde in het X–register. Als dit niet
het geval is, is de teruggekomen wortel alleen een benadering en de
waarden in de X– en Y– registers zetten de wortel tussen haakjes. Deze
getallen tussen haakjes moeten dicht bij elkaar staan.
Het Z–register (druk weer op 9) bevat de D–waarde van de vergelijking bij
de wortel. Is de wortel precies goed, dan moet hier nul staan. Staat hier niet
nul, dan is de wortel maar een benadering. De waarde moet bijna nul zijn.
Eindigt een berekening met de melding ! , dan kon de rekenmachine
niet naar een wortel convergeren. (U ziet de waarde in het X–register — de laatste
schatting — door de melding te verwijderen met of a.) In het X– en Y–
register vindt u de laatste twee waarden die werden gebruikt bij het zoeken naar de
wortel. In het Z–register vindt u de waarde van de vergelijking bij de laatste
schatting.
Als het X– en Y–register niet dicht bij elkaar staan, of de waarde van het Z–
register niet bijna nul is, is de schatting van het X–register waarschijnlijk niet
nul.
Als de X– en Y– register waarden dicht bij elkaar staan, en de waarde van
het Z–register bijna nul is, is de schatting van het X–register waarschijnlijk
een benadering tot een wortel.
Een SOLVE–berekening onderbreken
Om een berekening af te breken, druk of f en het bericht
“!"!” wordt getoond. De huidige beste schatting van de wortel is de
onbekende variabele; gebruik z om het te bekijken zonder de stapel te
storen, maar er kan niet met oplossen worden doorgegaan.
Beginwaarden opgeven voor SOLVE
De twee beginwaarden komen van:
Het getal dat aanvankelijk in de onbekende variabele is opgeslagen.
Het getal in het X–register (dus op het scherm).
Vergelijkingen oplossen 7-9
Deze getallen worden gebruikt om mee te beginnen, ongeacht of u waarden hebt
opgegeven of niet. Geeft u één beginwaarde op in de variabele, dan is de andere
beginwaarde dezelfde, want die waarde staat nu ook op het scherm. (In dat geval
verandert de rekenmachine één van de getallen een beetje, zodat er toch twee
verschillende beginwaarden zijn.)
Het heeft enkele voordelen om zelf beginwaarden op te geven:
Door het zoekbereik te vernauwen kost het minder tijd om een oplossing te
vinden.
Als er meer dan een exacte oplossing is, kunnen beginwaarden de SOLVE
procedure naar het gewenste antwoord toeleiden of bereik van antwoorden.
Bijvoorbeeld, de vergelijking van een liniaire beweging
d = v0 t + 1/2 gt 2
die twee oplossingen heeft voor t. Het antwoord op de gewenste oplossing
kunt u sturen door de juiste schattingen op te geven.
Het voorbeeld met deze vergelijking, eerder in dit hoofdstuk, had geen
beginwaarden nodig voor het oplossen van T, doordat u in het eerste deel
van het voorbeeld een waarde voor T had opgegeven om D op te lossen. De
waarde in T was goede (realistische) waarde en dus een goede
beginwaarde, toen u T ging oplossen.
Zijn bepaalde waarden voor de onbekende niet toelaatbaar, dan kunt u met
beginwaarden verhinderen dat deze waarden verschijnen. Bijvoorbeeld,
y = t + log x
Resulteert in een fout als x ≤ 0 (melding ! ).
In het volgende voorbeeld heeft de vergelijking meer dan een wortel, maar met
beginwaarden zorgt u ervoor dat de juiste wortel wordt gevonden.

7-12 Vergelijkingen oplossen
De afmetingen van de gewenste doos zijn 50 x 10 x 15 cm. Zou u de maximale
waarde voor de hoogte (20cm) negeren en beginwaarden van 30 en 40 cm
opgeven, dan zou u een hoogte van 42,0256 cm krijgen, wat geen bruikbare
oplossing is. Kiest u kleine beginwaarden, bijvoorbeeld 0 en 10 cm, dan krijgt u
een hoogte van 2,9774 cm — een ongewenste lage doos.
Als u niet weet wat voor waarden u moet gebruiken, kunt u een grafiek gebruiken
om het gedrag van de vergelijking te leren begrijpen. Evalueer uw vergelijking van
diverse onbekende waarden. Voor elk punt in de grafiek, geef de vergelijking weer
en druk W– op de prompt voor x voer de x–coördinaat in, en u krijgt het de
overeenstemmende waarde van de vergelijking, de y–coördinaat. Voor
bovenstaand probleem, moet u altijd V=7500 instellen en de waarde van H
veranderen voor het maken van verschillende waarden voor de vergelijking.
Onthoud dat de waarde voor deze vergelijking het verschil is tussen de linker en
rechterzijde van de vergelijking. De grafische voorstelling van de waarde van deze
vergelijking lijkt hierop.
Meer informatie
Dit hoofdstuk bevat instructies voor het oplossen van onbekende wortels met een
groot aantal toepassingen. Aanhangsel D bevat meer gedetailleerde informatie
over het algoritme van SOLVE, hoe u resultaten interpreteert, wat er gebeurt als er
geen oplossing wordt gevonden, en onder welke voorwaarden u onjuiste resultaten
kunt krijgen.
7500 _ (40_) (20_) 4HHH
20,000
_10,000
50
H
_10

Vergelijkingen integreren 8-3
Voorbeeld: Bessel–functie.
De Bessel–functie van de eerste soort van orde 0 kan worden uitgedrukt als
Bepaal de Bessel–functie voor x = 2 en x = 3.
Voer de expressie in die de functie van de integrand beschrijft:
cos (x sin t )
Integreer deze functie nu naar t tussen nul en π ; m waarbij x = 2.
Invoer: Weergave: Omschrijving:
{
()Ö(&)
Maakt geheugen leeg.
G> OLQ) UµO¶H
! !
Selecteert de
vergelijkingenstand.
QKX 1%2 Geeft de vergelijking op.
yN 1%º 12
K! 1%º 1!22
ÕÕ 1%º 1!22_
1%º 1!22 Besluit de expressie en toont het
begin ervan.
z /
/
Controlesom en lengte.
Verlaat de vergelijkingenstand.
Invoer: Weergave: Omschrijving:
9 ()Selecteert radialen.
z M) Geeft de grenzen van de
integratie (eerst de ondergrens).
G 1%º 1!22 Geeft de functie weer.
z) ∫ G_Vraagt om de variabele
waarnaar geïntegreerd moet
worden.
∫
=
π
π
dttxxJ 0
0)sincos(
1
)(

8-4 Vergelijkingen integreren
Bereken nu J0(3) met dezelfde grenzen van integratie. U moet de grenzen van de
integratie opnieuw bepalen (0, π) aangezien ze van de stapel waren geduwd door
de erop volgende deling van π.
Voorbeeld: Sinusintegraal.
Sommige problemen in de communicatietheorie (bijvoorbeeld pulstransmissie door
geïdealiseerde netwerken) vereisen het berekenen van een integraal (soms
sinusintegraal genoemd) van de vorm
Bepaal Si (2).
!%@
waarde
Vraagt de waarde van X.
f !!
∫ /
)
x = 2. Start de integratie;
berekent het resultaat van
z M p) Het eindresultaat voor J0 (2).
Invoer: Weergave: Omschrijving:
zM ) Geeft de grenzen van de
integratie (eerst de ondergrens).
G 1%º 1!22 Geeft de huidige vergelijking
weer.
z) ∫ G_ Vraagt om de variabele
waarnaar geïntegreerd moet
worden.
!%@
)
Vraagt de waarde van X.
f !!
∫ /
.)
x = 3. Start de integratie;
berekent het resultaat van
.
z M p.) Het eindresultaat voor J0 (3).
∫
π
0 )(tf
∫
π
0 )(tf
dx
x
x
tS t
i)
sin
( )(
0
∫
=

Vergelijkingen integreren 8-5
Voer de expressie in die de functie van de integrand beschrijft:
Als de rekenmachine deze functie op x = 0 probeerde te evalueren, de ondergrens
van de integratie, is een foutmelding (# & ) het resultaat. Maar, normaal
gesproken evalueert de de algoritmische integratie niet op elke grens van de
integratie, tenzij de eindpunten van de interval van de intergratie erg dicht bij
elkaar zijn of het getal of de steekproefpunten zijn extreem groot.
Integreer deze functie nu naar x (dat is X) van nul tot 2 (t = 2).
Invoer: Weergave: Omschrijving:
G> OLQ) UµO¶H
! !
Selecteert de vergelijkingenstand.
NKX 1%2 Start de vergelijking.
Õ 1%2_Het afsluitende haakje is hier niet
nodig.
pKX 1%2ª%_
1%2ª%Besluit de vergelijking.
z /
/
Controlesom en lengte.
Verlaat de vergelijkingenstand.
Invoer: Weergave: Omschrijving:
9 ()Selecteert radialen.
HX
_Geeft de integratiegrenzen op
(eerst de ondergrens).
G 1%2ª%Geeft de huidige vergelijking
weer.
z )X!!
∫ /
)
Berekent het resultaat voor Si(2).
x
xsin

8-6 Vergelijkingen integreren
Nauwkeurigheid van integratie
De rekenmachine kan de waarde van een integraal niet precies berekenen. Het
resultaat is slechts een benadering. De nauwkeurigheid hiervan is afhankelijk van
de nauwkeurigheid van de functie zelf, zoals bekend wordt met uw vergelijking. Dit
wordt beïnvloed door afrondingsfouten door afrondingsfouten in de rekenmachine
en de nauwkeurigheid van empirische constanten.
Integralen van functies met bepaalde karakteristieken zoals steile pieken en snelle
oscillaties kunnen
fout worden berekend, maar waarschijnlijk is dat niet. De
algemene karakteristieken van functies die problemen geven, en de technieken om
ze te vermijden, vindt u in aanhangsel E.
Nauwkeurigheid opgeven
De formaatsinstelling van het scherm (FIX, SCI, ENG, of ALL) bepaalt de
nauwkeurigheid van de integratie berekening; hoe groter het aantal weergegeven
cijfers, des te groter is de nauwkeurigheid van de berekende integraal ( en des te
groter de benodigde tijd om het te berekenen). Als er niet veel cijfers zijn om weer
ter geven, is de berekening des te sneller, maar de rekenmachine neemt dan aan
dat de functie nauwkeurig is aan alleen het aantal opgegeven cijfers.
Om de nauwkeurigheid
van de integratie op te geven, stelt u de weergave zo in dat
het scherm niet meer cijfers toont dan u nauwkeurig genoeg vindt in de waarde van
de integrand. U treft daarna dezelfde nauwkeurigheid aan in het resultaat van de
integratie.
Is het weergeven van breuken ingeschakeld (flag 7 is dan gezet), dan wordt de
nauwkeurigheid bepaald door de vorige instelling van de weergave.
De nauwkeurigheid interpreteren
Na het berekenen van de integraal, zet de rekenmachine de geschatte
onnauwkeurigheid van het resultaat in het Y–register. Druk op Z om de
waarde van de onnauwkeurigheid te zien.
Bijvoorbeeld, is de integraal Si(2)
gelijk aan 1,6054 ± 0,0002, dan is 0,0002 de
fout of onnauwkeurigheid.
Vergelijkingen integreren 8-7
Voorbeeld: Onnauwkeurigheid opgeven.
Staat de weergave ingesteld op SCI 2, bereken dan de integraal in de expressie
van Si(2)
(uit het vorige voorbeeld).
De integraal is 1,61±0,0161. De onnauwkeurigheid heeft geen invloed op de
benadering tot in de derde decimaal, dus u kunt aannemen dat alle weergegeven
cijfers nauwkeurig zijn.
Als de onnauwkeurigheid van een benadering groter is dan wat u wilt toleren, kunt
u het aantal cijfers in het weergave formaat vermeerderen en de integratie herhalen
(aangenomen dat f(x) nog steeds nauwkeurig is berekend tot het aantal cijfers op
het scherm). Over het algemeen, vermindert de onnauwkeurigheid van een
integratie berekening met een tien factor voor elke toegevoegd cijfer, opgegeven in
het schermformaat.
Voorbeeld: De nauwkeurigheid veranderen.
Geef, voor de zojuist berekende integraal van Si(2), op dat het resultaat in vier
decimalen nauwkeurig moet zijn in plaats van twee.
Invoer: Weergave: Omschrijving:
z8
( )
)Geeft wetenschappelijke notatie
op met twee decimalen, zodat de
functie op twee decimalen
nauwkeurig is.
99 )
)
Zet de integratiegrenzen terug van
het Z–en T–register naar het X–en
Y–register.
G 1%2,%Geeft de huidige vergelijking
weer.
z) X !!
∫ /
)
De integraal benaderd op twee
decimalen.
Z). De onnauwkeurigheid van de
benadering van de integraal.

8-8 Vergelijkingen integreren
Deze onnauwkeurigheid geeft aan dat het resultaat misschien tot slechts drie
decimalen nauwkeurig is. In werkelijkheid is het resultaat tot zeven decimalen
nauwkeurig als het wordt vergeleken met de werkelijke waarde van de integraal.
Doordat de onnauwkeurigheid voorzichtig wordt berekend, is de benadering van
de rekenmachine meestal veel gunstiger dan wordt aangegeven.
Meer informatie
Dit hoofdstuk geeft u instructies voor het uitvoeren van integraties met de HP 35s.
Diverse toepassingen werden genoemd. Aanhangsel E bevat meer details over de
werking van het algoritme, voorwaarden die onjuiste resultaten zouden kunnen
opleveren, voorwaarden die de rekentijd verlengen, en het bepalen van de huidige
benadering van een integraal.
Invoer: Weergave: Omschrijving:
z8
( )
). Zet de nauwkeurigheid op vier
decimalen. De fout uit het vorige
voorbeeld staat nog op het
scherm.
99 )
)
Zet de integratiegrenzen terug uit
het Z– en T–register naar het X–
en Y–register.
G 1%2ª%Geeft de huidige vergelijking
weer.
z) X !!
∫ /
)
Berekent het resultaat.
Z). De fout is nu nog maar 1/100
van de fout bij een instelling van
SCI 2.
8 ( )) Herstelt FIX 4 formaat.
9 ()) Herstelt de Graden.

Bewerkingen met complexe getallen 9-1
9
Bewerkingen met complexe getallen
De HP 35s kan werken met complexe getallen van de vorm
º¸ º-¸ T
Er zijn bewerkingen voor complexe berekeningen (+, –, x, ÷), complexe
trigonometrie (sin, cos, tan) en de wiskundige functies –z, 1/z, , ln z, en ez.
(waarin z1
en z2
complexe getallen zijn).
De vorm, x+yi, is alleen beschikbaar in de ALG stand.
Een complex getal invoeren:
Vorm: º¸
1. Typ het reële deel in.
2. Druk op6.
3. Typ het imaginaire deel in.
Vorm: º-¸
1. Typ het reële deel in.
2. Druk op
3. Typ het imaginaire deel in.
4. Druk op6.
Vorm: T
1. Typ de waarde van r in.
2. Druk op{?.
3. Typ de waarde van
θ
in.
De voorbeelden in dit hoofstuk gebruiken allemaal RPN tenzij anders aangegeven.
2
1z
z

9-2 Bewerkingen met complexe getallen
De complexe stapel
Een complex getal neemt deel 1 en deel 2 van een stapel niveau in bezit. In de
RPN stand, wordt het complexe getal dat deel 1 en 2 van het X–register in bezet
neemt weergegeven in regel 2, terwijl het complexe getal dat deel 1 en deel 2 van
het Y–register bezit weergegeven in regel 1.
Complexe bewerkingen
Gebruik de complexe bewerkingen zoals u echte bewerkingen uitvoert in ALG en
RPN stand.
Een bewerking maken met een complex getal:
1. Voer het complexe getal z in zoals hierboven beschreven.
2. Selecteer de complexe functie.
T
Deel 3
Deel 2
Deel 1
Z
Deel 3
Deel 2
Deel 1
Y
Deel 3 (Weergegeven in
regel 1)
X1iY1
Y1 of a1 of
X1 of r1 r1
θ
a1
X
Deel 3
(Weergegeven in
regel 2)
X2iY2
Y2 of a2 of
X2 of r2 r2
θ
a2
Complexe Stapel Complex
resultaat, Z

Bewerkingen met complexe getallen 9-3
Functies voor één complex getal, z
Een berekening maken met twee complexe getallen:
1. Voer het eerste complexe getal z1 in zoals eerder beschreven.
2. Voer het tweede complexe getal z2 zoals eerder beschreven.
3. Kies de rekenkundige bewerking:
Rekenen met twee complexe getallen, z
1
en z
2
Om te berekenen: Drukt u op:
Teken veranderen, –z _
Inverse, 1/z 3
Natuurlijke log, ln z {-
Natuurlijke anti log, ez{*
Sin z N
Cos z Q
Tan z T
Absolute waarde, ABS (z) {A
Argument waarde, ARG (z) z=
Om te berekenen: Drukt u op:
Optelling, z1 + z2
Aftrekking, z1 – z2
Vermenigvuldiging, z1 × z2y
Deling, z1
÷ z2p
Machtsverheffen, 0
2
1z
z

Bewerkingen met complexe getallen 9-5
Evalueer , waarin z = (1i 1).
Complexe getallen in polaire notatie
Veel toepassingen gebruiken reële getallen in polaire vorm of polaire notatie. Ze
gebruiken een paar getallen, net als complexe getallen, en u kunt ermee rekenen
met behulp van de complexe functies.
Voorbeeld: Vectoroptelling.
Tel de volgende drie vectoren op.
6_ ) .)
. +
Invoer van 3i–2/3
y) .) Resultaat is 11,7333i–
3,8667
Invoer: Weergave: Omschrijving:
6 ) )
) )
ENTER 1i1 Gemiddeld
resultaat van
_0 ) .) Z–2, resultaat is 0i–5
{* ) .) Eindresultaten is
0,8776 i – 0,4794.
2−
z
e
r
real
(a, b)
imaginary
θ
imaginair
reële
9-6 Bewerkingen met complexe getallen
U kunt een complexe bewerking met getallen maken welke complexe vormen
verschillend zijn; maar, de vorm van het resultaat hangt af van de instelling in het
8 menu.
Invoer: Weergave: Omschrijving:
9 ()Stelt graden in.
z8
(T)
Stelt complexe stand in
{?
)θ)
)θ)
Invoer van L1
{?
)θ))))
)θ)¨
Invoer van L2.
{?
)θ)
)θ)¨
Voert L3 in en telt L2 + L3
op.
)θ)¨Telt L1 + L2 + L3
op.
{Õ§Scrollt het scherm om de
rest van het antwoord te
zien
y
185 lb 62
o
100 lb 261
o
170 lb 143
o
L1
L2
L3
x

Bewerkingen met complexe getallen 9-7
Evalueer 1i1+3
θ
10+5
θ
30
Complexe getallen in Vergelijkingen
U kunt complexe getallen als vergelijkingen intypen. Wanneer een vergelijking
wordt weergegeven, worden alle nummerieke vormen getoond zoals ze zijn
ingevoerd, zoals xiy, of rθ a
Wanneer u een vergelijking evalueert en gevraagd wordt om variabele waarden,
kunt u complexe getallen invoeren. De waarden en formaat van het resultaat
worden gecontroleerd door de scherminstelling. Dit is hetzelfde als rekenen in de
ALG stand.
Vergelijkingen die complexe getallen bevatten kunnen opgelost en geïntegreerd
worden.
Invoer: Weergave: Omschrijving:
9 ()Stelt graden in.
z8
(T)
Stelt complexe stand in
6 )θ)
)θ)
Invoer 1i1
{?
)θ)
)θ)
Invoer 3
θ
10
{?
)θ)
)θ)
Voert 5
θ
30 in en telt 3
θ
10 op.
)θ) Telt 1i1, resultaat is
9,2088
θ
25,8898

9-8 Bewerkingen met complexe getallen
Complex getal in een programma
In een programma, kunt u een complex getal invoeren. Bijvoorbeeld,1i2+3θ 10+5
θ 30 in een programma is:
Wanneer u bezig bent met een programma en wordt gevraagd voor waarden met
INPUT instructies, kunt u complexe getallen invoeren. De waarden en formaat van
het resultaat worden gecontroleerd door de scherminstelling.
Het programma dat een complex getal bevat kan worden opgelost en geïntegreerd.
Programmaregels: (ALG–stand) Omschrijving
Hier begint het programma
--
!

Vector berekening 10-1
10
Vector berekening
Vanuit een wiskundig standpunt gezien, is een vector een matrix van 2 of meer
elementen gerangschikt in een rij of kolom.
Natuurkundige vectoren die meer dan twee of drie componenten hebben en
natuurkundige hoeveelheden kunnen vertegenwoordigen zoals positie, snelheid,
acceleratie, krachten, momenten, linaire en hoekvormige impuls hoekvormige
positie en acceleratie,etc.
Een vector invoeren:
1. Druk op {3
2. Voer het eerste getal voor de vector in.
3. Druk opz en en voer een tweede getal in voor een 2–D of 3–D vector.
4. Druk opz en voer een derde getal in voor een 3–D vector.
De HP 35s kan geen vectoren hanteren met meer dan 3 dimensies.
Vectorbewerkingen
Optelling en aftrekking:
Het optellen en aftrekken van vectoren vereist dat twee vector operands dezelfde
lengte hebben. Pogingen om vectoren met verschillende lengtes op tellen en af te
trekken hebben als resultaat de foutmelding “# !”.
1. De eerste vector invoeren
2. De tweede vector invoeren
3. Druk op of
10-2 Vector berekening
Bereken [1,5,–2,2]+[–1,5,2,2]
Bereken [–3,4,4,5]–[2,3,1,4]
Vermenigvuldiging en deling met een scalair:
1. Voer een vector in
2. Voer een scalair in
3. Druk y voor vermenigvuldigen of p voor delen
Invoer: Weergave: Omschrijving:
9()Verandert in de RPN
stand (indien nodig)
{3z
_
<)8.)=
<)8.)=
Voert [1,5,–2,2]
{3_
z
<)8.)=
<.)8)=
Voert [–1,5,2,2]
)
<)8)=
Twee vectoren erbij
optellen
Invoer: Weergave: Omschrijving:
9()Verandert in de ALG
stand
{3_
zÕ
<.)8)=_Voert [–3,4,4,5]
{3
z
§)8)=.<)8)= Voert [2,3,1,4]
<.)8)=.<)8))
<.)8)=
Twee vectoren vanaf
trekken

Vector berekening 10-3
Bereken [3,4]x5
Bereken [–2,4]÷2
Absolute waarde van de vector
De absolute waarde functie “ABS”, wanneer toegepast op een vector, produceert
de grootte van de vector. Voor een vector A=(A1, A2,......An), wordt de grootte
omschreven als = .
1. Druk op{A
2. Voer een vector in
3. Druk op
Bijvoorbeeld: Absolute waarde van vector [5,12]:
{A{3z. Het antwoord is 13. In RPN:
9(){3z{A.
Invoer: Weergave: Omschrijving:
9()Verandert in de RPN stand
{3z
<)8)=
<)8)=
Voert [3,4]
<)8)=
_
Voert 5 als een scalair in
y)
<)8)=
Voert een
vermenigvuldiging uit
Invoer: Weergave: Omschrijving:
9()Verandert in de ALG stand
{3_z
Õ
<.8=_Voert [–2,4]
p <.8=ªVoert 5 als een scalair in
<.8=ª
<.)8)=
Voert een deling uit
A22
2
2
1n
AAA +⋅⋅⋅++
10-4 Vector berekening
Uitwendig product
De DOT functie wordt gebruikt om het uitwendig product van twee vectoren met
dezelfde lengte te berekenen. Pogingen om het uitwendig product van twee
vectoren met verschillende lengte te berekenen, krijgen een foutmelding “#
!” als resultaat.
Voor 2–D vectoren: [A, B], [C, D], wordt het uitwendig product bepaald als [A,
B][C, D]= A x C +B x D.
Voor 3–D vectoren: [A, B, X], [C, D, Y], wordt het uitwendig product bepaald als
[A, B, X][C, D, Y]= A x C +B x D+X x Y
1. De eerste vector invoeren
2. Druk op y
3. De tweede vector invoeren
4. Druk op
Let op: Het teken, y, betekent hier “uitwendig product” inplaats van “inwendig
product”. Voor inwendig product, zie hoofdstuk 17.
Berekent het uitwendig product van twee vectoren, [1,2] and [3,4]
Berekent het uitwendig product van twee vectoren, [9,5] and [2,2]
Invoer: Weergave: Omschrijving:
9()Verandert in de ALG stand
{3z
Õ
<8=_Voert de eerste vector in [1,2]
y{3z
<8=h<8= Voert y uit voor uitwendig
product en voert de tweede
vector in
) Het uitwendig product van
twee vectoren is 11
Invoer: Weergave: Omschrijving:
9()Verandert in de RPN stand
{3z
<)8)=
<)8)=
Voert de eerste vector [9,5]
{3z<)8)=
<8=
in en de tweede [2,2]

Vector berekening 10-5
Hoek tussen vectoren
De hoek van twee vectoren, A en B, kan gezien worden als
θ
=
ACOS(AB/ )
Vind de hoek tussen twee vectoren: A=[1,0],B=[0,1]
Vind de hoek tussen twee vectoren: A=[3,4],B=[0,5]
y) Drukt y voor uitwendig
product, en het uitwendig
product van twee vectoren is
28
Invoer: Weergave: Omschrijving:
9()Verandert in de ALG stand
9 ()Stelt de Gradenstand in
{O 12 Cosinus functie
{3z
Õ
1<8=2 Invoer van vector A [1,0]
y{3z
Õ
1<8=h<8=2 Invoer van vector B [0,1]
voor uitwendig product van
A en B
p{A{3
zÕ
§8=ª 1<8=2¨De hoeveelheid van vector
A [1,0]
p{A{3
z
§8=ª 1<8=2¨De hoeveelheid van vector
B [0,1]
1<8=h<)))
)
De hoek tussen twee
vectoren is 90
Invoer: Weergave: Omschrijving:
9()Verandert in de RPN stand
9()Stelt graden in.
{3z
{3z
y
)
Vindt het uitwendig product
van twee vectoren
BA

10-6 Vector berekening
Vectoren in Vergelijkingen
Vectoren kunnen in vergelijkingen gebruikt worden en in vergelijking variabelen
zoals echte nummers. Een vector kan ingevoerd worden als er gevraagd wordt om
een variabele.
Vergelijkingen die vectors bevatten kunnen opgelost worden, maar de oplosser is
beperkt in zijn mogelijkheden als de onbekende een vector is.
Vergelijkingen die vectors bevatten kunnen geintegreerd worden, maar het resultaat
van de vergelijking moet echt of een 1–D vector zijn of een vector met 0 als de
tweede en derde elementen.
{3z
{A
)
)
De hoeveelheid van vector
[3,4]
{3z
{A
)
)
De hoeveelheid van vector
[0,5]
y)
)
Vermenigvuldigt twee
vectoren
p
)
Deelt twee waarden
{O
)
De hoek tussen twee
vectoren is 36,8699

Vector berekening 10-7
Vectoren in Programma’s
Vectoren kunnen in een programma op dezelfde manier gebruikt worden als echte
en complexe getallen
Bijvoorbeeld, [5, 6] +2 x [7, 8] x [9, 10] in een programma is:
Een vector kan ingevoerd worden als er gevraagd wordt om een waarde voor een
variabele. Programma’s die vectors bevatten kunnen voor oplossen en integreren
gebruikt worden.
Programmaregels: Omschrijving:
Hier begint het programma
<8= - º <8= º<8= [5,6]
!

10-8 Vector berekening
Vectors creëren uit Variabelen of Registers
Het is mogelijk om vectoren te creëren die de inhouden van geheugen variabelen
bevatten, stapel registers of waarden van de indirecte registers, in start of
programmastand.
In de ALG stand, begin met het invoeren van de vector door op {3 te
drukken. De RPN werkt hetzelfde als de ALG stand, behalve dat de d toets
eerst ingedrukt moet worden, gevolgd door het indrukken van {3 .
Om een element in te voeren die een waarde bevat die is opgeslagen in een
geletterde variabele, druk h en de variabele letter.
Om een element in te voeren van een stapel register, druk de < toets en gebruik
de Õ of Ö toetsen om het onderstrepingsymbool te verplaatsen zodat het
onder het stapel register gebruikt kan worden en druk
Om een element in te voeren dat indirect is aangewezen door de waarde in het I of
J register, druk h en ofwel (I) of (J).
Bijvoorbeeld, om de vector [C,REGZ, (J)] in de RPN stand te construeren, druk
d{3 dan hCz<Õzh
A.

Conversies en berekeningen met talstelsels 11-1
11
Conversies en berekeningen met talstelsels
Het menu BASE ({ w) laat u getallen invoeren en de weergave van getallen
dwingen in decimale, binaire, octale en hexadecimale talstelsels.
Het menu LOGIC ({>) geeft toegang tot logische functies.
Het menu BASE
Menu label Omschrijving
De Decimale stand. Dit is de normale rekenmachine stand
% Hexadecimale stand. De HEX annunciator wordt
weergegeven als deze stand werkzaam is. Getallen
worden weergegeven in hexadecimaal formaat. In de
RPN stand ,reageren de toetsen N, Q, T,
<, 0 en 3 als een korte manier om de cijfers A tot
F in te voeren. In de ALG stand, druk K A, B, C, D, E
of F voor het invoeren van de cijfers A tot F.
! De Octale stand. De OCT annunciator wordt weergegeven
wanneer deze stand aktief is. Getallen worden
weergegeven in Octaal formaat.
De Binaire stand. De BIN annunciator wordt weergegeven
wanneer deze stand aktief is. Getallen worden
weergegeven in Binair formaat. Als een getal meer dan
12 cijfers heeft, kan met de {Õ en {Ö toetsen
het gehele getal gezien worden. (Zie “Vensters voor Lange
Binaire getallen” later in dit hoofdstuk.)
Ggeplaatst aan het eind van een getal betekent dat dit getal
een decimaal getal is
Kgeplaatst aan het eind van een getal betekent dat dit getal
een hexadecimaal getal is. Om een hexadecimaal getal
in te voeren, typ het getal gevolgd door “K”

11-2 Conversies en berekeningen met talstelsels
Voorbeelden: Het talstelsel van een getal converteren.
De volgende toetsen zorgen voor de conversies.
Converteer 125,9910 naar hexadecimaal, octaal, en binair.
Opmerking: Wanneer niet decimale talstelsels worden gebruikt, wordt alleen het
gehele deel van getallen gebruikt voor weergave. De gebroken delen worden
gehouden (tenzij bewerkingen worden uitgevoerd die ze wissen) en worden
weergegeven als het decimale talstelsel wordt geselecteerd.
Converteer 24FF16 naar binair. Het binaire getal is langer dan 14 cijfers (het
maximum op het scherm).
µgeplaatst aan het eind van een getal betekent dat dit getal
een octaal getal is. Om een octaal getal in te voeren, typ
het getal gevolgd door “µ”
Egeplaatst aan het einde van een getal betekent dat dit
getal een binair getal is. Om een binair getal in te voeren,
typ het getal gevolg door “E”
Invoer: Weergave: Omschrijving:
{w
(%)
K Converteert het decimaal getal
naar 16.
{w (!)µ Talstelsel 8.
{w ()E Talstelsel 2.
{w ())
Invoer: Weergave: Omschrijving:
{w (%)
33{
w (K)
K Gebruik de toets 3 om “F” in
te voeren.
Conversies en berekeningen met talstelsels 11-3
u kunt het w menu gebruiken voor het invoeren van het talstelsel –n teken b/o/
d/h gevolgd door de operand om het 2/8/10/16 talstelsel in elke base stand in te
voeren. Een getal zonder talstelsel teken is een decimaal getal
Opmerking:
In de ALG–stand:
1. De resultaat talstelsel wordt bepaald door de huidige talstelsel instelling.
2. Als er geen aktieve commandoregel is (er is geen blinkende cursor in regel 1),
zal het veranderen van het talstelsel de tweede regel opwaarderen voor een
nieuw talstelsel.
3. Na het indrukken van of het veranderen van het talstelsel, zal de
rekenmachine automatisch een huidig talstelsel teken toevoegen b/o/h
gevolgd door het resultaat voor talstelsel 2/8/16 in regel 2.
4. Om een expressie opnieuw te bewerken, druk Ö of Õ
In de RPN–stand:
Als u een getal in regel 2 invoert, druk op en verander dan het talstelsel,
de rekenmachine zal de talstelsel van de getallen converteren in regel 1 en regel 2,
en het teken b/o/h zal worden toegevoegd gevolgd door het getal voor het
talstelsel 2/8/16.
Om de volgende scherminhoud in regel 2 te kijken bekijken, druk op {Ö of
{Õ om het scherm te veranderen
{w ()
¨
Het gehele binaire getal past
niet op het scherm. De
annunciator ¨ wijst erop dat
het getal links nog langer is.
{Õ§EGeeft de rest van het getal
weer. Het gehele getal is
10010011111111b.
{Ö¨Geeft de eerste 14 cijfers weer.
{w()8) Terug naar decimaal.

11-4 Conversies en berekeningen met talstelsels
Het LOGIC Menu
De “NAND”, “NOR”, “AND”, “OR”, “XOR”, “NOT”, kunnen worden gebruikt als
logische functies.Breuk,complex,vecor argumenten zijn te zien als een “#
!” in een logische functie.
Rekenen met talstelsels 2, 8 en 16
U kunt berekeningen uitvoeren met gebruik van , , y en p in elk
talstelsel. De enige toetsen die niet bruikbaar zijn in de HEX stand zijn <, *,
-, 0, 3 en 6. Maar, u moet weten dat de meeste bewerkingen anders
dan aritmetisch geen bruikbare resultaten zullen opleveren aangezien de gebroken
delen van de getallen zijn afgekapt.
Het rekenen in de talstelsels 2, 8 en 16 werkt met 2’s complement en werkt alleen
met gehele getallen:
Heeft een getal een deel achter de komma, dan wordt dat genegeerd bij
rekenkundige bewerkingen.
Menu label Omschrijving
Logisch bit voor bit “AND” van twee argumenten.
Bijvoorbeeld: AND (1100b,1010b)=1000b
% Logisch bit voor bit “XOR” van twee argumenten.
Bijvoorbeeld: XOR (1101b,1011b)=110b
Logisch bit voor bit “OR” van twee argumenten.
Bijvoorbeeld: OR (1100b,1010b)=1110b
! Brengt het ene complement terug van het argument. Elke
bit in het resultaat is het complement van de
overeenstemmende bit in het argument.
Bijvoorbeeld: NOT (1011b)=
111111111111111111111111111111110100b
Logisch bit voor bit “NAND” van twee argumenten.
Bijvoorbeeld:
NAND(1100b,1010b)=11111111111111111111111
1111111110111b
Logisch bit voor bit “NOR” van twee argumenten.
Bijvoorbeeld: NOR (1100b,1010b)=
111111111111111111111111111111110001b
Conversies en berekeningen met talstelsels 11-5
Het resultaat van een bewerking is altijd een geheel getal. (Het deel achter
de komma wordt afgekapt).
Waar conversies alleen de weergave van het getal veranderen maar niet het echte
getal in het X–register, meldt aritmetisch het getal in het X–register.
Als het resultaat van een bewerking niet kan worden getoon in geldige bits, geeft
het scherm #$ weer en toont dan het grootste positieve of negatieve getal
mogelijk.
Voorbeeld:
Hier zijn een paar voorbeelden van berekeningen in Hexadecimaal, Octaal en
Binaire standen:
12F16 + E9A16 = ?
77608 – 43268 =?
1008 ÷ 58=?
5A016 + 10011002 =?
Invoer: Weergave: Omschrijving:
{w (%)Kiest hexadecimaal; de
annunciator HEX verschijnt.
3{w
(K)0N{
w (K)
K Resultaat.
{w (!)µ Stelt octaal in: Annunciator
OCT verschijnt. Weergegeven
getal wordt naar octaal
geconverteerd.
{w
(µ)
{ w (µ)
µ Resultaat.
{w
(µ){w
(µ) p
µ Het gehele deel van het
resultaat.
{w(%)
N{w
(K)
K Kiest hexadecimaal; de
annunciator HEX verschijnt.

11-6 Conversies en berekeningen met talstelsels
De representatie van getallen
Hoewel de weergave van een getal verandert als het talstelsel veranderd wordt,
verandert er niets aan de opgeslagen vorm van het getal. Decimale getallen
worden dus niet weergegeven — zolang ze niet worden gebruikt in berekeningen.
Is een getal hexadecimaal, octaal of binair, dan wordt het weergegeven met 36 bits
(12 octale cijfers of 9 hexadecimale cijfers). Voorloopnullen worden niet
weergegeven, maar ze zijn belangrijk omdat ze een positief getal aanduiden.
Bijvoorbeeld, de binaire representatie van 12510
wordt weergegeven als:
1111101b
en dat is hetzelfde als deze 36 cijfers:
000000000000000000000000000001111101b
Negatieve getallen
Het meest linkse bit (meest significant of “hoogste” bit) van een binair getal is het
tekenbit. Het is 1 bij negatieve getallen. Zijn er voorafgaande nullen (die niet
weergegeven worden), dan is het tekenbit 0 en het getal positief nul en het getal
positief. Een negatief getal is het 2’s complement van het tegengestelde getal.
{w ()
{ (E)
bStel binair in; annunciator
BIN verschijnt. Dit sluit de
cijferinvoer af, dus is
niet nodig tussen de getallen.
E Resultaat in binair.
{w (%)K Resultaat in hexadecimaal.
{w ()8) Herstelt de decimaal.
Invoer: Weergave: Omschrijving:
{w
(%)
K Geeft een positief decimaal
getal op en converteert het
naar hexadecimaal.

Conversies en berekeningen met talstelsels 11-7
Bereik van getallen
De lengte van 36 bits bepaald de lengte van getallen die hexadecimaal (9 cijfers),
octaal (12 cijfers) en binair (36 cijfers) kunnen worden opgeslagen, en het bereik
van decimale getallen (11 cijfers) die hiernaar geconverteerd kunnen worden.
Bereik van getallen voor conversies naar een ander talstelsel
Getallen buiten dit bereik kunnen niet worden ingevoerd wanneer een niet
decimaal getal is geselecteerd.
_
K 2’s complement (teken
veranderd).
{w ()¨Binair getal; ¨ betekent dat
er nog meer cijfers zijn. Het
getal is negatief want het
hoogste bit is 1.
{Õ§¨Geeft de rest van het getal
weer door het scrolllen van
een scherm
{Õ§E Geeft het meest rechtse
venster weer;
{w () .) Negatief decimaal getal.
Talstelsel Grootste positief getal Grootste negatief getal
Hexadecimaal 7FFFFFFFFh 800000000h
Octaal 377777777777o 400000000000o
Binair 0111111111111111111111
11111111111111b
10000000000000000000000
0000000000000b
Decimaal 34.359.738.367 –34.359.738.368
11-8 Conversies en berekeningen met talstelsels
In BIN/OCT/HEX, Als een getal ingevoerd in het decimale talstelsel buiten het
bereik bevalt van wat hierboven is vernoemd, dan krijg je het bericht ! te
zien. Elke bewerking met gebruik van ! veroorzaakt een overloop conditie
,welke het grootste positieve of negatieve getal vervangt voor een te groot getal.
Vensters voor lange binaire getallen
Het langste binaire getal heeft 36 cijfers. Elke 14– cijfer weergave van een lang
getal wordt een venster genoemd.
Is een binair getal groter dan 14 cijfers, dan verschijnt de annunciator § of ¨ (of
beide), die aangeeft in welke richting de extra cijfers zich bevinden. Druk op de
aangegeven toets ({Ö of {Õ) om de rest te zien.
Talstelsels gebruiken in programma en vergelijkingen
Vergelijkingen en programma zijn beïnvloed door de talstelsel instelling en binaire,
octale en hexadecimale getallen kunnen in vergelijking ingevoerd worden en ook in
programma als de rekenmachine vraagt om een variabele. Resultaten worden
getoond volgens het huidige talstelsel.
Getal van 36–bits
E
Hoog venster
(weergegeven)
Laagste venster
Druk om het linker
venster te tonen
{Ö{ÕDruk om het rechter
venster te tonen
§ ¨
E
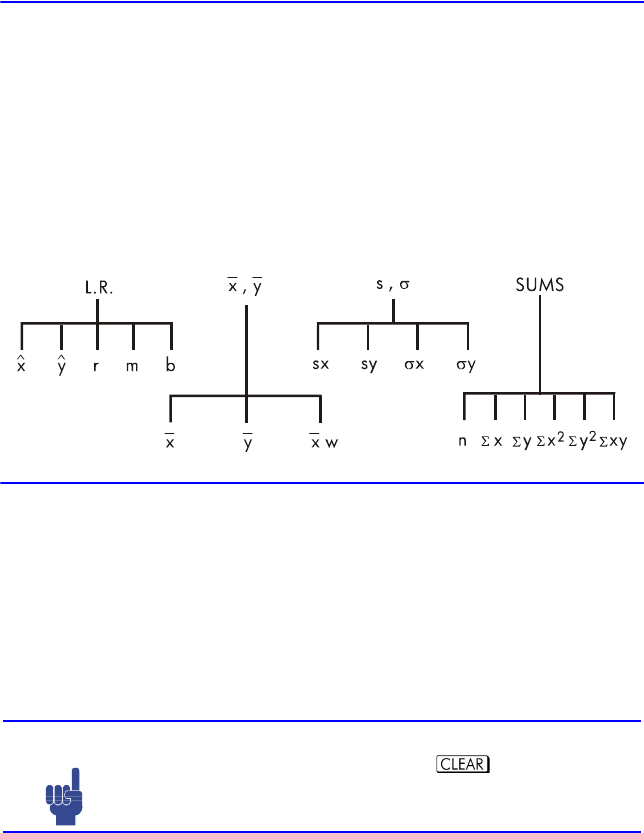
Statistische bewerkingen 12-1
12
Statistische bewerkingen
De statistische menu’s van de HP 35s bieden functies om gegevens met een of twee
variabelen statische te analyseren (echte getallen):
Gemiddelde afwijkingen en standaardafwijkingen van een steekproef en een
populatie.
Lineaire regressie en lineaire schatting ( en ).
Gewogen gemiddelde (x gewogen met y).
Statistische optellingen: n, Σx, Σy, Σx2, Σy2, en Σxy.
Statistische gegevens invoeren
Statistische gegevens met een of twee variabele voert u in (en verwijdert u) met de
toets 6 (of z4). De waarden worden geaccumuleerd als opgetelde
gegevens in zes statische registers (–27 tot en met –32), waarvan de namen
verschijnen in het menu SUMS. (Druk op {5 en zoek naar Q ;º ;¸ ;º
;¸ ;º¸).
Opmerking Maak altijd de statistische registers leeg voordat u nieuwe
gegevens gaat invoeren (druk op { (;)).
x
ˆy
ˆ

12-2 Statistische bewerkingen
Gegevens met één variabele invoeren
1. Druk op { (;) om de vorige statistische gegevens te wissen.
2. Geef iedere waarde van x op en druk op 6.
3. Het scherm toont n, het aantal statistische gegevens. De waarden worden nu
geaccumuleerd.
Door op 6 te drukken worden er eigenlijk twee waarden in de statistische
registers opgeslagen, want de waarde die toevallig in het Y–register staat wordt als
de y–waarde geaccumuleerd. Daardoor kan de rekenmachine lineaire regressie
uitvoeren en waarden weergeven die gebaseerd zijn op y, zelfs als u alleen maar
x–gegevens hebt ingevoerd — ja zelfs als u een ongelijk aantal x– en y–waarden
hebt ingevoerd. Er treedt geen fout op, maar de resultaten zijn natuurlijk niet zinvol.
Om een waarde in het scherm terug te roepen, drukt u direct nadat deze is
ingevoerd op {.
Gegevens met twee variabelen invoeren
Wanneer de gegevens een paar variabelen zijn ,voer dan eerst de afhankelijke
variabele in (de tweede variabele van het paar) en druk op , en voer dan
de onafhankelijke variabele in ( de eerste variabele van het paar) en druk op 6.
1. Druk op { (;) om de vorige statistische gegevens te wissen.
2. Geef eerst de y–waarde op en druk op .
3. Geef de overeenstemmende x–waarde op en druk op 6.
4. Het scherm toont n, het aantal statistische gegevensparen dat u hebt ingevoerd.
5. Ga door met het invoeren van x, y–paren, n wordt opgewaardeerd met elke
invoer.
Om direct na het invoeren een x–waarde terug te roepen, drukt u op {.
Fouten verbeteren in de gegevensinvoer
Maakt u een fout bij het invoeren van statistische gegevens, verwijder de fout dan
en geef de juiste gegevens op. Zelfs als van het x, y–paar maar een getal verkeerd
is, moet u beide gegevens opnieuw invoeren.

Statistische bewerkingen 12-3
Statistische gegevens corrigeren:
1. Voer de onjuiste gegevens opnieuw in, maar druk nu niet op 6, maar op
z 4. Hiermee worden de waarden verwijderd en wordt n verminderd.
2. Geef de juiste waarden op met 6.
Als de onjuiste gegevens diegene zijn die net zijn ingevoerd, druk dan op z
om ze terug te halen, en dan op z 4 om ze te verwijderen. (De
onjuiste y–waarde was nog in het Y–register en zijn x–waarde was opgeslagen in
de LAST X register). Na het wissen van de onjuiste statistische gegevens, zal de
rekenmachine de waarde van het Y–register tonen in regel 1 en de waarde van n in
regel 2.
Voorbeeld:
Geef de x, y onjuiste waarden links op, en corrigeer ze met de juiste waarden
rechts:
Initiaal x, y Gecorrigeerde x, y
20, 4 20, 5
400, 6 40, 6
Invoer: Weergave: Omschrijving:
{ (;) Wist de bestaande
statistische gegevens.
6 )
)
Voert het eerste nieuwe
gegevenspaar in.
6
)
)
Scherm toont n, het aantal
paren dat u heeft ingevoerd.
{ )
)
Haalt de laatste x–waarde
terug. De laatste y is nog in
het Y–register.
z4 )
)
Verwijdert het laatste paar.
6 )
)
Geeft het laatste paar
opnieuw op.
z
4
)
)
Verwijdert het eerste paar.
12-4 Statistische bewerkingen
Statistische berekeningen
Nadat u de gegevens hebt ingevoerd, kunt u de functies in de statistiekmenu’s gaan
gebruiken.
Statistiekmenu’s
Gemiddelde
Het gemiddelde is het wiskundige gemiddelde van een aantal getallen.
Druk op z/ ( ) voor het gemiddelde van de x–waarden.
Druk op z/Õ( ) voor het gemiddelde van de y–waarden.
Druk op z/ÕÕ() voor het gewogen gemiddelde van de x–
waarden, waarbij de y–values als gewicht gelden. De gewichten hoeven
geen gehele getallen te zijn.
6 )
)
Geeft het eerste paar
opnieuw op. Er staan nog
steeds twee paren in de
statistische registers.
Menu Toets Omschrijving
L.R. z ,Het menu voor lineaire regressie: lineaire
schatting en curve–fitting T P E. Zie
“Lineaire regressie” verderop in dit hoofdstuk.
,z /Het menu voor gemiddelden: .
Zie “Gemiddelde” hieronder.
s,σ{ 2Het menu voor de standaarddeviatie: Uº U¸
σº σ¸. Zie “Standaarddeviatie van
steekproef” en “Standaarddeviatie van
populatie” verderop in dit hoofdstuk.
SUMS { 5Het sommeringsmenu: Q ;º ;¸ ;º ;¸
;º¸. Zie “Statistieken sommeren” verderop in
dit hoofdstuk.
º
ˆ¸
ˆ
xyº ¸ ·º
º
¸
·º

Statistische bewerkingen 12-5
Voorbeeld: Gemiddelde (Eén variabele).
Productiechef May Kitt wil de gemiddelde duur van het productieproces weten. Ze
kiest zes willekeurige werknemers, observeert ze terwijl ze hun werk doen, en
noteert de volgende tijden (in minuten):
Bereken de gemiddelde tijdsduur. (Beschouw alle gegevens als x–waarden.)
Voorbeeld: Gewogen gemiddelde (Twee variabelen).
Een fabriek koopt vier keer per jaar een zeker onderdeel. In het vorige jaar waren
dat:
Bepaal de gemiddelde prijs (gewogen naar de aangekochte hoeveelheid) voor dit
deel. Denk eraan dat u eerst y, het gewicht (frequentie), en daarna x, de prijs,
opgeeft.
15,5 9,25 10,0
12,5 12,0 8,5
Invoer: Weergave: Omschrijving:
{ (;)Maakt de statistische registers
leeg.
6 ) Voert de eerste tijdsduur in.
6
66
66
)
Voert de overige gegevens in;
zes gegevens in totaal.
z/ ()
)
Berekent de gemiddelde
tijdsduur.
Stuksprijs (x) $4,25 $4,60 $4,70 $4,10
Aantal (y) 250 800 900 1000
Invoer: Weergave: Omschrijving:
{ (;)Maakt de statistische
registers leeg.
6
6
6
)
)
Voert gegevens in; toont n.
ºº ¸ ·º

12-6 Statistische bewerkingen
Standaardafwijking van een steekproef
De standaardafwijking van een steekproef geeft u een indruk hoe de waarden
rondom het gemiddelde verdeeld zijn. De standaardafwijking veronderstelt dat de
gegevens een steekproef zijn van een grotere hoeveelheid gegevens en wordt
berekend met n – 1 als deler.
Druk op {2 (Uº) voor de standaardafwijking van de x–waarden.
Druk op {2Õ (U¸) voor de standaardafwijking van de of y–
waarden.
De (σº) en (σ¸) items in dit menu worden beschreven in het volgende deel,
“Standaardafwijking van bevolking.”
Voorbeeld: Standaardafwijking van een steekproef.
Met dezelfde gegevens als hierboven in het voorbeeld “gemiddelde” wil May Kitt
de standaarddeviatietijd (sx) van het proces weten:
Bereken de standaardafwijking van de productietijden. (Beschouw alle gegevens
als x–waarden.)
6
8)
)
Vier paren geaccumuleerd.
z/ÕÕ ()
)
Berekent het gemiddelde,
gewogen naar de
aangeschafte hoeveelheid.
15,5 9,25 10,0
12,5 12,0 8,5
Invoer: Weergave: Omschrijving:
{ (;)Maakt de statistische registers
leeg.
6 ) Voert de eerste tijdsduur in.
6
66
66 )
Voert de overige gegevens in; zes
gegevens in totaal.
{ 2 (Uº)Uº U¸¦º¦¸
)
Berekent de standaardafwijking
van de productietijd.
·º º¸·º

Statistische bewerkingen 12-7
Standaardafwijking van bevolking
De standaardafwijking geeft aan hoe de gegevens rondom het gemiddelde
verdeeld zijn. Werken we met een bevolking, dan nemen we aan dat er geen
sprake is van een steekproef, maar dat alle gegevens bekend zijn. We gebruiken
nu n als deler.
Druk op { 2ÕÕ (σº) voor de standaardafwijking van een
bevolking van de x–waarden.
Druk op { 2ÕÕÕ (σ¸) voor de standaardafwijking van een
bevolking van de y–waarden.
Voorbeeld: Standaardafwijking van een bevolking.
Oma Hinkle heeft vier volwassen zoons met een lengte van 170, 173, 174 en 180
cm. Bepaal de standaardafwijking van deze lengtes.
Lineaire regressie
Lineaire regressie, L.R. (ook genoemd lineaire schatting) is een statistische methode
om een rechte lijn te vinden die het best overeenkomt met een reeks x, y–gegevens.
Invoer: Weergave: Omschrijving:
{ (;)Maakt de statistische registers
leeg.
6
66
6 )
Voert gegevens in. Vier
gegevenspunten zijn
geacummuleerd.
{ 2ÕÕ (σº)Uº U¸¦º¦¸
)
Berekent de standaardafwijking
van de bevolking.
Opmerking Om de melding !! te vermijden, moeten de
gegevens worden ingevoerd, voordat u een van de functies in
het menu L.R. uitvoert.

12-8 Statistische bewerkingen
Het menu L.R. (lineaire regressie)
Om een geschatte waarde te vinden voor x (of y), geeft u een hypothetische
waarde op voor y (of x) en drukt u op z, () (of z,Õ ().
Om de waarden te vinden die het best overeenkomen met de lijn die door uw
gegevens loopt, drukt u op z , gevolgd door T, P of E.
Voorbeeld: Curve Fitting.
De opbrengst van een nieuwe variëteit van rijst is afhankelijk van de bemesting met
stikstof. Bepaal de lineaire relatie tussen de volgende gegevens: de
correlatiecoëfficiënt, de helling, en de y–intercept.
Menutoets Omschrijving
Schat (voorspelt) x voor een gegeven hypothetische
waarde van y, gebaseerd op de lijn die uit de gegevens
is berekend.
Schat (voorspelt) y voor een gegeven hypothetische
waarde van x, gebaseerd op de lijn die uit de gegevens
is berekend.
TCorrelatiecoëfficiënt voor de (x, y)–gegevens. De
correlatiecoëfficiënt is een getal tussen –1 en +1 dat
aangeeft hoe goed de berekende lijn overeenkomt met de
gegevens.
PHelling van de berekende lijn.
Ey–intercept van de berekende lijn.
X, hoeveelheid stikstof
(kg per hectare)
0,00 20,00 40,00 60,00 80,00
Y, Graanopbrengst
(metrieke tonnen per
hectare)
4,63 5,78 6,61 7,21 7,78
Invoer: Weergave: Omschrijving:
{ (;)Wist de vorige statistische
gegevens.
º
ˆ
¸
ˆ
º
ˆ¸
ˆ
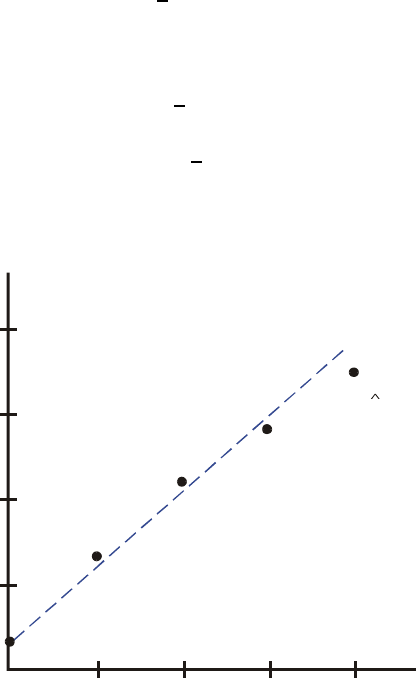
Statistische bewerkingen 12-9
6
6
6
6
)
)
Voert gegevens in; toont n.
6
)
)
Vijf paren gegevens ingevoerd.
z ,ÕÕ (T) T P E
)
Geeft het menu van de lineaire
regressie weer.
Correctiecoëfficiënt; gegevens
benaderen een rechte lijn.
Õ T P E
)
Richtingscoëfficiënt van de
regel.
Õ T P E
)
y–intercept.
º
ˆ¸
ˆ
º
ˆ¸
ˆ
º
ˆ¸
ˆ
x
0 20 40 60 80
8.50
7.5 0
6.50
5.50
4.50
r = 0.9880
m = 0.0387
b = 4.8560
(70, y)
y
X

12-10 Statistische bewerkingen
Stel dat er 70 kg stikstofmest wordt gebruikt? Voorspel de opbrengst op grond van
de bovenstaande statistiek.
Nauwkeurigheidsbeperkingen van de gegevens
De rekenmachine werkt met een beperkte precisie en dus zullen er afrondingsfouten
ontstaan. Hier zijn twee voorbeelden:
Normaliseren van dicht bijeenliggende, grote getallen
De rekenmachine is wellicht niet in staat de standaardafwijking en lineaire regressie
te herkennen voor een variabele waarvan de waarden relatief weinig verschillen.
Om dit te voorkomen, kunt u de gegevens normaliseren door iedere waarde in te
voeren als het verschil met een centrale waarde (bijvoorbeeld het gemiddelde).
Voor genormaliseerde x–waarden moet dit verschil achteraf worden opgeteld bij
een berekening van en , en en b moeten ook worden bijgesteld.
Bijvoorbeeld, als de x–waarden zijn 7776999, 7777000, en 7777001, dan geeft
u ze op als –1, 0 en 1; vervolgens telt u 7777000 op bij en . Voor b, telt u
7777000 x m bij. Om te berekenen geeft u een waarde van x op verminderd
met 7777000.
Soortgelijke onnauwkeurigheden kunnen optreden de waarden van x en y in een
heel andere orde van grootte liggen. Ook hier kan het wijzigen van de gegevens
het probleem voorkomen.
Effect van verwijderde gegevens
Met z 4 verwijdert u niet de afrondingsfouten die misschien in de statistische
registers zijn ontstaan. Het verschil is niet ernstig, tenzij de onjuiste gegevens
aanmerkelijk groter zijn dan de juiste gegevens. In dat geval is het wellicht
verstandig alle gegevens te wissen en opnieuw te beginnen.
Invoer: Weergave: Omschrijving:
)
_
Voert de hypothetische x–waarde in.
z ,Õ () T P E
)
Dit is de voorspelde opbrengst in
tonnen per hectare.
¸
ˆº
ˆ¸
ˆ
xx
ˆy
ˆ
xx
ˆ
y
ˆ

Statistische bewerkingen 12-11
Waarden in de statistische registers optellen
De statistische registers zijn zes unieke locaties in het geheugen waarin de
ingevoerde waarden worden geaccumuleerd.
Statistieken sommeren
Met { 5 hebt u toegang tot de inhoud van de statistische registers:
(Q) voor het oproepen van het getal van de ingevoerde data sets.
Druk op Õ (;º) om de som van de x–waarden op te roepen.
Druk op ÕÕ (;¸) om de som van de y–waarden op te roepen.
Druk op ÕÕÕ (;º), ÕÕÕÕ (;¸), en
ÕÕÕÕÕ (;º¸) om de som van de kwadraten en de som van
de producten van de x– en y—waarden op te roepen. Deze waarden zijn
van belang bij het uitvoeren van andere statistische berekeningen die door
de rekenmachine kunnen worden uitgevoerd.
Hebt u statistische gegevens ingevoerd, dan hebt u toegang tot de statistische
registers. Druk op zX(#) en gebruik × en Ø om de
statistische registers weer te geven.
Voorbeeld: De statistische registers bekijken.
Gebruik 6 om de paren (1,2) en (3,4) in de statistische registers op te slaan.
Bekijk nu de opgeslagen statische waarden.
Invoer: Weergave: Omschrijving:
{ (;)Maakt de statistische registers leeg.
6 )
)
Voert het eerste paar in (1,2).
6 )
)
Voert het tweede paar in (3,4).

12-12 Statistische bewerkingen
Toegang tot de statistische registers
De statistische register toekenningen in de HP 35s worden in de volgende tabel
getoond. Aan gesommeeerde registers moet gerefereerd worden bij de naam en
niet het getal in expressie, vergelijkingen en programma’s.
Statistische registers
z
X(#)
Q/ ©
) ª
Toont de VAR–catalogus en bekijkt
het register n.
×;º¸/ ©
) ª
Bekijkt het register Σxy.
×;¸/©
) ª
Bekijkt register Σy2.
×;º/©
) ª
Bekijkt register Σx2.
×;¸/ ©
) ª
Bekijkt register Σy.
×;º/ ©
) ª
Bekijkt register Σx.
×Q/ ©
) ª
Bekijkt register n.
)
)
Verlaat de VAR–catalogus.
Register Nummer Omschrijving
n–27 Aantal ingevoerde paren.
Σx–28 Som van de x–waarden.
Σy–29 Som van de y–waarden.
Σx2–30 Som van de kwadraten van de x–waarden.
Σy2–31 Som van de kwadraten van de y–waarden.
Σxy –32 Som van de producten van de x– en y–
waarden.
Statistische bewerkingen 12-13
U kunt een statistiekregister laden met een optelling door het nummer (–27 tot en
met –32) van het gewenste register op te slaan in i of J en daarna de optelling
opslaan (waarde H7 of A. U kunt verder drukken op z 7 of
A (K7 of A) om de waarde van een register te bekijken — naast de
waarde ziet u de naam van het register. Het menu SUMS bevat functies om de
waarden uit de registers op te roepen. Zie “Variabelen en labels indirect
adresseren” in hoofdstuk 14 voor meer informatie.

Deel 2
Programmeren

Eenvoudig programmeren 13-1
13
Eenvoudig programmeren
Deel 1 van deze handleiding toonde u de functies en bewerkingen die u handmatig
kunt invoeren, dat wil zeggen door voor iedere bewerking een toets in te drukken.
Verder hebt u gezien hoe u vergelijkingen kunt gebruiken om berekeningen te
herhalen zonder alle toetsen weer opnieuw te hoeven indrukken.
In deel 2 leggen we uit hoe u een programma kunt gebruiken voor herhaalde
berekeningen — berekeningen die ingewikkelder zijn dan een eenvoudige
vergelijking. Met een programma kunt u bewerkingen en berekeningen herhalen,
precies op de manier die u wilt.
In dit hoofdstuk leggen we uit hoe u een reeks bewerkingen programmeert. In het
volgende hoofdstuk, “Programmeringstechnieken”, leert u over subroutines en
voorwaardelijke instructies.
Voorbeeld: Een eenvoudig programma.
Om de oppervlakte te vinden van een cirkel met een straal van 5 gebruikt u de
formule A =
π
r2 en druk
RPN stand: 5 :z M y
ALG stand: 5 0 yz M
Om het resultaat te krijgen: 78,5398.
Maar als u nu de oppervlakte van een groot aantal verschillende cirkels wilt weten?
In plaats van de toetsaanslagen steeds te moeten herhalen (waarbij alleen de “5”
anders is voor de verschillende stralen), kunt u de toetsaanslagen in een
programma opnemen:

13-2 Eenvoudig programmeren
Dit eenvoudige programma veronderstelt dat de straal zich in het X-register (op het
scherm) bevindt als het programma start. De oppervlakte wordt berekend en in het
X-register gezet.
In de stand RPN voert u dit programma als volgt in het programmageheugen in:
Nu gaan we dit programma uitvoeren met een straal van 5:
In de ALG stand, om dit programma in het geheugen van de programma in te
voeren, doe het volgende:
RPN stand ALG stand
º 1º2ºπ
π
º
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
{
()Ö (&)
Maakt geheugen leeg.
{d Activeert de modus om een
programma in te voeren (de
annunciator PRGM verschijnt).
U ! Zet de programmawijzer op
PRGM TOP.
{: º(Straal)2
z M π
y ºOppervlakte =
π
x2
{ dBeëindigt de programma-invoer.
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
U Zet het programma aan het begin.
5 f) Het antwoord!
Invoer:
(In de ALG-stand)
Weergave: Omschrijving:
{
()Ö (&)
Maakt geheugen leeg.

Eenvoudig programmeren 13-3
Nu gaan we dit programma uitvoeren met een straal van 5:
We zullen dit programma verder gaan gebruiken om de verschillende conceptenen
methodes van het programmeren te bespreken.
Een programma ontwerpen
Hierna laten we zien welke instructies u in een programma kunt zetten. Wat u in
een programma zet heeft invloed op het resultaat als u het programma bekijkt en
op de werking als u het programma uitvoert.
Een stand selecteren
Programma’s gemaakt en opgeslagen in de RPN stand moeten bewerkt en
uitgevoerd worden in de RPN stand, en programma’s of stappen gemaakt en
opgeslagen in de ALG stand moeten bewerkt en uitgevoerd worden in de ALG
stand. Zoniet, dan is het resultaat niet juist.
{d Activeert de modus om een
programma in te voeren (de
annunciator PRGM verschijnt).
U ! Zet de programmawijzer op
PRGM TOP.
{:KXÕy
z M
1%2ºπOppervlakte =
π
x2
{ dBeëindigt de programma-invoer.
Invoer:
(In de ALG-stand)
Weergave: Omschrijving:
U Zet het programma aan het begin.
HX%
)
Slaat 5 op in X
f) Het antwoord!
13-4 Eenvoudig programmeren
Programmagrenzen (LBL en RTN)
Wilt u meer dan een programma in het geheugen zetten, dan heeft een programma
een label nodig om het begin te markeren (zoals ) en een return om
het einde te markeren (zoals !).
U ziet dat er bij de regelnummers een komt te staan die overeenkomt met het
label.
Programmalabels
Programma’s en segmenten van programma’s (routines) moeten met een label
beginnen. Als u een label wilt maken, drukt u op:
{ lettertoets
Het label is een willekeurige letter van A tot Z. De lettertoetsen worden gebruikt op
dezelfde manier als bij variabelen (zoals besproken in hoofdstuk 3). U hetzelfde
label niet meer dan een keer gebruiken (u krijgt dan de melding
"!)), maar een label kan zonder bezwaar dezelfde letter hebben
als een variabele.
Het is mogelijk dat een programma (het eerste) in het geheugen staat zonder label.
Alle volgende programma’s hebben echter een label nodig om ze van elkaar te
kunnen onderscheiden.
Programma’s kunnen niet meer dan 999 regels bevatten.
De return-instructie
Programma’s en subroutines moeten eindigen met een return-instructie. Deze voert u
in met:
z
Is een programma uitgevoerd, dan brengt de laatste RTN-instructie de
programmawijzer terug naar !, het begin van het programmageheugen.
Gebruik van RPN, ALG en vergelijkingen in programma’s
U kunt in een programma op dezelfde manier rekenen als met het toetsenbord:
Eenvoudig programmeren 13-5
Gebruik van RPN-bewerkingen (die werken met de stapel, zoals beschreven
in hoofdstuk 2).
Gebruik van ALG-bewerkingen (uitgelegd in aanhangsel C).
Gebruik van vergelijkingen (uitgelegd in hoofdstuk 6).
Het vorige voorbeeld gebruikte een reeks RPN-bewerkingen om de oppervlakte van
een cirkel te berekenen. U kunt ook een vergelijking gebruiken in het programma.
(Een voorbeeld ziet u later in dit hoofdstuk.) Veel programma’s zijn een combinatie
van RPN en vergelijkingen, met de voordelen van beide.
Voert een programma een regel uit met een vergelijking, dan wordt de vergelijking
op dezelfde manier geëvalueerd als met W. Bij de evaluatie in een programma
wordt “=” in een vergelijking beschouwd als “-”. (Er is geen programmeerbaar
equivalent voor in een toekenningsvergelijking — u moet dan de
vergelijking als expressie schrijven en STO gebruiken om het resultaat in een
variabele op te slaan.)
Bij beide soorten berekeningen kunt u RPN-instructies gebruiken om de invoer, de
uitvoer en het programmaverloop te besturen.
Invoer en uitvoer van gegevens
Heeft uw programma meer dan een invoerwaarde of meer dan een uitvoerwaarde,
dan kunt u zelf bepalen hoe het programma de invoer ontvangt en de uitvoer
presenteert.
Bij invoer kunt u om een waarde vragen met de INPUT-instructie. U kunt een
vergelijking gebruiken die om de waarde van een variabele vraagt, en u kunt
waarden gebruiken die tevoren op de stapel zijn gezet.
Voordelen van RPN-bewerkingen Voordelen van vergelijkingen
en ALG-bewerkingen
Gebruiken minder geheugen. Gemakkelijker te schrijven en te
lezen.
Voert sneller uit. Automatische prompts mogelijk.

13-6 Eenvoudig programmeren
Bij uitvoer kunt u de waarden presenteren met de VIEW-instructie. U kunt een bericht
tonen dat is afgeleid van een vergelijking, u kunt een proces presenteren in regel 1,
u kunt het programma resultaat in regel 2 presenteren en u kunt ongemarkeerde
waarden op de stapel laten staan.
Deze worden in dit hoofdstuk besproken onder “Gegevens invoeren en weergeven.”
Een programma invoeren
Met { d schakelt u de modus voor programmainvoer in en uit, zoals u ziet
aan de annunciator PRGM. Tijdens de invoer van een programma worden
toetsaanslagen opgeslagen in het geheugen als programmaregels . Iedere
instructie (commando) of expressie bezet een regel in het programma. In de ALG
stand, kunt u een expressie direct in het programma invoeren.
Een programma in het geheugen invoeren:
1. Druk op { d om de invoer van programma’s aan te zetten.
2. Druk op U om ! weer te geven. Dit zet de
programmawijzer op een bekende plek, vóór alle andere programma’s. Toetst
u nu programmaregels in, dan worden ze toegevoegd vóór alle andere
programmaregels.
Als u geen andere programma’s nodig hebt die in het geheugen kunnen zitten,
wis dan het geheugenprogramma door op { () te drukken,
Om te bevestigen dat u alle programma’s wilt verwijderen, druk op Ö (&)
na het bericht @ & .
3. Geef het programma een label — een enkele letter. Druk op { letter.
Kies een letter waarmee u de functie van het programma gemakkelijk kunt
onthouden, bijvoorbeeld een “A” voor de “oppervlakte.”
Als het bericht "!) wordt weergegeven, gebruik dan een
andere letter. U kunt altijd het bestaande programma wissen — druk op
zX(), gebruik × of Ø voor het vinden van het label, en
druk op { en .
4. Om bewerkingen met de rekenmachine als programma instructies op te slaan,
druk dezelfde toetsen als die u zou gebruiken voor een handmatige bewerking.
Onthoud dat veel functies niet op het toetsenbord verschijnen maar gebruikt
moeten worden met menu’s.
Voor het invoeren van een vergelijking in een programmaregel, zie
onderstaande instructies.

Eenvoudig programmeren 13-7
5. Beëindig het programma met een return-instructie, waarna de
programmawijzer terugkeert naar ! als het programma is
uitgevoerd. Druk op z.
6. Druk op (of {d) om de programma-invoer te beëindigen.
Getallen worden in een programmaregel precies zo opgeslagen als u ze invoert en
ze worden weergegeven met ALL of SCI. (Is een lang getal verkort weergegeven,
druk dan op z om alle cijfers weer te geven.)
Een vergelijking in een programmaregel opnemen:
1. Druk op G om de vergelijkingenstand te starten. De annunciator EQN
verschijnt.
2. Geef de vergelijking op dezelfde manier op als wanneer u met de
vergelijkingenlijst werkt. Zie hoofdstuk 6 voor details. Gebruik a om
typfouten te verbeteren.
3. Druk op om de vergelijking af te sluiten en het linkerdeel ervan weer
te geven. (De vergelijking komt niet in de vergelijkingenlijst.)
Nadat u een vergelijking hebt ingevoerd, drukt u op z om de
controlesom en lengte te zien. De waarden blijven op het scherm zolang u de toets
vasthoudt.
Is de vergelijking lang, dan verschijnen de annunciators ¨ en § om aan te geven
dat verschuiven voor deze programmaregel actief is. Met {Ö en {Õ kunt
u het beeld verschuiven.
Functies wissen en backspace toets
Let bij de programma-invoer op de volgende voorwaarden:
beëindigt altijd de programma-invoer. Het maakt nooit een getal nul.
In de programmaregel viewstatus, verwijdert a de huidige
programmaregel en begint Ö/Õ met de bewerkingsstatus. In
programmaregel bewerken status, verwijdert a het teken voor de cursor.
Om een functie te programmeren die het X-register leegmaakt, gebruikt u
{ (º).
Wanneer u een regel in een programma invoert of verwijdert, worden GTO en XEQ
verklaringen automatisch opgewaardeerd als het nodig is.
Bijvoorbeeld:

13-8 Eenvoudig programmeren
-
-
!
Wis nu regel A002, en regel A004 verandert in “A003 GTO A002”
Functienamen in programma’s
De naam van een functie die in een programma wordt gebruikt is niet noodzakelijk
gelijk aan het opschrift van de toets, de naam in het menu of in een vergelijking. De
naam die in een programma wordt gebruikt is gewoonlijk een langere afkorting
van de naam die op een toets of in een menu past.
Voorbeeld: Een gelabeld programma invoeren.
Met de volgende toetsen verwijdert u het vorige programma voor de oppervlakte
van een cirkel en maakt u een nieuw programma met een label en een return-
instructie. Maakt u tijdens de invoer een fout, druk dan op a om de regel te
verwijderen en geef daarna de juiste programmaregel op.
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
{d Start de invoer van een
programma (PRGM
verschijnt).
{
() Ö(&)
!
Maakt het
programmageheugen leeg.
{A
Geeft deze routine een
label A (van “oppervlakte”).
{:
zM
y
º
π
º
Voert de drie
programmaregels in.
z ! Beëindigt het programma.
zX (2)
/
Toont label A en de lengte
van het programma in
bytes.
z /
/
Controlesom en lengte van
het programma.
Eenvoudig programmeren 13-9
Een afwijkende controlesom betekent dat het programma niet precies is ingevoerd
als het hier staat.
Voorbeeld: Een programma met een vergelijking invoeren.
Het volgende programma berekent de oppervlakte van een cirkel met een
vergelijking, in plaats van met RPN zoals in het vorige programma.
Beëindigt de programma-
invoer (De annunciator
PRGM verdwijnt).
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
{dU
! Start de programma-invoer
en zet de wijzer bovenaan.
{E Geeft deze routine een
label E (van “vergelijking”).
{HR ! Slaat de straal op in de
variabele R
Gz M
y KR
0 πº:
Selecteert invoer van een
vergelijking; voert de
vergelijking in en gaat
terug naar programma-
invoer.
z /
/
z ! Beëindigt het programma.
zX (2)
/
Toont label E en de lengte
van het programma in
bytes.
z /
/
Controlesom en lengte van
het programma.
Beëindigt de programma-
invoer.

13-10 Eenvoudig programmeren
Een programma uitvoeren
Om een programma uit te voeren moet de programma-invoer niet actief zijn, er
worden dus geen regelnummers weergegeven en de annunciator PRGM is uit).
Door te drukken op beëindigt u de programma-invoer.
Een programma uitvoeren (XEQ)
Druk het W label om het programma uit te voeren dat is gelabeld met die letter:
Om een programma vanaf het begin uit te voeren druk op W label .
Bijvoorbeeld, druk WA Het scherm toont nu “% ” en de
uitvoering begint bovenaan op Label A.
U kunt ook een programma uitvoeren, beginnend vanuit een andere positie door het
indrukken van het
W
label Regelnummer, bijvoorbeeld
W
.
Als er maar een programma in het geheugen aanwezig is, kunt u het ook uitvoeren
na het verplaatsen van de wijzer naar de bovenste programmaregel en door op
f te drukken (run/stop) toets. De PRGM annunciator wordt getoond en de ¢
annunciator gaat aan terwijl het programma loopt.
Geef zonodig de invoergegevens op, voordat u het programma start.
Voorbeeld:
Start de programma’s A en E om de oppervlakten te berekenen van drie
verschillende cirkels met een straal van 5, 2,5, en 2π. Denk eraan dat u de straal
moet invoeren voordat u A of E start.
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
WA"
)
Voert de straal in en start
programma A. De oppervlakte
wordt getoond.
WE
) Berekent de oppervlakte van de
tweede cirkel met programma E.
z M y
WA)
Berekent de oppervlakte van de
derde cirkel.
Eenvoudig programmeren 13-11
Een programma testen
Als u weet dat er een fout zit in uw programma, maar niet waar, dan kunt u het
programma testen door het stap voor stap uit te voeren. Het is trouwens verstandig
een lang of gecompliceerd programma altijd van te voren te testen. Door de
programmaregels een voor een uit te voeren, ziet u het resultaat van iedere
programmaregel, zodat u kunt zien hoe correcte invoergegevens leiden tot een
eindresultaat.
1. Evenals bij het gewone uitvoeren moet de programma-invoer niet ingeschakeld
zijn (De annunciator PRGM is niet zichtbaar).
2.Zet de programmawijzer aan het begin van het programma (dat is, aan zijn
LBL instructie). De instructie beweegt de programmawijzer zonder te beginnen
met uitvoeren.
3. Houd Ø ingedrukt. U ziet nu de huidige programmaregel. Laat u Ø los,
dan wordt de regel uitgevoerd. Het resultaat wordt weergegeven (het staat in
het X-register).
Om naar de vorige regel te gaan, drukt u op ×. Er wordt niets uitgevoerd.
4. De programmawijzer gaat naar de volgende regel. Herhaal stap 3 tot u een
fout vindt (een onjuist resultaat) of het einde van het programma bereikt.
Is de programma-invoer actief, dan verandert u met Ø of × alleen de
programmawijzer, zonder iets uit te voeren. Houdt u tijdens de programma-invoer
een cursortoets ingedrukt, dan schuiven de regels automatisch voorbij.
Voorbeeld: Een programma testen.
Ga stap voor stap door de uitvoering van het programma met het label A. Gebruik
een straal van 5 om de gegevens te testen. Controleer voordat u begint of de
programma-invoer niet actief is:
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
U ) De programmawijzer gaat naar
label A.
Ø (vasthouden) (loslaten)
)
Ø (vasthouden) (loslaten) º
)
Kwadraat van invoer.

13-12 Eenvoudig programmeren
Gegevens in-en uitvoeren
De variabelen van de rekenmachine dienen om invoer, tussenresultaten en
eindresultaten op te slaan. (Variabelen, zoals uitgelegd in hoofdstuk 3, worden
geïdentificeerd door een letter van A tot Z, maar die namen hebben niets te maken
met de programmalabels.)
In een programma, kunt u op de volgende manieren gegevens invoeren:
Met een INPUT-instructie, waarbij om de waarde van een variabele wordt
gevraagd. (Dit is de handigste methode.)
Met de stapel. (U kunt STO gebruiken om een waarde in een variabele op te
slaan.)
Met variabelen waarin al waarden zijn opgeslagen.
Met automatische invoer in een vergelijking (indien dit is ingeschakeld met
flag 11). (Dit is ook handig als u met vergelijkingen werkt.)
In een programma kunt u op de volgende manieren gegevens uitvoeren:
Met een VIEW-instructie die de naam en de waarde van een variabele toont.
(Dit is de handigste methode.)
Met de stapel — alleen de waarde in het X en Y register is zichtbaar — (Met
PSE stopt de uitvoering voor een seconde, zodat u de waarde kunt zien.)
In een weergegeven vergelijking (indien dit is ingeschakeld met 10). (De
“vergelijking” is meestal een bericht, geen echte vergelijking.)
Enkele van deze technieken worden hieronder beschreven.
Ø (vasthouden) (loslaten) π
)
Waarde van
π
.
Ø (vasthouden) (loslaten) º
)
25
π
.
Ø (vasthouden) (loslaten) !
)
Einde van programma.
Resultaat is juist.

Eenvoudig programmeren 13-13
INPUT gebruiken voor invoer
De INPUT-instructie (z variabele ) stopt een lopend programma en toont
een prompt voor de gegeven variabele. U ziet hier ook de oude waarde van de
variabele, zoals
@
)
waarin
“R” de naam is van de variabele,
“?” de prompt voor invoer,
0,0000 de huidige waarde van de variabele.
Druk op f (run/stop) om het programma te hervatten. De ingevoerde waarde
vervangt de inhoud van het X-register en wordt opgeslagen in de gegeven
variabele. Hebt u de weergegeven waarde niet veranderd, dan blijft die waarde in
het X-register.
Met een INPUT-instructie ziet het programma voor de oppervlakte van een cirkel er
zo uit:
INPUT gebruiken in een programma:
1. Stel vast welke waarden u nodig hebt en ken er namen aan toe.
(In het voorbeeld van de cirkel hebt u alleen de straal nodig en daaraan kent u
de letter R toe.)
RPN stand ALG stand
"!
º
π
º
!
"!
12ºπ
!
13-14 Eenvoudig programmeren
2. Zet aan het begin van het programma een INPUT-instructie voor iedere
variabele waarvan u de waarde nodig hebt. Later in het programma, als u het
deel schrijft waarin de waarde nodig is, schrijft u de instructie K variabele
om die waarde weer in de stapel terug te roepen.
Omdat de instructie INPUT de ingevoerde waarde ook in het X-register laat
staan, hoeft u de waarde nu niet meer op te roepen—deze na INPUT meteen
klaar voor gebruik. Daardoor kunt u misschien wat geheugen besparen. In een
lang programma is het echter beter eerst alle gegevens in te voeren, en ze pas
op te roepen als ze nodig zijn.
Denk er ook aan dat de gebruiker van het programma ook berekeningen kan
uitvoeren terwijl het programma onderbroken is en op invoer wacht. Hiermee
kan hij de inhoud van de stapel wijzigen, wat weer invloed heeft op de
volgende berekening. Het is dus beter niet te veronderstellen dat de X-, Y-, en Z-
registers van de stapel voor en na de INPUT-instructie onveranderd zijn. Vraagt
u alle benodigde gegevens meteen aan het begin van het programma met de
bedoeling ze weer op te roepen als ze nodig zijn, dan verhindert u dat de
inhoud van de stapel onbedoeld veranderd wordt.
Antwoorden op een prompt:
Voert u het programma uit, dan stopt het bij iedere INPUT waar gevraagd wordt om
de variabele, bijvoorbeeld @). De weergegeven waarde (en de inhoud
van het X-register) is de huidige inhoud van R.
Om het getal onveranderd te laten, druk op f.
Om het getal te veranderen, typ het nieuwe getal in en druk op f. Dit
nieuwe getal overschrijft de oude waarde in het X-register. U kunt een getal
als een breuk invoeren als u dat wilt. Als u een getal moet berekenen, doe het
dan met normale toetsenbordberekeningen, druk dan op f. Bijvoorbeeld,
u kunt 0 f drukken in de RPN stand, of 0
f drukken in de ALG stand (Voordat u op drukt, zal
de expressie getoond worden in regel 2. Nadat u op gedrukt heeft,
zal het resultaat van de expressie de weergegeven expressie in regel 2
vervangen en worden opgeslagen in het X- register).

Eenvoudig programmeren 13-15
Om de INPUT-prompt te annuleren, drukt u op . De huidige waarde van
de variabele blijft in het X-register. Drukt u op f om het programma te
hervatten, dan ziet u opnieuw de INPUT-prompt. Drukt u op tijdens het
invoeren van een getal, dan wordt het getal nul. Door opnieuw op te
drukken annuleert u de INPUT-prompt.
VIEW gebruiken voor het weergeven van gegevens
De geprogrammeerde VIEW-instructie (z variabele ) stopt een lopend
programma en toont de inhoud van een gegeven variabele, zoals
/
)
Dit is alleen weergave, de inhoud van het X-register verandert niet. Staat de
weergave van breuken aan, dan wordt de waarde als breuk weergegeven.
Met kopieert u dit getal naar het X-register.
Als het getal meer dan 14 tekens heeft, zoals binair, complex, vector
getallen, druk op {Ö en {Õ toont de rest.
Drukt u op (of a) dan wordt de VIEW-weergave gewist en ziet u weer
het X-register.
Door te drukken op { verwijdert u de inhoud van de weergegeven
variabele.
Druk op f om het programma voort te zetten.
Als u niet wilt dat het programma stopt, zie dan “Informatie weergeven zonder
stoppen” hieronder.
Zie bijvoorbeeld het programma voor “Normale en inverse verdelingen” in
hoofdstuk 16. De regels T015 en T016 aan het einde van de routine T tonen het
resultaat van X. U ziet dat de VIEW-instructie in dit programma wordt voorafgegaan
door een RCL-instructie. Dat is niet nodig, maar plezierig omdat het de
weergegeven waarde naar het X-register kopieert, zodat deze voor verdere
handmatige berekeningen beschikbaar is. (Drukt u op terwijl de variabele
op het scherm staat, dan heeft dat hetzelfde effect.) De andere
toepassingsprogramma’s in hoofdstukken 16 tot en met 17 zorgen er ook voor dat
de VIEW-variabele in het X-register komt — met uitzondering van het programma
dat wortels van veeltermen vindt.

13-16 Eenvoudig programmeren
Vergelijkingen gebruiken om berichten weer te geven
Vergelijkingen worden niet gecontroleerd op de juiste syntaxis als ze niet
geëvalueerd worden. Dat betekent dat u bijna iedere reeks tekens als iedere andere
vergelijking kunt invoeren — u toetst ze op dezelfde manier in als een vergelijking.
Op een programmaregel drukt u op G om de vergelijking te starten. Met cijfer-
en functietoetsen krijgt u cijfers en symbolen. Druk op K voor iedere letter. Druk
op om de vergelijking te besluiten.
Is flag 10 gezet, dan worden de vergelijkingen niet geëvalueerd maar
weergegeven. Dat betekent dat u een bericht kunt weergeven door het als
vergelijking in te voeren. (Flags worden besproken in hoofdstuk 14.)
Wordt het bericht weergegeven, dan stopt het programma— druk op f om
verder te gaan. Is het weergegeven bericht langer dan 14 tekens, dan verschijnt de
annunciator ¨. U kunt dan { Õ en { Ö gebruiken om de rest te zien.
Als u niet wilt dat het programma stopt, zie dan “ Informatie weergeven zonder
stoppen” hieronder.
Voorbeeld: INPUT, VIEW en berichten in een programma.
Schrijf een vergelijking om de oppervlakte en de inhoud te vinden van een cilinder
waarvan de straal en de hoogte gegeven zijn. Noem het programma C (van
cilinder), en gebruik de variabelen S (oppervlakte), V (inhoud), R (straal), en H
(hoogte). Dit zijn de formules:
V =
π
R2H
S = 2
π
R2 + 2
π
RH = 2
π
R ( R + H )
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
{ d{
()
Ö1&2
!
Programma, invoer; wist het
programmageheugen.
{ Geeft het programma een
naam.
z ÇR "!
z ÇH "! Instructies om de straal en de
hoogte te vragen.
Eenvoudig programmeren 13-17
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
Gz M y
KR 0 y
KH
πº:º
Berekent de inhoud.
z /
/
Controlesom en lengte van de
vergelijking.
HV ! #Slaat de inhoud op in V.
G yz
MyKRy
4 KR
KH ºπºº1-¨
Berekent de oppervlakte.
z /
/
Controlesom en lengte van de
vergelijking.
HS ! Slaat de oppervlakte op in S.
z x
( )
Zet flag 10 om vergelijkingen
weer te geven.
G KV
KO KL
{o{
o KA
KR KE
KA # - ¨
Geeft bericht als vergelijking
weer.
z x
()
Wist flag 10.
z V #$ #Geeft de inhoud weer.
z S #$ Geeft de oppervlakte weer.
z ! Beëindigt het programma.
z X
()
/
Toont label C en de lengte
van het programma in bytes.
z /
/
Controlesom en lengte van
het programma.
Beëindigt de programma-
invoer.
13-18 Eenvoudig programmeren
Bepaal nu de inhoud en de oppervlakte van een cilinder met een straal van 2 1/2
cm en een hoogte van 8 cm.
Gegevens weergeven zonder te stoppen
Normaliter stopt een programma als er een vergelijking of een variabele met VIEW
wordt weergegeven. U moet dan op f drukken om verder te gaan.
Als u wilt, kunt u het programma verder uitvoeren, terwijl de gegevens op het
scherm staan. Bevat de volgende programmaregel — na VIEW of na een getoonde
vergelijking — een PSE (pauze) instructie, dan wordt de informatie weergegeven en
gaat het uitvoeren verder na een pauze van 1 seconde. In dit geval is schuiven niet
mogelijk en invoer via het toetsenbord ook niet.
Het beeld wordt leeggemaakt door andere weergaven en door de bewerking RND
als flag 7 gezet is (afronden naar een breuk).
Druk op { e om PSE in een programma op te nemen.
De regels VIEW en PSE of de vergelijking en PSE worden als één instructie
beschouwd, als u het programma regel voor regel uitvoert.
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
WC@
waarde
Starts het programma C; vraagt
om R. (De toevallige vorige
waarde van R wordt getoond
R.)
f
@
waarde
Voert 2 1/2 als breuk in. Vraagt
om H.
f # - Bericht wordt weergegeven.
f#/
)
Inhoud in cm3.
f /
)
Oppervlakte in cm2.

Eenvoudig programmeren 13-19
Een programma stoppen of onderbreken
Een stop of pauze programmeren (STOP, PSE)
Drukt u op f (run/stop) tijdens het invoeren van een programma, dan
wordt er een STOP-instructie ingevoegd. Deze geeft de inhoud van het X-
register weer en onderbreekt het programma tot u het weer hervat door op
f te drukken. U kunt STOP gebruiken in plaats van RTN om een
programma te beëindigen zonder dat de programmawijzer weer naar het
begin verplaatst.
Drukt u tijdens het invoeren van een programma op { e dan wordt er
een PSE-instructie (pauze) ingevoegd. Deze onderbreekt een lopend
programma en toont het X-register gedurende 1 seconde — met de volgende
uitzondering. Wordt PSE direct gevolgd door een VIEW-instructie of een
vergelijking die weergegeven wordt (flag 10 gezet), dan wordt die variabele
of vergelijking weergegeven — en de weergave blijft na de pauze van één
seconde staan.
Een lopend programma onderbreken
U kunt een lopend programma op ieder moment onderbreken door te drukken op
of f. Het programma maakt de huidige instructie af voordat het stopt. Druk
op f (run/stop) om het programma te hervatten.
Onderbreekt u een programma en drukt u daarna op W, U, of z ,
dan kunt u het programma niet meer hervatten met f. Het kan alleen alleen
opnieuw gestart worden met (W regelgetal).
Fouten in programma’s
Treedt er een fout op tijdens de uitvoering van een programma, dan stopt de
uitvoering en wordt er een foutmelding getoond. (Een lijst van foutmeldingen en
condities vindt u in aanhangsel F.)
Wilt u weten in welke programmaregel de fout optrad, druk dan op { d.
Dat is de instructie die de fout veroorzaakte. Het zou een ÷ kunnen zijn, die een
deling door nul probeerde uit te voeren.)

13-20 Eenvoudig programmeren
Een programma bewerken
U kunt een programma in programmageheugen wijzigen door het invoeren,
verwijderen en bewerken van programmaregels. Als een programmaregel een
vergelijking bevat, kunt u de vergelijking bewerken.
Een programmaregel verwijderen:
1. Selecteer het gewenste programma of routine, en druk op Ø of × om de
programmaregel te vinden die gewijzigd moet worden. Houd de cursortoets
ingedrukt om door de regels te bladeren.
2. Verwijder de regel die u wilt veranderen., druk dan direct op a (de Undo
functie is aktief). De wijzer gaat nu naar de vorige regel. (Verwijdert u
meerdere opeenvolgende regels, begin dan met de laatste in de groep.)
3. Toets de eventuele nieuwe instructie in. Deze vervangt de verwijderde
instructie.
4. Sluit de programma-invoer af ( of { d).
Een programmaregel toevoegen:
1. Zoek de programmaregel voor de plek waar u een regel wilt invoegen.
2. Voer de nieuwe instructie in. Deze komt na de weergegeven regel te staan.
Bijvoorbeeld, u wilt iets invoegen tussen regel A004 en A005 van een programma.
Ga nu eerst naar regel A004 en voer de nieuwe instructie(s) in. De daarop
volgende programmaregels, te beginnen met de oorspronkelijke regel A005,
schuiven naar beneden en krijgen een nieuw nummer.
Een operand, expressie of vergelijking bewerken in een programmaregel:
1. Bepaalt of toont de programmaregel die u wilt bewerken.
2. Druk op Õ of Ö om te beginnen met het bewerken van de
programmaregel. Deze stelt de “_” bewerkingscursor in werking, maar
verwijdert niets in de programmaregel.
De Õ toets verplaatst de cursor naar links van de programmaregel
De Ö toets verplaatst de cursor naar het einde van de programmaregel.

Eenvoudig programmeren 13-21
3. Beweeg met de cursor “_” en druk herhaaldelijk op a om het ongewenste
getal of functie te verwijderen, typ dan rest van de programmaregel opnieuw
in. ( Na het drukken op a, is de Undo functie aktief).
Mededeling:
1. Als de cursor aktief is in de programmaregel, is de Ø of × toets niet
werkzaam.
2. Wanneer u een programmaregel bewerkt (cursor aktief), en de
programmaregel is leeg, zal a gebruiken geen effect hebben. Als u de
programmaregel wilt wissen, druk dan op en de programmaregel
wordt gewist.
3. U kunt de {Õ en {Ö toetsen gebruiken om lange programmaregels
door te nemen zonder ze te bewerken.
4. In de ALG stand, kan niet als een functie gebruikt worden, het wordt
gebruikt om een programmaregel te valideren.
5. Een vergelijking kan in elke modus worden bewerkt ongeacht in welke modus
ze was ingevoerd.
Programmageheugen
Programmageheugen bekijken
Drukt u op { d dan wordt de programma-invoer uit- en aangezet (De
annunciator PRGM verschijnt en u ziet programmaregels). Is de programmainvoer
actief, dan wordt de inhoud van het programmageheugen weergegeven.
Het programmageheugen begint bij !. De lijst van programmaregels is
circulair, dus de programmawijzer gaat van de laatste regel naar de eerste en
andersom. Tijdens de programma-invoer zijn er vier manieren om de
programmawijzer (de weergegeven regel) te wijzigen:
{× en {Ø laten u zich verplaatsen van label naar labels. Als er
geen labels bepaald zijn, zal het naar boven of onderaan het programma
gaan.
Om snel naar een andere regel te gaan (“schuiven”), houdt u de toets Ø of

13-22 Eenvoudig programmeren
× ingedrukt.
Druk op U om de programmawijzer op ! te zetten.
Druk op U om de periodieke interest te berekenen.
Is de programma-invoer niet actief (er worden geen programmaregels
weergegeven), dan kunt u ook de programmawijzer verplaatsen met U label.
Door de programma-invoer te beëindigen verandert de waarde van de
programmawijzer niet.
Geheugengebruik
Krijgt u tijdens het invoeren van een programma de melding & ", dan
is er niet genoeg ruimte in het programmageheugen voor de regel die u wilt
invoeren. U kunt meer ruimte maken door andere programma’s of andere gegevens
te verwijderen. Zie “Een of meer programma’s wissen” hieronder, of “Het geheugen
beheren” in aanhangsel B.
De catalogus van programma’s (MEM)
De catalogus van programma’s is een lijst met alle programmalabels, inclusief het
aantal bytes dat voor ieder label nodig is en de regels die erbij horen. Druk op
z X(2) om de catalogus weer te geven en op Ø of × om door
de lijst te bladeren. Dit kunt u met de catalogus doen:
Labels in het programmageheugen bekijken met het geheugengebruik van
ieder programma en iedere routine.
Een programma uitvoeren. (Druk op W of f terwijl het label op het
scherm staat.)
Een programma weergeven. (Druk op { d terwijl het label op het
scherm staat.)
Programma’s verwijderen. (Druk op { terwijl het label op het
scherm staat.)
De controlesom van een stuk programma bekijken. (Druk op z .)
De catalogus toont hoeveel bytes ieder programma in beslag neemt. De
programma’s zijn te herkennen aan de labels:

Eenvoudig programmeren 13-23
/
waarin 67 het aantal bytes is dat het programma gebruikt.
Een of meer programma’s wissen
Een specifiek programma uit het geheugen verwijderen
1. Druk op z X (2) en geef (met Ø en ×) het label
van het programma weer.
2. Druk op { .
3. Druk op om de catalogus te annuleren of op a als u van gedachten
verandert.
Alle programma’s uit het geheugen verwijderen:
1. Druk op { dom de programmaregels weer te geven (De annunciator
PRGM staat aan).
2. Druk op { () om het programmageheugen leeg te maken.
3. Het bericht @ & vraagt om bevestiging. Druk op Ö (&) .
4. Druk op { d om de programma-invoer te beëindigen.
Het verwijderen van het ({ ()) geheugen verwijdert ook alle
programma’s.
De controlesom
De controlesom is een unieke hexadecimale waarde die aan ieder programmalabel
en de bijbehorende regels (tot het volgende label) wordt toegevoegd. Dit getal is
bruikbaar om te vergelijken met de bekende controlesom van een bestaand
programma, bijvoorbeeld als u het uit een boek hebt overgetypt. Komt de
controlesom in het boek overeen met de controlesom op de rekenmachine, dan hebt
u het programma foutloos ingevoerd. Dit doet u om de controlesom te zien:
1. Druk op z X () voor de catalogus van
programmalabels.
2. Geef het gewenste label met de cursortoetsen weer.
3. Houd z ingedrukt om / controlesom en / lengte te tonen.

13-24 Eenvoudig programmeren
Bijvoorbeeld, de controlesom van het huidige programma (het “cilinder” -
programma):
Komt de controlesom niet hiermee overeen, dan hebt u het programma niet goed
ingevoerd.
U ziet dat alle toepassingsprogramma’s in de hoofdstukken 16 tot en met 17 bij
iedere routine een controlesom vermelden, zodat u kunt controleren of u ze correct
hebt ingevoerd.
Verder heeft iedere vergelijking in een programma een controlesom. Zie “Een
vergelijking in een programmaregel opnemen” eerder in dit hoofdstuk.
Niet-programmeerbare functies
De volgende functies van de HP 35s zijn niet programmeerbaar:
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
z X
()
/
Toont label C dat 67 bytes
gebruikt.
z
(vasthouden)
/
/
Controlesom en lengte.
{ ()U
{ ()U label regelgetal
az X
Ø, ×,Ö, Õz
{ dG
{Ø, { ×{
z:{ (#º)

Eenvoudig programmeren 13-25
Programmeren met BASE
U kunt instructies programmeren om het talstelsel te veranderen met { w.
Deze instelling werkt in een programma net zo goed als wanneer u hem met het
toetsenbord opgeeft. Daardoor kunt u programma’s schrijven die getallen
accepteren in een talstelsel naar keuze. U kunt rekenen in ieder talstelsel en
resultaten weergeven in ieder talstelsel.
Schrijft u programma’s die een getal gebruiken met een ander grondtal dan 10,
dan moet u het talstelsel opgeven als de huidige instelling van de rekenmachine en
bovendien in het programma (als een instructie).
Een talstelsel kiezen in een programma
Zet de instructie BIN, OCT of HEX aan het begin van het programma. Zet ook een
DEC-instructie aan het einde, zodat de rekenmachine terugkeert naar de decimale
instelling als het programma uitgevoerd is.
Een instructie in een programma om de basismodus te veranderen bepaalt hoe de
invoer geïnterpreteerd wordt en hoe de uitvoer eruit ziet tijdens en na de uitvoering
van het programma, maar heeft geen invloed op de programmaregels zoals u ze
invoert.
Getallen die in programmaregels zijn ingevoerd
Voordat u begint met het programma in te voeren, stel de basismodus in. De
huidige instelling van de basismodus bepaalt het resultaat van het programma.
Een annunciator vertelt u welke basis de huidige instelling is. Vergelijk de
programmaregels hieronder in de decimale en niet-decimale modus. Alle decimale
en niet- decimale getallen staan links in het scherm van de rekenmachine.
Decimaal: Binair:
:
:
:
:
PRGM PRGM BIN
Het decimale
getal kan het teken
“d” weglaten
E Het binaire
getal moet het
basis teken “b”
toevoegen.
:
:
:
:

13-26 Eenvoudig programmeren
Veeltermexpressies en het schema van Horner
Sommige expressies, zoals veeltermen, gebruiken dezelfde variabele meerdere
keren voor de oplossing. Bijvoorbeeld, de expressie
Ax4 + Bx3 + Cx2 + Dx + E
gebruikt de variabele x vier keer. Een programma om een dergelijke expressie te
berekenen met RPN-bewerkingen zou meerdere malen een kopie van x uit een
variabele moeten oproepen.
Voorbeeld:
Schrijf een programma met gebruik van RPN-bewerkingen voor 5x4 + 2x3, dan
evalueer het voor x = 7.
Eenvoudig programmeren 13-27
Evalueer deze veelterm nu voor x = 7.
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
{ d U
!
{ A
z X "! %
5
KX %
0 ¸ºx4
y º 5x4
KX %
0 ¸ºx3
y º 2x3
- 5x4 + 2x3
z !
z X
()
/
Geeft label A, dat 46 bytes
nodig heeft, weer.
z /
/
Controlesom en lengte.
Beëindigt de programma-
invoer.
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
WA%@
waarde
Vraagt om x.
f 8) Resultaat.
13-28 Eenvoudig programmeren
Een meer algemene vorm van dit programma voor een willekeurige vergelijking
Ax4 + Bx3 + Cx2 + Dx + E zou zijn:
"!
"!
"!
"!
"!
"! %
%
º
-
º %
-
º %
-
º %
-
!
Controlesom en lengte: 9E5E 51

Programmeringstechnieken 14-1
14
Programmeringstechnieken
Hoofdstuk 13 behandelde de principes van het programmeren. Dit hoofdstuk
bespreekt wat meer geavanceerde maar handige trucs:
U kunt programma’s vereenvoudigen met subroutines. Een deel van het
programma wordt apart gehouden en van een label voorzien. Zo’n deel
heeft dan een aparte taak. Het gebruik van subroutines maakt een
programma korter in geval een reeks stappen meerdere keren moet worden
uitgevoerd.
Met voorwaardelijke instructies (vergelijkingen en flags) kunt u opgeven
welke instructies als subroutines moeten worden uitgevoerd.
Met lussen en tellers kunt u een groep instructies meerdere malen uitvoeren.
Met indirect adresseren kunt u verschillende variabelen gebruiken met
dezelfde programma-instructie.
Routines in Programma’s
Een programma bestaat uit een of meer routines. Een routine is een functionele
eenheid die een specifieke taak uitvoert. Gecompliceerde programma’s hebben
routines nodig om taken te groeperen en te scheiden. Hierdoor is een programma
makkelijker te schrijven, te lezen, te begrijpen en te onderhouden.
Een routine begint typisch aan een label en eindigt met een instructie dat de
programma/routing uitvoering stopt zoals RTN of STOP.
Subroutines aanroepen (XEQ, RTN)
Een subroutine is een routine die wordt aangeroepen (uitgevoerd) door een andere
routine en die na voltooiing naar diezelfde routine terugkeert.

14-2 Programmeringstechnieken
Als u maar een programma in het geheugen van uw rekenmachine wilt
hebben, kunt u de routine scheiden in diverse labels. Als u meer dan een
programma in het geheugen wilt hebben, is het beter om routines te hebben
die deel zijn van hoofdprogramma label. beginnend met een specifiek
regelgetal.
Subroutine kan zelf andere subroutines aanroepen.
De organigrammen in dit hoofdstuk gebruiken deze notatie:
Het voorbeeld hieronder laat u zien hoe u een subroutine aanroept om het teken
van het getal dat u invoert te veranderen. Subroutine E dat is aangeroepen door
routine D door regel % . Subroutine E eindigt met een RTN instructie
dat de programmauitvoering terugzendt naar routine D (om op te slaan en het
resultaat weer te geven) op regel D004. Zie de organigrammen hieronder.
Geneste subroutines
Een subroutine kan een andere subroutine aanroepen en die subroutine kan weer
een andere subroutine aanroepen. Dit “nesten” van subroutines — een subroutine
aanroepen vanuit een andere subroutine — is beperkt tot een diepte van twintig
niveaus (het bovenste niveau niet meegeteld). De werking van subroutines wordt
hier geïllustreerd:
! 1Uitvoering van het programma vertakt van deze
regel naar het regelgetal dat gemarkeerd is met
1 (“van 1”).
1Uitvoering van het programma vertakt van een
regelgetal die gemarkeerd is met 1 (“naar
1”) naar deze regel.
Uitvoering begint hier.
"! %
% 1Roept subroutine E aan.
! % 2Komt hier terug.
#$ %
!
1Start van subroutine.
-+. Verandert teken van het getal
! 2Terug naar routine D.

Programmeringstechnieken 14-3
HOODFDPROGRAMMA
(Bovenste niveau)
Eind van programma
Probeert u meer dan twintig niveaus diep te gaan, dan krijgt u de foutmelding %
#$.
Voorbeeld: een geneste subroutine.
De volgende subroutine, genaamd S, berekent de waarde van de expressie
als deel van een berekening in een groter programma. De subroutine roept een
andere subroutine aan (een geneste subroutine) met de naam Q, voor het
herhaaldelijk vermenigvuldigen en optellen. Dit bespaart geheugen omdat het
programma zo korter is dan zonder subroutine.
2222 dcba +++

14-4 Programmeringstechnieken
In de RPN-stand,
Vertakken (GTO)
Bij de subroutines zagen we dat het vaak gewenst is de uitvoering te vervolgen met
een andere regel dan de direct daaropvolgende regel. Dit heet vertakken.
Unconditonele vertakking gebruikt de GTO (ga naar) instructie voor het vertakken
van een specifieke programmaregel (label en regelgetal).
De subroutine begint hier.
"! Invoer van A.
"! Invoer van B.
"! Invoer van C.
"! Invoer van D.
Roept gegevens terug.
ºA2.
% 1A2 + B2.
2 % 3A2 + B2 + C2
4 % 5A2 + B2 + C2+ D2
6 º
! Terug naar hoofdroutine.
135 Geneste subroutine
º65¸
º
-Telt x2 op.
246 ! Keert terug naar subroutine S.
2222 DCBA +++

Programmeringstechnieken 14-5
Een geprogrammeerde GTO-instructie
De instructie GTO label (druk op U label regelgetal) verplaatst de uitvoering
van het programma naar de toegewezen programmaregel. Het programma wordt
vervolgd op de nieuwe locatie en gaat nooit meer automatisch terug naar de plaats
van herkomst. GTO wordt dus niet gebruikt voor subroutines.
Als voorbeeld nemen we het programma “Curve fitting” hoofdstuk 16. De instructie
! ' vertakt van een van drie onafhankelijke initialisatieroutines naar LBL Z,
de routine die het gemeenschappelijke startpunt is van de kern van het programma:
GTO gebruiken op het toetsenbord
U kunt U gebruiken om de programmawijzer naar een bepaald label
regelnummer te verplaatsen zonder een programma uit te voeren.
Kan hier beginnen.
.
.
.
! ' 1Springt naar Z001.
Kan hier beginnen.
.
.
.
! ' 1Springt naar Z001.
Kan hier beginnen.
.
.
.
! ' 1Springt naar Z001.
' '1Springt hierheen.
.
.
.

14-6 Programmeringstechnieken
Naar !: U .
Naar een specifiek regelgetal: U labelregelgetal (regelgetal<1000).
Bijvoorbeeld, UA. Bijvoorbeeld, druk op UA
. Het scherm toont nu “! ”.
Als u naar de eerste regel van een label wilt gaan, bijvoorbeeld. A001:
U (druk en houdt vast), het scherm toont nu “! ”.
Voorwaardelijke instructies
Een andere manier om de volgorde van executie te veranderen is met een
voorwaardelijke test, een vergelijking tussen twee getallen die de volgende
instructie van het programma overslaat als niet aan de voorwaarde is voldaan.
Bijvoorbeeld, een voorwaardelijke instructie op regel A005 is º/@ (d.w.z. is x
gelijk aan nul?). Het programma vergelijkt de inhoud van het X-register met nul. Is
dit X-register inderdaad nul, dan gaat het programma verder met de volgende
regel. Bevat het X-register geen nul, dan wordt de volgende regel overgeslagen,
zodat de executie verder gaat met regel A007. Men noemt dit “Doe dat indien
waar.”
Het bovenstaande voorbeeld toont een algemene techniek die wordt gebruikt bij
voorwaardelijke tests: de regel direct na de test, die alleen wordt uitgevoerd als er
aan de voorwaarde is “voldaan”, is een vertakking naar een ander label. Het effect
van de test is dus dat het programma onder bepaalde omstandigheden met een
andere routine verder gaat.
.
.
.
Doe het volgende
indien waar.
º/@ 2Sla volgende over
indien niet waar.
1 !
2
!
.
.
.
1
.
.
.

Programmeringstechnieken 14-7
Er zijn drie categorieën van voorwaardelijke instructies:
Vergelijkingen. Deze vergelijken de registers X en Y, of ze vergelijken het X-
register met nul.
Flags. Deze bekijken de toestand van een flag die is gezet of gewist.
Lustellers. Deze worden voornamelijk in een lus gebruikt die een aantal keren
moet worden uitgevoerd.
Vergelijkingen (x?y, x?0)
Er zijn 12 vergelijkingen beschikbaar voor de programmeur. Drukt u op z l
of { n dan verschijnt er een menu voor een van de twee testcategorieën:
x?y voor tests die x met y vergelijken.
x?0 voor tests die x met 0 vergelijken.
Onthoud dat x refereert aan het getal in het X-register, en y refereert aan het getal
in het Y-register. Deze vergelijken niet de variabelen X en Y. U kunt x?y en x?0
gebruiken om twee getallen te vergelijken, als een van deze geen echt getal is, zal
het als foutmelding # ! terugkeren.
Selecteer de vergelijkingscategorie en druk op de menutoets voor de gewenste
voorwaardelijke instructie.
De testmenu’s
Als u een voorwaardelijke test uitvoert vanaf het toetsenbord, zal de rekenmachine
& of weergeven.
Bijvoorbeeld, als x = 2 en y = 7, doet u de test x<y.
x?yx?0
≠ voor x ≠ y?≠ voor x≠0?
≤ voor x≤y?≤ voor x≤0?
< voor x<y?< voor x<0?
> voor x>y?> voor x>0?
≥ voor x≥y?≥ voor x≥0?
/ voor x=y?/ voor x=0?
14-8 Programmeringstechnieken
Voorbeeld:
Het programma “Normale en inverse verdelingen” in hoofdstuk 16 gebruikt x<y? in
routine T:
Regel T009 berekent de correctie voor Xguess. Regel T013 vergelijkt de absolute
waarde van de berekende correctie met 0,0001. Is de waarde minder dan 0,0001
(“Doe dat indien waar”), dan voert het programma regel T014 uit; is de waarde
gelijk of groter, dan 0,0001 gaat het programma naar regel T015.
Invoer: Weergave:
In de RPN-stand zlÕÕ(<)&
In de ALG-stand ZzlÕÕ(<)&
Programmaregels:
(In de RPN-stand)
Omschrijving
.
.
.
! ªBerekent de correctie voor Xguess.
! !- %Voegt de correctie toe voor een nieuwe Xguess.
!
! )
! º<¸@ Test om te zien of de correctie significant is.
! ! ! Terug naar het begin van de lus als de correctie
significant is. Gaat verder als de correctie niet
significant is.
! %
! #$ %Geeft de berekende waarden van X weer.
.
.
.

Programmeringstechnieken 14-9
Flags
Een flag is een toestandsindicator. Hij is gezet (true) of gewist (false). Het testen van
een flag is ook een voorwaardelijke test die de regel “Doe dat indien waar” volgt:
de uitvoering van het programma gaat verder als de flag gezet is en slaat een regel
over als de flag gewist.
Betekenis van flags
De HP 35s heeft 12 flags, genummerd van 0 tot en met 11. Alle flags kunnen
gezet, gewist en getest worden met het toetsenbord en met een programma-
instructie. De standaardtoestand van de 12 flags is gewist. Met de bewerking van
drie toetsen in aanhangsel B waarmee het geheugen wordt leeggemaakt, wist u
ook alle flags. De flags worden niet beïnvloed door { () Ö
(&) .
Flags 0, 1, 2, 3, en 4 hebben geen bijzondere betekenis. dat wil zeggen dat
u zelf bepaalt wat ze betekenen in uw programma. (Zie het voorbeeld
hieronder.)
Flag 5. Is deze flag gezet, dan wordt een lopend programma onderbroken
als er een overflow optreedt. U ziet dan de melding #$ en £. Een
overflow treedt op als een berekening een groter getal oplevert dan de
rekenmachine aan kan. In dat geval wordt het grootst mogelijke getal als
antwoord ingevuld. Is flag 5 gewist, dan loopt het programma verder, hoewel
er uiteindelijk #$ op het scherm komt als het programma uiteindelijk
stopt.
Flag 6 wordt automatisch door de rekenmachine gezet elke keer als een
overflow van ! voorkomt (hoewel u ook flag 6 zelf kan zetten). Het
heeft geen effect, maar kan getest worden. Afgezien daarvan, wanneer niet-
decimale talstelsels in programma’s worden gebruikt, wordt flag 6 ook gezet
voor ! in programma’s.
Met flags 5 en 6 hebt u controle over de overflowcondities die tijdens de
uitvoering van het programma kunnen optreden. Door flag 5 te zetten stopt
een programma direct na de regel waarop de overflow optrad. Door flag 6
in een programma te testen, kunt u het verloop van een programma
veranderen in het geval er een overflow is opgetreden.
Flags 7, 8 en 9 bepalen de weergave van breuken. Flag 7 kan ook vanaf het
toetsenbord worden gewijzigd. Als de weergave van breuken in en uit wordt
geschakeld met {, dan wordt in feite flag 7 veranderd.

14-10 Programmeringstechnieken
Toestand
van flag
Betekenis van flag
789
Gewist
(standaard)
Weergave van
breuken
uitgeschakeld,
reële getallen
worden als
decimaal getal
weergegeven.
Noemer van breuk
niet groter dan de
waarde in /c.
Breuken worden
zo veel mogelijk
vereenvoudigd.
Gezet Weergave van
breuken
ingeschakeld;
reële getallen
worden als breuk
weergegeven.
Noemer is een
factor van de
waarde in /c.
Breuken worden
niet
vereenvoudigd.
(Alleen als flag 8
gezet is.)
Programmeringstechnieken 14-11
Flag 10 bepaalt hoe een programma vergelijkingen uitvoert:
Is flag 10 gewist (standaard), dan worden vergelijkingen in lopende
programma’s geëvalueerd en komt het resultaat op de stapel.
Is flag 10 gezet, dan worden vergelijkingen in lopende programma’s
weergegeven als berichten, zodat ze zich gedragen als in een VIEW-
statement:
1. Uitvoering van programma stopt.
2. De programmawijzer gaat naar de volgende programmaregel.
3. De vergelijking wordt weergegeven zonder de stapel te beïnvloeden. De
weergave kan verwijderd worden door te drukken op a of . Door
op een willekeurige toets te drukken wordt deze functie uitgevoerd.
4. Als de volgende programmaregel een PSE instructie is, gaat de
uitvoering door na een pauze van 1 seconde.
De toestand van flag 10 wordt alleen gewijzigd door de bewerkingen SF en
CF vanaf het toetsenbord, of door SF en CF in een programma.
Flag 11 bepaalt of er om invoer wordt gevraagd bij het uitvoeren van een
vergelijking in een programma — het heeft geen invloed op het automatisch
vragen om invoer wanneer de vergelijking vanaf het toetsenbord wordt
uitgevoerd:
Is flag 11 gewist (de standaardtoestand), dan geschiedt het evalueren,
SOLVE, en ∫ FN van vergelijkingen in programma’s zonder onderbreking. De
huidige waarde van iedere variabele in de vergelijking wordt automatisch
gebruikt. Prompts van INPUT worden niet beïnvloed.
Is flag 11 gezet, dan wordt bij iedere variabele om een waarde gevraagd als
deze voor het eerst voorkomt in de vergelijking. Dit geschiedt maar een keer
per variabele, ook als de variabele meerdere keren voorkomt in de
vergelijking. Bij het oplossen wordt er niet gevraagd naar de waarde van de
onbekende, bij het integreren niet voor de waarde waarnaar geïntegreerd
wordt. Prompts onderbreken de uitvoering. Door op f te drukken wordt
de uitvoering hervat met de waarde die u invoerde, of met de oorspronkelijke
waarde van de variabele als u niets anders doet dan op f drukken.
Flag 11 wordt automatisch gewist na de evaluatie, na SOLVE, of na ∫ FN van
een vergelijking in een programma. De toestand van flag 11 wordt natuurlijk
ook veranderd door de instructies SF en CF op het toetsenbord en door SF en
CF in een programma.

14-12 Programmeringstechnieken
Annunciators voor gezette flags
De flags 0, 1, 2, 3 en 4 hebben annunciators in het scherm die zichtbaar worden
als een flag gezet is. Aan de aanwezigheid of afwezigheid van de cijfers 0, 1, 2,
3 of 4 kunt u zien of een van deze vijf flags gezet is of niet. Er is geen indicatie
voor flag 5 tot en met 11. De staten van deze flags kunnen worden bepaald met de
instructie FS? van het toetsenbord. (Zie “Flags gebruiken” hieronder.)
Flags gebruiken
Door te drukken op z x verschijnt het menu FLAGS: @
Nadat u de gewenste functie geselecteerd hebt, wordt gevraagd om het nummer
van de flag (0-11). Bijvoorbeeld, druk op z x( ) om flag 0 te
zetten; op z x( ) om flag 10 te zetten; en op z
x( ) om flag 11 te zetten.
Het menu FLAGS
Een flagtest is een voorwaardelijke test die de uitvoering van een programma
beïnvloedt, net als de vergelijkingen. De instructie FS? n controleert of de gegeven
flag gezet is. Zo ja, dan wordt de volgende regel in het programma uitgevoerd. Zo
niet, dan wordt de volgende regel overgeslagen. Dit is de “Doe dat indien waar”-
regel, die we ook al illustreerden onder “Voorwaardelijke instructies” eerder in dit
hoofdstuk.
Test u een flag met het toetsenbord, dan verschijnt op de rekenmachine “& ” of
“”.
Menutoets Omschrijving
nZet flag. Zet flag n.
nWis flag. Wis flag n.
@ n Is flag gezet? Test de toestand van flag n.
Programmeringstechnieken 14-13
Het is een goede gewoonte bij het programmeren om ervoor te zorgen dat alle
voorwaarden die u gebruikt met een bekende aanvangssituatie beginnen. De
huidige waarden van flags zijn afhankelijk van hoe vorige programma’s ze hebben
achtergelaten. U moet niet veronderstellen dat een flag bij het starten van een
programma gewist is, en dat hij alleen maar gezet kan worden als uw eigen
programma daarvoor zorgt. Zorg er dus voor dat de flags gewist worden, voordat
de voorwaarde optreedt waaronder hij gezet zou kunnen worden. Zie het
voorbeeld hieronder.
Voorbeeld: Flags gebruiken.
Als u regels S002 CF0 en S003 CF1 schrijft (zoals hierboven), worden de flags 0
en 1 gewist dus de lijnen S006 en S010 nemen niet de natuurlijke logaritmes van
de X en Y- invoeren.
Als u de regels S002 en S003 van SF 0 en CF 1 vervangt, dan is flag 0 gezet dus
regel S006 neemt dan de natuurlijke log van de X-invoer.
Als u de regels S002 en S003 van CF 0 en SF 1 vervangt, dan is flag 1 gezet dus
regel S010 neemt dan de natuurlijke log van de Y-invoer.
Programmaregels:
(In de RPN-stand)
Omschrijving:
Wist flag 0, de indicator voor In X.
Wist flag 1, de indicator voor In Y.
"! %Vraagt invoer van X
@ Als flag 0 gezet…
… dan wordt de natuurlijke log genomen van de
X-invoer
! %Slaat de waarde in X op na de flag test
"! &Vraagt invoer van Y.
@ Is flag 1 gezet…
… dan wordt de natuurlijke log genomen van de
Y-invoer
! &Slaat de waarde in Y op na de flag test.
#$ %Geeft waarde weer
#$ &Geeft waarde weer
!
Controlesom en lengte: 16B3 42

14-14 Programmeringstechnieken
Als u de regels S002 en S003 van SF0 en SF1 vervangt, dan is flag 0 en 1 gezet
dus regel S006 en S010 neemt dan de natuurlijke log van de X- et Y-invoer.
Gebruik bovenstaand progamma om te zien hoe je flags moet gebruiken
U kunt drie andere gevallen proberen. Onthoud om op z x()
en z x() te drukken om de flag 1 en 0 te wissen nadat u ze
geprobeerd heeft.
Voorbeeld: De weergave van een breuk.
In het volgende programma oefent u met de mogelijkheden van de rekenmachine
om een breuk weer te geven. Het programma vraagt om uw invoer en gebruikt die
voor een gebroken getal en een noemer (de waarde /c). Het programma bevat ook
voorbeelden van het gebruik van de drie flags (7, 8, en 9) voor de weergave van
breuken, en flag (10) voor het “weergeven van berichten”.
Berichten in het programma worden weergegeven als MESSAGE en ingevoerd als
vergelijkingen:
1. Stel de vergelijkingenstand in met G (de annunciator EQN verschijnt).
2. Druk op K letter voor ieder letter in het bericht; druk op {o voor
iedere spatie.
3. Druk op om het bericht in de huidige programmaregel in te voegen en
de vergelijkingenstand te beëindigen.
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
WS%@
waarde
Voert label S uit; vraagt om de X
waarde
f &@
waarde
Slaat 1 op in X; vraagt om de Y
waarde
f %/
)
Slaat 1 op in X; geeft de X
waarde weer na de flag test
f&/
)
Geeft de Y waarde weer na de
flag test

Programmeringstechnieken 14-15
Programmaregels:
(In de RPN-stand)
Omschrijving:
Hier begint het breukenprogramma.
Wist de drie breukflags.
Geeft berichten weer.
Kiest een decimaal grondtal.
"! #Vraagt om een getal.
"! Vraagt om een noemer (2 – 4095).
#Geeft bericht weer, laat daarna decimaal
getal zien.
!
+F Stelt /c in en zet flag 7.
#
! Geeft bericht weer, laat daarna de breuk
zien.
!
Zet flag 8.
! Geeft bericht weer, laat daarna de breuk
zien.
!
Zet flag 9.
% Geeft bericht weer, laat daarna de breuk
zien.
!
! Gaat naar begin van programma.
Controlesom en lengte: BE54 123

14-16 Programmeringstechnieken
Gebruik het bovenstaande programma om de verschillende manieren te zien
waarop een breuk wordt weergegeven:
Lussen
Door terugwaarts te springen — dat wil zeggen naar een label in een eerdere regel
— kunt u een deel van een programma meerdere keren uitvoeren. Dit heet een lus.
"!
"!
"! !
!
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
WF#@
waarde
Voert label F uit; vraagt om een
breuk (V).
f @
waarde
Slaat 2,53 op in V; vraagt om de
noemer (D).
f
)
)
Slaat 16 op in /c. Geeft het bericht
weer gevolgd door een decimaal
getal.
f !
+ d
+
Bericht geeft de wijze aan waarop
de breuk wordt weergegeven
(noemer is niet groter dan 16) en
toont daarna de breuk. d geeft aan
dat de noemer “iets lager” is dan 8.
f!
+ c
+
Bericht geeft de wijze aan waarop
de breuk wordt weergegeven
(noemer is een factor van 16), en
toont daarna de breuk.
f%
+ c
Bericht geeft de wijze waarop de
breuk wordt weergegeven (noemer
is 16), en toont daarna de breuk.
fzx
()
)
)
Stopt het programma en wist flag 10
Programmeringstechnieken 14-17
Deze routine is een voorbeeld van een oneindige lus. Het kan gebruikt worden om
de begingegevens te verzamelen. Nadat de drie waarden zijn ingevoerd, is het
aan u om deze lus handmatig te onderbreken door op het W label regelgetal te
drukken voor het uitvoeren van andere routines.
Voorwaardelijke lussen (GTO)
Wilt u een bewerking uitvoeren, totdat er aan een bepaalde voorwaarde is
voldaan, maar weet u niet hoe lang dat duurt, dan moet u een lus schrijven met een
voorwaardelijke test en een GTO-instructie.
Bijvoorbeeld, de volgende routine gebruikt een lus om de waarde A te verminderen
met een constante waarde B, totdat A kleiner is dan of gelijk aan B.
Programmaregels:
(In de RPN-stand)
Omschrijving:
"!
"!
Het is gemakkelijker A op te roepen dan te onthouden
waar het in de stapel staat.
. Berekent A – B.
! Vervangt de oude A door de nieuwe.
Roept de constante op voor de vergelijking.
º6¸@ Is B < de nieuwe A?
! Ja: herhaal de procedure.
#$ Nee, stop en geef de nieuwe A weer.
!
Controlesom en lengte: 2737 33
14-18 Programmeringstechnieken
Lussen met tellers (DSE, ISG)
Wilt u een lus een aantal keren uitvoeren, gebruik dan de voorwaardelijke functies
z k (verhogen en overslaan indien groter) of { m (verlagen en
overslaan indien kleiner of gelijk). Steeds als een lus in een programma wordt
uitgevoerd, wordt een teller in een variabele automatisch verlaagd of verhoogd. De
huidige teller wordt vergeleken met een eindwaarde, en afhankelijk van het
resultaat van de vergelijking wordt de lus voortgezet of beëindigd.
Om omlaag te tellen, gebruikt u { m variabele
Om omhoog te tellen, gebruikt u z k variabele
Deze functies doen hetzelfde als een FOR–NEXT-lus in BASIC:
variabele = beginwaarde ! eindwaarde ! stap
.
.
.
%! variabele
Een DSE-instructie is als een FOR–NEXT-lus met een negatieve stap.
Nadat u een shifttoets indrukt voor ISG of DSE (z k of { m), wordt er
gevraagd naar de variabele waarin de lusteller zich bevindt (zie hieronder).
De lusteller
De opgegeven variabele moet een lusteller bevatten, ±ccccccc.fffii, waarin:
±ccccccc de huidige waarde van de teller is (1 à 12 cijfers). Deze waarde
verandert steeds terwijl de lus wordt uitgevoerd.
fff is de uiteindelijke waarde van de teller (altijd drie cijfers). Deze waarde
verandert niet terwijl de lus wordt uitgevoerd. Een ongespecificeerde waarde
voor fff wordt verondersteld 000 te zijn.

Programmeringstechnieken 14-19
ii is de waarde waarmee de teller verhoogd of verlaagd moet worden (dit
moeten twee cijfers zijn). Deze waarde verandert niet. Ontbreekt deze
waarde voor ii, dan wordt hij verondersteld 01 te zijn, dus dan wordt er
verhoogd of verlaagd met 1.
Bij het uitvoeren van de lusinstructie handelt DSE als volgt. De lusteller is
ccccccc.fffii. DSE berekent ccccccc = ccccccc — ii, vergelijkt de nieuwe ccccccc
met fff en slaat de volgende programmaregel over als ccccccc ≤ fff.
En ISG handelt als volgt. De lusteller is ccccccc.fffii. ISG berekent ccccccc = ccccccc
+ ii, vergelijkt de nieuwe ccccccc met fff en slaat de volgende programmaregel over
als ccccccc > fff.
Bijvoorbeeld, de lusteller 0,050 betekent voor ISG dat er wordt begonnen met nul,
dat die waarde steeds met 1 verhoogd moet worden tot de waarde 50 is bereikt.
Als de lusteller een complex getal of een vector is, zal het het echte deel of eerste
deel nemen om de lus te controleren.
Het volgende programma gebruikt ISG om een lus 10 keer uit te voeren in RPN
modus. De lusteller (1,010) bevindt zich in variabele Z. Nullen aan het begin en het
einde mogen worden weggelaten.
Is huidige waarde
> eindwaarde, ga
dan verder met de
lus.
1
1
$ $
.
.
.
$
$ ! $
$ % %
.
.
.
2
2
Is huidige
waarde ≤
eindwaarde,
beëindig dan de
lus.
Is huidige waarde
≤ eindwaarde, ga
dan verder met de
lus.
1
1
$ $
.
.
.
$
$ ! $
$ % %
.
.
.
2
2
Is huidige
waarde >
eindwaarde,
beëindig dan de
lus.

14-20 Programmeringstechnieken
)
! '
'
!
!
Druk op WL, druk dan op z Z om te zien dat het
lusteller nu 11,0100 is.
Variabelen en labels indirect adresseren
Indirect adresseren is een techniek die door geavanceerde programmeurs wordt
gebruikt om een variabele of label te gebruiken zonder tevoren op te geven welke
variabele dat is. Dit wordt bepaald als het programma draait, het is dus afhankelijk
van de tussenresultaten (of invoer) van het programma.
Indirect adresseren werkt met vier verschillende toetsen: 0, 7, 1 , en A.
Deze toetsen zijn voor vele functies aktief dat A neemt door Z als variabelen of
labels.
I en J zijn variabelen waarvan de inhoud kan verwijzen naar een andere
variabele. Deze bevat een waarde zoals iedere andere (A tot en met Z).
(I) en (J) zijn programmeerfuncties die aangeven, “Gebruik het getal in I of J
om te bepalen welke variabele of label geaddresseerd moet worden.”
Dit is een indirect adres. (A tot en met Z zijn directe adressen.)
Zowel 0 en 7 worden samen gebruikt voor het creëren van een indirect adres
en dit geldt ook voor 1 en A.
Op zich is (I) of (J) ongedefinieerd (geen waarde in (I) of (J)) of onbestuurd (maakt
gebruik van het getal dat zich toevallig nog in I of J bevindt.
De variabele “I” en “J”
U kunt de inhouden van I of J opslaan, oproepen en manipuleren zoals u dat kunt
doen met de inhouden van andere variabelen. U kunt zelfs voor I, J oplossen en
intergreren met gebruik van I of J. De onderstaande functies kunnen de variabele “i”
gebruiken. ( de variabele J is hetzelfde).
Programmeringstechnieken 14-21
Het indirecte adres, (I) en (J)
Veel functies die gebruik maken van A tot en met Z (als variabelen of labels) kunnen
(I) of (J) gebruiken om indirect te verwijzen naar A tot en met Z (variabelen of
labels) of naar statistische registers. De functie (I) of (J) gebruikt de waarde van de
variabele I à J om te bepalen welke variabele, welk label, of welk register
geadresseerd moet worden. De volgende tabel laat zien hoe.
STO I INPUT I DSE I
RCL I VIEW I ISG I
STO +,–, × ,÷ I ∫ FN d I x < > I
RCL +,–, × ,÷ ISOLVE I

14-22 Programmeringstechnieken
De bewerkingen INPUT(I) ,INPUT(J) en VIEW(I) ,VIEW(J) zetten de naam van de
indirect geadresseerde variabele of het indirect geadresseerde register.
Met het menu SUMS kunt u waarden oproepen uit de statistische registers. U moet
echter indirecte adressering gebruiken voor andere bewerkingen met deze
registers, zoals STO, VIEW en INPUT.
De hieronder genoemde functies kunnen (I) of (J) als adres gebruiken. Voor FN=
verwijst (I) of (J) naar een label; voor alle andere functies verwijst (I) of (J) naar
een variabele of register.
Bevat I/J: Dan adresseert (I)/(J):
-1 variabele A of label A
.
.
.
.
.
.
-26 variabele Z of label Z
-27 n register
-28 Σx register
-29 Σy register
-30 Σx2 register
-31 Σy2 register
-32 Σxy register
0 Naamloze Indirecte variabelen
start
.
.
.
.
.
.
800 Het Maximale Adres is 800
I<-32 of I>800 of variabelen
ongedefinieerd fout: # 12
J<-32 of I>800 of variabelen
ongedefinieerd fout: # 12
Programmeringstechnieken 14-23
U kunt geen naamloze variabelen of statische register oplossen of integreren.
Programmabesturing met (I)/(J)
Aangezien de inhoud van I elke keer kan veranderen als het programma bezig is
— of zelfs in verschillende delen van hetzelfde programma — een programma
instructie zoals STO (I) of (J) kan waarde opslaan in een andere variabele op
verschillende momenten. Bijvoorbeeld, STO (-1) geeft de opslag van de waarde in
Variabele A aan. Dit handhaaft de flexibiliteit door het precies (als het programma
werkzaam is) open te laten welke variabele of programmalabel nodig zal zijn.
Indirect adresseren is zeer bruikbaar bij het tellen en besturen van lussen. De
variabele I of J dient dan als index, met het adres van de variabele die de lusteller
bevat voor de functies DSE en ISG.
Vergelijkingen met (I)/(J)
U kunt (I) of (J) in een vergelijking gebruiken om een variabele indirect aan te
geven. Let op dat 12 of 12 betekent dat de variabele is aangegeven door het
getal in variabele I or J (een indirecte referentie), maar dat I of J en 12of 12 (
waar de haakjes van de gebruiker worden gebruikt in plaats van de (I) of (J) toets),
betekent variabele I of J.
Naamloze indirecte variabelen
Het plaatsen van een positief getal in variabele I of J geeft u toegang tot maximaal
801 indirecte variabelen. Het volgende voorbeeld geeft aan hoe ze te gebruiken.
STO(I)/(J)
RCL(I)/(J)
STO +, –,× ,÷, (I)/(J)
RCL +, –,× ,÷, (I)/(J)
X<>(I)/(J)
FN=(I)/(J)
INPUT(I)/(J)
VIEW(I)/(J)
DSE(I)/(J)
ISG(I)/(J)
SOLVE(I)/(J)
∫ FN d(I)/(J)
14-24 Programmeringstechnieken
Opmerking:
1. Als u de waarde van een ongedefinieerd opslagadres wilt oproepen, zal de
foutmelding “# 12” te zien zijn . (Zie A014)
2. De rekenmachine verplaatst geheugen voor variabele 0 in de laatste niet- nul
variabele. Het is belangrijk om 0 op te slaan in variabelen na gebruik om het
geheugen te legen. Elk verplaatste indirecte register gebruikt 37 bytes aan
programmageheugen.
3. Er is een maximum van 800 variabelen.
Programmaregels:
(In de RPN-stand)
Omschrijving:
!
! 12 Definieert het opslagen adresbereik “0-100” en
bewaart “12345” in adres 100.
!
! 12 Bewaart “67890” in adres 150. Het gedefinieerde
indirecte opslagbereik is nu “0-150”.
!
! 12 Slaat 0 in het indirecte register 100 op. Het
gedefinieerde bereik is nog steeds “0-150”.
!
12 Toont “INVALID (I)”, omdat adres “170” niet
gedefinieerd is.
!

Programma’s oplossen en integreren 15-1
15
Programma’s oplossen en integreren
Een Programma oplossen
In hoofdstuk 7 zagen we hoe u een vergelijking kunt invoeren — hij wordt
toegevoegd aan de vergelijkingenlijst — en voor een willekeurige variabele kunt
oplossen. U kunt ook een programma invoeren dat een functie berekent en dat voor
een willekeurige variabele oplost. Dat is vooral handig als de vergelijking voor
verschillende condities anders is, of als er herhaalde berekeningen moeten worden
uitgevoerd.
Een geprogrammeerde functie oplossen:
1. Voer een programma in dat de functie definieert. (Zie hieronder “Een
programma schrijven voor SOLVE”.)
2. Selecteer het programma dat u wilt oplossen: druk op z V label. (Deze
stap kunt u overslaan als u hetzelfde programma opnieuw gebruikt.)
3. Los op voor de onbekende variabele: druk op { variable.
U ziet dat FN= vereist is als u een geprogrammeerde functie oplost, maar niet als u
een vergelijking oplost in de vergelijkingenlijst.
Om een berekening af te breken, druk op of fen het bericht
!"! verschijnt in regel 2. De huidige beste berekening van de wortel
bevindt zich in de onbekende variabele.; gebruik z om het te bekijken
zonder de stapel te verstoren. Om door te gaan met de berekening, druk op f.
Een programma schrijven voor SOLVE:
Het programma kan gebruik maken van vergelijkingen, ALG, RPN — U kiest zelf in
welke combinatie.
15-2 Programma’s oplossen en integreren
1. Begin het programma met een label. Dit label identificeert de functie die met
SOLVE geëvalueerd moet worden (/label).
2. Schrijf een INPUT-instructie voor iedere variabele, inclusief de onbekende.
INPUT-instructies maken het mogelijk dat u voor iedere variabele in een functie
met meerdere variabelen oplost. INPUT voor de onbekende wordt door de
rekenmachine genegeerd, dus u hoeft maar één programma te schrijven met
een aparte INPUT-instructie voor iedere variabele (inclusief de onbekende).
Als u geen INPUT instructies schrijft, zal het programma de waarden gebruiken
die zijn opgeslagen in de variabelen of ingevoerd op vergelijkingen prompts.
3. Voer de instructies in om de functie te evalueren.
Een functie die geprogrammeerd is als een functie die geprogrammeerd is
als een RPN- of ALG-reeks van meerdere regels moet uiteindelijk nul
geven. Is de vergelijking f(x) = g(x), dan berekent uw programma f(x) –
g(x). “=0” wordt verondersteld.
Een functie die geprogrammeerd is als een vergelijking kan van ieder type
zijn — gelijkheid, toekenning of expressie. De vergelijking wordt door het
programma geëvalueerd en de waarde moet nul zijn. Wilt u dat de
vergelijking vraagt om de waarden van variabelen, zonder INPUT-
instructies te gebruiken, dan moet flag 11 gezet zijn.
4. Beëindig het programma met een RTN. De uitvoering moet eindigen met de
waarde van de functie in het X-register.
Voorbeeld: Een programma met ALG.
Schrijf een programma met ALG-bewerkingen dat een willekeurige onbekende
oplost in de wet van “Boyle-Gay Lussac”. De vergelijking is:
P x V= N x R x T
waarin
P = Druk (atmosfeer of N/m2).
V = Inhoud (liters).
N = Hoeveelheid gas (mol)
R = De universele gasconstante
(0,0821 liter-atm/mol-K of 8,314 J/mol-K).
T = Temperatuur (Kelvin; K = °C + 273,1).
Programma’s oplossen en integreren 15-3
Zet allereerst de rekenmachine in de programmeerstand; zet zonodig de
programmawijzer bovenaan het programmageheugen.
Voer het programma in:
Druk op om de programmainvoer te beëindigen.
Gebruik programma “G” om op te lossen voor 0,005 mol kooldioxide in een vat
van 2 liter bij 24°C.
Invoer:
(In de ALG-stand)
Weergave: Omschrijving:
{ d
U !
Programmeerstand.
Programmaregels:
(In de ALG-stand)
Omschrijving:
Identificeert de geprogrammeerde functie.
"! Slaat P op voor druk
"! #Slaat V op voor volume
"! Slaat N op voor de hoeveelheid gas
"! Slaat R op voor de gasconstante
"! !Slaat T op voor temperatuur
×#/××!Druk op G
Druk × volume = Mol × gasconstante × temp.
! Beëindigt het programma.
Controlesom en lengte: F425 33
Invoer:
(In de ALG-stand)
Weergave: Omschrijving:
zVGSelecteert “G” — het programma.
SOLVE evalueert om de waarde
van de onbekende te vinden.
{P#@
waarde
Selecteert P; vraagt om V.
f @
waarde
Slaat 2 op in V; vraagt om N.
15-4 Programma’s oplossen en integreren
Voorbeeld: Programma dat een vergelijking gebruikt.
Schrijft een programma dat een vergelijking gebruikt om de wet van “Boyle-Gay
Lussac” op te lossen.
Bereken nu de druk van het kooldioxide als de temperatuur 10°C lager is dan in het
vorige voorbeeld.
f @
waarde
Slaat ,005 op in N; vraagt om R.
f
!@
waarde
Slaat ,0821 op in R; vraagt om T.
!@
)
Berekent T.
f #
/
)
Slaat 297,1 op in T; lost P op. De
druk is 0,0610 atm.
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
{ d
U !
Naar de programmeerstand.
Programmawijzer bovenaan de
lijst van programma’s.
{ H Geeft het programma een label.
z x
(1 )
Zet de prompts in de vergelijking
aan.
G
KP y
KV z c
KN y
KR y
KT º#/ºº!
Evalueert de vergelijking, flag 11
wordt gewist. (Controlesom en
lengte: EDC8 9).
z ! Beëindigt het programma.
) Beëindigt de programmeerstand.
Controlesom en lengte van het programma: DF52 21
Programma’s oplossen en integreren 15-5
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
{HL) Slaat vorige druk op.
z VH) Selecteert programma “H.”
{P#@
)
Selecteert variabele P; vraagt om V.
f@
)
Bewaart 2 in V; vraagt om N.
f@
)
Bewaart ,005 in N; vraagt om R.
f!@
)
Bewaart ,0821 in R; vraagt om T.
!@
)
Berekent nieuwe T.
f #
/
)
Slaat 287,1 op in T; lost op voor
nieuwe P.
KL.) Berekent de drukverandering als de
temperatuur van het gas daalt van
297,1 K naar 287,1 K (een negatief
resultaat duidt op een lagere druk).

15-6 Programma’s oplossen en integreren
SOLVE in een programma gebruiken
U kunt SOLVE gebruiken als deel van een programma.
Desgewenst kunt u de beginwaarden opgeven (in de onbekende variabele en het X-
register), voordat u de instructie SOLVE variabele start. De twee instructies voor het
oplossen van een vergelijking voor een onbekende variabele verschijnen in een
programma als:
/ label
# variabele
De geprogrammeerde SOLVE-instructie geeft geen weergave met een label
(variabele = waarde), omdat dat voor uw programma wellicht geen significante
uitvoer is (dat wil zeggen, u wilt misschien andere berekeningen uitvoeren voor u
het getal weergeeft). Wilt u het resultaat wel weergeven, voeg dan de instructie
VIEW variabele toe na de SOLVE-instructie.
Wordt er geen oplossing gevonden voor de onbekende variabele, dan slaat u de
volgende programmaregel over (volgens de regel “Doe dat indien waar”, die is
uitgelegd in hoofdstuk 14). Het programma moet dan de situatie opvangen waarin
er geen wortel is gevonden, bijvoorbeeld door het met andere beginwaarden te
proberen of door een invoerwaarde te veranderen.
Voorbeeld: SOLVE in een Programma.
Het volgende uittreksel komt uit een programma waarmee u x of y kunt oplossen
door te drukken op W X of Y.

Programma’s oplossen en integreren 15-7
Integreren met een programma
In hoofdstuk 8 zagen we hoe we een vergelijking (of expressie) invoerden — deze
wordt toegevoegd aan de lijst van vergelijkingen — en integreerden naar een
bepaalde variabele. U kunt ook een programma schrijven dat een functie berekent
en naar een bepaalde variabele integreert. Dat is vooral handig als de functie
onder bepaalde voorwaarden verandert of als er herhaalde berekeningen in
voorkomen.
Een geprogrammeerde functie integreren:
1. Voer een programma in dat de functie van de integrand definieert. (Zie “Een
programma schrijven voor ∫ FN” hieronder.)
Programmaregels:
(In de RPN-stand)
Omschrijving:
% %Instelling voor X.
% Index voor X.
% ! Naar hoofdroutine.
Controlesom en lengte: 62A0 11
& &Instelling voor Y.
& Index voor Y.
& ! Naar hoofdroutine.
Controlesom en lengte: 221E 11
Hoofdroutine.
! Slaat index op in I
/ Definieert op te lossen programma.
#12Lost op voor een gegevens variabele.
#$12Geeft de oplossing weer.
! Beëindigt het programma.
Controlesom en lengte: D45B 18
)
)
)
Berekent f (x,y). De vergelijking en INPUT
vragen om de vereiste waarden.
!
15-8 Programma’s oplossen en integreren
2. Selecteer het programma dat de te integreren functie definieert: druk op z
V label. (U kunt deze stap overslaan als u hetzelfde programma weer
integreert.)
3. Voer de grenzen van de integratie in: toets in de onder grens en druk op
, toets dan de bovenste grens in.
4. Selecteer de variabele waarnaar geïntegreerd moet worden en start de
berekening: druk op z ) variabele.
U ziet dat FN= vereist is als u een geprogrammeerde functie integreert, maar niet
als u een vergelijking integreert uit de vergelijkingenlijst.
U kunt een werkende integratieberekening afbreken door het drukken op of
f en het bericht !"! verschijnt in regel 2. Maar, de berekening
kan niet worden voortgezet. Geen informatie over de integratie is beschikbaar
totdat de berekening normaal is beëindigd.
Drukken op Wterwijle een integratieberekening bezig is, zal de )V
bewerking doen stoppen. In dit geval, moet u )V van voren af aan weer
laten beginnen.
Een programma schrijven voor ∫ FN:
Het programma vergelijkingen, ALG- en RPN-bewerkingen gebruiken — in de
combinatie die u zelf verkiest.
1. Begin het programma met een label. Dit label identificeert de functie die u wilt
integreren (/label).
2. Schrijf een INPUT-instructie voor iedere variabele, ook voor de variabele
waarnaar geïntegreerd wordt. INPUT-instructies maken het mogelijk naar
iedere gewenste variabele te integreren in een functie met meerdere
variabelen. INPUT voor de variabele waarnaar geïntegreerd wordt, wordt
genegeerd door de rekenmachine, zodat u maar één programma hoeft te
schrijven met aparte separate INPUT-instructies voor iedere variabele (inclusief
de variabele waarnaar geïntegreerd wordt).
Als u geen INPUT instructies schrijft, gebruikt het programma de opgeslagen
waarden in de variabelen of die ingevoerd zijn als vergelijkingsprompts.
3. Voer de instructies in om de functie te evalueren.

Programma’s oplossen en integreren 15-9
Een functie die geprogrammeerd is als een reeks ALG - en RPN-instructies
moet de functiewaarden berekenen die u wilt integreren.
Een functie die geprogrammeerd is als een vergelijking is meestal een
expressie met de integrand — maar het kan ook een vergelijking zijn van
een ander type. Wilt u dat de vergelijking vraagt om de waarden van
variabelen, zonder INPUT-instructies op te geven, zet dan flag 11.
4. Beëindig het programma met een RTN. De uitvoering moet eindigen met de
waarde van de functie in het X-register.
Voorbeeld: Programma dat een vergelijking gebruikt.
De sinusintegraal van het voorbeeld in hoofdstuk 8 is
Deze functie kan geëvalueerd worden door een programma te integreren dat de
integrand definieert:
Voer dit programma in en integreer de sinusintegraalfunctie naar x van 0 tot 2 (t =
2).
Definieert de functie.
1%2ª%De functie als expressie. (Controlesom en lengte: 0EE0
8).
! Sluit de subroutine af
Controlesom en lengte van het programma: D57E 17
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
9 (2) Selecteert radialen.
z VSSelecteert label S als integrand.
_Geeft de integratiegrenzen op.
z )X!!
∫ /
)
Integreert de functie van 0 tot 2;
geeft het resultaat weer.
9 (1)) Herstelt de Graden.
∫
=t
0 dx( Si(t) )
x
xsin

15-10 Programma’s oplossen en integreren
Integratie in een programma
Integratie kan vanuit ieder programma gestart worden. Denk eraan dat u de
integratiegrenzen opgeeft voordat u de integratie uitvoert, en houd er rekening mee
dat de nauwkeurigheid van het resultaat afhankelijk is van de nauwkeurigheid van
de schermweergave op het moment dat het programma draait. De twee integratie-
instructies verschijnen in het programma als:
/ label
∫ G variabele
De geprogrammeerde ∫ FN-instructie geeft geen waarde weer met een label (∫ =
waarde), omdat dit misschien niet de significante uitvoer is van uw programma (dat
wil zeggen, u wilt misschien nog verdere berekeningen met het getal uitvoeren
voordat u het weergeeft). Wilt u het resultaat weergeven, schrijf dan een PSE-( {
e ) of STOP-(f) instructie om het resultaat in het X-register na de ∫ FN-
instructie weer te geven.
Als de PSE instructie onmiddelijk een weergegeven vergelijking volgt (Flag 10
gezet) telkens elke herhaling van integratie of oplossing, zal de vergelijking worden
getoond voor 1 seconde en de uitvoering zal doorgaan tot het einde van elke
herhaling. Tijdens de weergave van de vergelijking, is scrollen of toetsenbord
gebruik niet mogelijk.
Voorbeeld: ∫ FN in een programma.
Het programma “Normale en inverse verdelingen” in hoofdstuk 16 bevat een
integratie van de vergelijking van de functie van normale dichtheid
De functie is berekend met de routine F. Andere routines vragen voor
de bekende waarden en doen de andere berekeningen voor het vinden van Q(D),
het bovenstaartgedeelte van een normale curve. De integratie zelf is gezet en
uitgevoerd vanuit routine Q:
.e
2
)(
dD
2S
12/
S
MD
D
M
−
−
∫
π
2))(( 2÷÷− SMD
e

Programma’s oplossen en integreren 15-11
Beperkingen bij het oplossen en integreren
De SOLVE variabele en ∫ FN d variabele instructies kunnen niet een routine roepen
dat een andere SOLVE of ∫ FN instructie bevat. Dat wil zeggen, geen van deze
instructies kan recursief gebruikt worden. Bijvoorbeeld, het berekenen van een
multiple integraal heeft als resultaat een ∫ 1∫ 2 fout. En ook, SOLVE en ∫ FN
kunnen geen routine roepen dat een /label instructie bevat; pogingen hiertoe
resulteren in een # !# of ∫ !# foutmelding. SOLVE kan geen
routine roepen dat een ∫ FN instructie bevat (maakt een #1∫ 2 fout), net
zoals ∫ FN geen routine kan roepen dat een SOLVE instructie bevat (maakt een
∫ 1 #2 fout).
De SOLVE variabele en ∫ FN d variabele instructies in een programma gebruiken
een van de 20 hangende subroutines die terugkeren in de rekenmachine (Refereer
aan “Geneste Subroutines“ in hoofdstuk 14.)
%
/
∫ G
Roept de ondergrens van de integratie op.
Roept de bovengrens van de integratie op. (X = D.)
Specificeert de functie.
Integreert de normale functie met de dummy-variabele D.

Statistische programma’s 16-1
16
Statistische programma’s
Curve fitting
Dit programma wordt gebruikt voor een van vier modellen van vergelijkingen van
uw gegevens. Deze modellen zijn: de rechte lijn, de logarithmische curve, de
exponentiële curve en de machtcurve. Het programma accepteert twee of meer (x,
y) paren van gegevens en berekent de correlatiecoëfficiënt, r, en de twee
regressiecoëfficiënten, m en b. Het programma bevat een routine om de schattingen
en te berekenen. (Voor een definitie van deze waarden, zie “Lineaire
regressie” in hoofdstuk 12.)
Voorbeelden van de curves en de relevante vergelijkingen ziet u hieronder. De
interne regressiefuncties van de HP 35s worden gebruikt om de
regressiecoëfficiënten te berekenen.
x
ˆy
ˆ
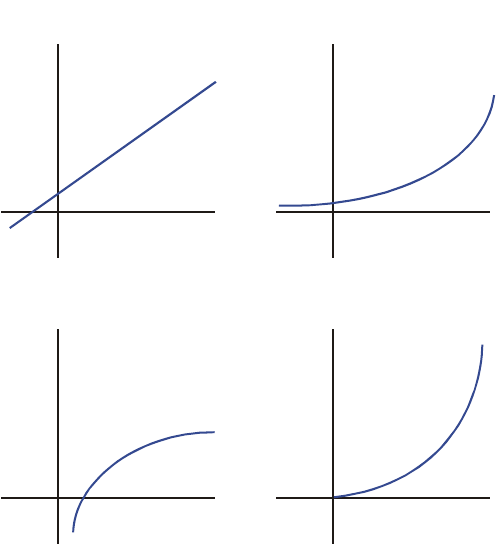
16-2 Statistische programma’s
Voor logaritmische curves, moet x positieve waarden hebben. Voor exponentiële
curves moet de waarde van y positief zijn. Voor machtcurves, moeten zowel x als y
positief zijn. De fout 12 treedt op als u in deze gevallen een negatief
getal opgeeft.
Zeer grote waarden die slechts weinig verschillen kunnen precisieproblemen
opleveren, evenals gegevens die veel in grootte verschillen. Zie “Beperkingen van
de nauwkeurigheid van de gegevens” in hoofdstuk 12.
y
x
y B Mx=+
Straight Line Fit
S
y
x
y Be
Mx
=
Exponential Curve Fit
E
y
x
y B MIn x=+
Logarithmic Curve Fit
L
y
x
y BxM
=
Power Curve Fit
P
Machtcurve M
Logaritmische curve L
Rec
h
te
l
ijn R Exponentië
l
e curve E

Statistische programma’s 16-3
Programmalisting:
Programmaregels:
(In de RPN-stand)
Omschrijving
Deze routine stelt de toestand in voor de rechte lijn.
Wist flag 0, de indicator voor ln X.
Wist flag 1, de indicator voor ln Y.
! ' Gaat naar het gemeenschappelijke startpunt Z.
Controlesom en lengte: 8E85 12
Deze routine stelt de toestand in voor het logaritmische
model.
Zet flag 0, de indicator voor ln X.
Wist flag 1, de indicator voor ln Y
! ' Gaat naar het gemeenschappelijke startpunt Z.
Controlesom en lengte: AD1B 12
Deze routine stelt de toestand in voor het exponentiële
model.
Wist flag 0, de indicator voor ln X.
Zet flag 1, de indicator voor ln Y.
! ' Gaat naar het gemeenschappelijke startpunt Z.
Controlesom en lengte: D6F1 12
Deze routine stelt de toestand in voor het machtmodel.
Zet flag 0, de indicator voor ln X.
Zet flag 1, de indicator voor ln Y.
Controlesom en lengte: 3800 9
' 'Het gemeenschappelijke startpunt voor alle modellen.
' ´Maakt de statistische registers leeg. Druk op
{(4Σ)
' Maakt de lusteller nul voor de eerste invoer.
Controlesom en lengte: 8611 10
$ $Het begin van de invoerlus.
$ Stelt de lusteller in voor de invoer.
$ -
$ ! %Slaat de lusteller op in X zodat hij verschijnt als er om X
wordt gevraagd.
16-6 Statistische programma’s
Controlesom en lengte: 889C 18
Deze subroutine berekent voor het logaritmische model.
&
.
ª
H%Berekent = e(Y – B) ÷ M
! Terug naar oproepende routine.
Controlesom en lengte: 0DBE 18
Deze subroutine berekent voor het exponentiële model.
º %
H%
º Berekent = BeMX.
! Springt naar M005
Controlesom en lengte: 9327 18
Deze subroutine berekent voor het exponentiële model.
&
ª
ª Berekent = (ln (Y ÷ B)) ÷ M.
! Gaat naar N005
Controlesom en lengte: 7219 18
Deze subroutine berekent voor het logaritmische model.
%
¸%
º Berekent Y= B (XM).
! Gaat naar K005
Controlesom en lengte: 11B3 18
Deze subroutine berekent voor het logaritmische model.
Programmaregels:
(In de RPN-stand)
Omschrijving
x
ˆ
x
ˆ
y
ˆ
y
ˆ
x
ˆ
x
ˆ
y
ˆ
x
ˆ
Statistische programma’s 16-7
&
ª
+º
¸%Berekent = (Y/B ) 1/M
! Gaat naar O005
Controlesom en lengte: 8524 21
Bepaald of D001 of B001 zou moeten starten
@ Is flag 1 gezet . . .
% Voert D001 uit
% Voert B001 uit
! & Gaat naar Y006
Controlesom en lengte: 4BFA 15
Bepaald of C001 of A001 zou moeten starten
@ Is flag 1 gezet . . .
% Voert C001 uit
% Voert A001 uit
! & Gaat naar Y006
Controlesom en lengte: 1C4D 15
Bepaald of J001 of H001 zou moeten starten
@ Is flag 1 gezet . . .
% Voert J001 uit
% Voert H001 uit
! & Gaat naar Y011
Controlesom en lengte: 0AA5 15
Bepaald of I001 of G001 zou moeten starten
@ Is flag 1 gezet . . .
% Voert I001 uit
% Voert G001 uit
! & Gaat naar Y011
Controlesom en lengte: 666D 15
Programmaregels:
(In de RPN-stand)
Omschrijving
x
ˆ
16-8 Statistische programma’s
Gebruikte flags:
Flag 0 wordt gezet als een natuurlijke log moet geworden berekend van de X -
invoer. Flag 1 wordt gezet als een natuurlijke log moet geworden berekend van de
Y -invoer.
Als flag 1 is gezet in routine N, is I001 uitgevoerd. Als flag 1 leeg is, G001 is dan
uitgevoerd.
Programma Instructies:
1. Voer de programmaroutines in; druk op als u klaar bent.
2. Druk op W en selecteer het type curve dat u wilt maken:
S voor een rechte lijn;
L voor een a logaritmische curve;
E voor een exponentiële curve; of
P voor een machtcurve.
3. Geef een x–waarde in en druk op f.
4. Geef een y–waarde in en druk op f.
5. Herhaal de stappen 3 en 4 voor ieder gegevenspaar. Ontdekt u dat u een fout
hebt gemaakt, nadat u in stap 3 op f hebt gedrukt (met &@waarde nog
steeds zichtbaar), druk dan weer op f (waarbij de prompt %@waarde
verschijnt) en druk op WU om het laatste paar weer te
verwijderen. Ontdekt u dat u een fout hebt gemaakt na stap 4, druk dan op
WU. In beide gevallen gaat u verder met stap 3.
6. Druk na het invoeren van alle gegevens op WR om de
correlatiecoëfficiënt, R, te zien.
7. Druk op f om de regressiecoëfficiënt B te zien.
8. Druk op f om de regressiecoëfficiënt M te zien.
9. Druk op f voor de prompt %@waarde voor de schattingsroutine van , .
10. Wilt u schatten, uitgaande van x, geef dan x op bij de prompt %@waarde
en druk op f voor (&@).
11. Wilt u schatten, uitgaande van y, druk dan op f tot u de prompt
&@waarde ziet, geef y op, en druk op f voor (%@).
12. Voor meer schattingen gaat u naar stap 10 of 11.
x
ˆy
ˆ
y
ˆ
y
ˆ
x
ˆ
x
ˆ
Statistische programma’s 16-9
13. Voor een nieuw probleem gaat u naar stap 2.
Gebruikte variabelen:
Voorbeeld 1:
Trek een rechte lijn door de gegevens hieronder. Maak een opzettelijke fout in het
derde gegevenspaar en verbeter deze. Schat y voor een x waarde van 37. Schat x
voor een y waarde van 101.
BRegressiecoëfficiënt (y–intercept van een rechte lijn); ook
gebruikt voor tijdelijke opslag.
MRegressiecoëfficiënt (helling van een rechte lijn).
RCorrelatiecoëfficiënt; ook gebruikt voor tijdelijke opslag.
XDe x–waarde van een gegevenspaar bij de invoer, de
hypothetische x bij het projecteren van ; of (x–
schatting) bij een gegeven hypothetische y.
YDe y–waarde van een gegevenspaar bij de invoer, de
hypothetische y bij het projecteren van ; of (y–
schatting) bij een gegeven hypothetische x.
Statistische registers Statistische accumulatie en berekening.
X 40,5 38,6 37,9 36,2 35,1 34,6
Y 104,5 102 100 97,5 95,5 94
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
WS%@
)
Start de rechte-lijnroutine.
f &@
waarde
Geeft x–waarde van gegevenspaar
op.
y
ˆx
ˆ
x
ˆy
ˆ
16-10 Statistische programma’s
Geef nu 379 op in plaats van 37,9, zodat u kunt zien hoe u fouten kunt verbeteren.
f
%@
)
Geeft y–waarde van gegevenspaar
op.
f &@
)
Geeft x–waarde van gegevenspaar
op.
f %@
)
Geeft y–waarde van gegevenspaar
op.
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
f &@
)
Geeft verkeerde x-waarde van
gegevenspaar op.
f%@
)
Haal de prompt %@ terug.
WU%@
)
Verwijdert het laatste paar. Ga nu
verder met de juiste gegevens.
f &@
)
Geeft correcte x-waarde van
gegevenspaar op.
f %@
)
Geeft y–waarde van gegevenspaar
op.
f &@
)
Geeft x–waarde van gegevenspaar
op.
f %@
)
Geeft y–waarde van gegevenspaar
op.
f &@
)
Geeft x–waarde van gegevenspaar
op.
f %@
)
Geeft y–waarde van gegevenspaar
op.
f &@
)
Geeft x–waarde van gegevenspaar
op.
f %@
)
Geeft y–waarde van gegevenspaar
op.
WR/
)
Berekent de correlatiecoëfficiënt.

Statistische programma’s 16-11
Voorbeeld 2:
Herhaal voorbeeld 1 (met dezelfde gegevens) voor een logaritmische, een
exponentiële en machtcurve. De tabel hieronder geeft u het label waar de
uitvoering start en de resultaten (de correlatie- en regressiecoëfficiënten en de x- en
y- schattingen) voor iedere curve. Elke keer moet u de gegevens opnieuw invoeren
als u het programma opnieuw draait voor een andere curve.
Normale en inverse verdelingen
Normale verdeling wordt vaak gebruikt als model van het gedrag van een
willekeurige variatie rondom een gemiddelde. Dit model veronderstelt dat de
steekproef symmetrisch is om het gemiddelde, M, met een standaarddeviatie, S, en
het resultaat benadert de klokvormige grafiek die u hieronder ziet. Met een
gegeven x kan dit programma de waarschijnlijkheid berekenen, dat een
willekeurige selectie van de gegevens een hogere waarde heeft. Dit heet het upper-
tail area, Q(x). Dit programma doet ook het omgekeerde, met een gegeven waarde
Q(x), berekent het programma de daarmee corresponderende waarde van x.
f/
)
Berekent de regressiecoëfficiënt B.
f/
)
Berekent de regressiecoëfficiënt M.
f%@
)
Vraagt naar hypothetische x-
waarde.
f &@
)
Slaat 37 op in X en berekent .
f %@
) Slaat 101 op in Y en berekent .
Logaritmisch Exponentieel Macht
Start met: WLWEWP
R0,9965 0,9945 0,9959
B –139,0088 51,1312 8,9730
M65,8446 0,0177 0,6640
Y ( als X=37) 98,7508 98,5870 98,6845
X ( als Y=101) 38,2857 38,3628 38,3151
y
ˆ
x
ˆ
y
ˆ
x
ˆ
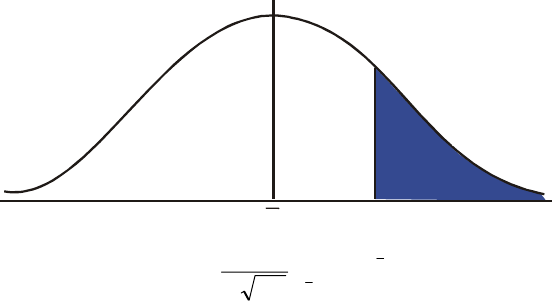
16-12 Statistische programma’s
Dit programma gebruikt het ingebouwde integratieprogramma van de HP 35s om
de vergelijking van de normale verdeling te integreren. De inverse wordt verkregen
met de methode van Newton om iteratief te zoeken naar een waarde van x die de
gegeven waarschijnlijkheid Q(x) oplevert.
x
y
"Upper tail"
area
x
Q [x]
“Upper-tail”
area
∫÷÷−−
−= x
x
xx dxexQ
2))(( 2
2
1
5.0)(
σ
πσ
Statistische programma’s 16-13
Programmalisting:
Programmaregels:
(In de RPN-stand)
Omschrijving
Deze routine initialiseert het programma van de normale
verdeling.
Slaat standaardwaarde voor het gemiddelde op.
!
"! Vraagt om het gemiddelde, M.
Slaat standaardwaarde voor de standaarddeviatie op.
!
"! Vraagt om de standaarddeviatie, S.
! Stopt het weergeven van de waarde van de
standaarddeviatie.
Controlesom en lengte: 70BF 26
Deze routine berekent Q(X) met een gegeven X.
"! %Vraagt om X.
% Berekent upper-tail area.
! Slaat waarde op in Q zodat de functie VIEW hem kan
weergeven.
#$ Geeft Q(X) weer.
! Lus om een andere Q(X) te berekenen.
Controlesom en lengte: 042A 18
Deze routine berekent X met een gegeven Q(X).
"! Vraagt om Q(X).
Roept het gemiddelde op.
! %Slaat het gemiddelde op als schatting voor X, genaamd
Xguess.
Controlesom en lengte: A970 12
! !Dit label markeert de start van de iteratieve lus.
! % Berekent (Q( Xguess)– Q(X)).
! .
! %
! !
! ¶
! % Berekent de afgeleide bij Xguess.
! ª !

16-14 Statistische programma’s
! ªBerekent de correctie voor Xguess.
! !- %Voegt de correctie toe voor een nieuwe Xguess.
!
! )
! º6¸@ Test om te zien of de correctie significant is.
! ! ! Zo ja, ga terug naar het begin van de lus. Zo niet, ga
verder.
! %
! #$ %Geeft de berekende waarden van X weer.
! ! Terug om een andere X te berekenen.
Controlesom en lengte: EDF4 57
Deze subroutine berekent de upper-tail area Q(x).
Roept de ondergrens van de integratie op.
%Roept de bovengrens van de integratie op.
/ Selecteert de functie LBL F voor de integratie.
∫ G Integreert de normale functie met de dummy-variabele D.
π
º
º
º Berekent S ×.
! !Slaat het resultaat tijdelijk op voor de inverse routine.
ª
-+.
)
-Telt de helft van de oppervlakte onder de curve bij omdat
we hebben geïntegreerd met het gemiddelde als
ondergrens.
! Terug naar oproepende routine.
Controlesom en lengte: 8387 52
Deze subroutine berekent de integrand voor de normale
functie
.
Programmaregels:
(In de RPN-stand)
Omschrijving
π
2
2))(( 2÷÷−− SMX
e
Statistische programma’s 16-15
Gebruikte flags:
Geen.
Opmerkingen:
De nauwkeurigheid van dit programma is afhankelijk van de instelling van de
weergave. Bij invoer in het gebied van ±3 standaarddeviaties is een
nauwkeurigheid van vier of meer cijfers voldoende voor de meeste toepassingen.
Bij volledige precisie is de invoergrens ±5 standaarddeviaties. De rekentijd is
aanmerkelijk korter met minder cijfers.
In routine Q, kan de constante 0,5 vervangen worden door 2 en 3.
U hoeft de inverse routine niet in te voeren (in routines I en T) als u daar geen
gebruik van wilt maken.
Programma Instructies:
1. Voer de programmaroutines in; druk op als u klaar bent.
2. Druk op WS.
3. Voer na de prompt voor M het gemiddelde van de populatie in en druk op
f. (Is het gemiddelde nul, druk dan alleen op f.)
ª
º
ª
-+.
H%
! Terug naar oproepende routine.
Controlesom en lengte: B3EB 31
Programmaregels:
(In de RPN-stand)
Omschrijving

16-16 Statistische programma’s
4. Voer na de prompt voor S, de standaarddeviatie in en druk op f. (Is de
standaarddeviatie 1, druk dan alleen op f.)
5. Om X te berekenen met een gegeven Q(X), gaat u verder met stap 9.
6. Om Q(X) te berekenen met een gegeven X, WD.
7. Geef na de prompt de waarde van X op en druk op f. Het resultaat, Q(X),
wordt weergegeven.
8. Om Q(X) te berekenen voor een nieuwe X met hetzelfde gemiddelde en
dezelfde standaarddeviatie, drukt u op f en gaat u naar stap 7.
9. Om X te berekenen met een gegeven Q(X), drukt u op WI.
10. Geef na de prompt de waarde op van Q(X) en druk op f. Het resultaat, X,
wordt weergegeven.
11. Om X te berekenen voor een nieuwe Q(X) met hetzelfde gemiddelde en
dezelfde standaarddeviatie, drukt u op f en gaat u naar stap 10.
Gebruikte variabelen:
Voorbeeld 1:
Uw beste vriend vertelt u dat uw blind date een intelligentie heeft van “3σ”. U
begrijpt daaruit dat ze intelligenter is dan de plaatselijke bevolking, behalve dan
de mensen waarvan de intelligentie meer dan drie standaarddeviaties boven het
gemiddelde ligt.
Nu veronderstelt u dat de plaatselijke bevolking 10.000 mogelijke blind dates
bevat. Hoeveel daarvan hebben een intelligentie van “3σ”? Het probleem is
gegeven in termen van standaarddeviaties, dus we gebruiken een waarde van nul
voor M en 1 voor S.
DDummy-variabele voor integratie.
MGemiddelde van de populatie, standaardwaarde nul.
QWaarschijnlijkheid corresponderend met upper-tail area.
SStandaarddeviatie van de populatie, standaardwaarde 1.
TVariabele die wordt gebruikt om tijdelijk de waarde S × aan
het inverse programma door te geven.
XInvoerwaarde die de linkerkant van upper-tail area definieert.
π
2

16-18 Statistische programma’s
We kunnen dus verwachten dat ongeveer 1 procent van de leerlingen beter scoort
dan 90.
Gegroepeerde standaardafwijking
De standaarddeviatie van gegroepeerde gegevens, Sxy, is de standaarddeviatie
van gegevenspunten x1, x2, ... , xn, die voorkomen bij positieve gehele frequenties
f1, f2, ... , fn.
Invoer:
(In de RPN-stand)
Display: Omschrijving:
WS@
)
Start de initializatieroutine.
f @
)
Geeft 55 als het gemiddelde op.
f ) Geeft 15,3 voor de standaarddeviatie.
WD%@
value
Start het distributieprogramma en
vraagt de waarde van X.
f /
)
Geeft 90 op voor X en berekent Q(X).
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
WI@
)
Start de inverse routine.
f %/
)
Geeft 0,1 (10 procent) in Q(X) en
berekent X.
f@
)
Hervat de inverse routine.
f %/
)
Geeft 0,8 (100 percent min 20
percent) in Q(X) en berekent X.
∑
∑∑
∑
−
−
=1
2
2
)f(
f
)fx(
fx
S
i
i
ii
ii
xg
Statistische programma’s 16-19
Met dit programma kunt u gegevens invoeren, invoer corrigeren evenals de
standaarddeviatie en het gewogen gemiddelde berekenen van de gegroepeerde
gegevens.
Programmalisting:
Programmaregels:
(In de ALG-stand)
Omschrijving
Start het programma voor de gegroepeerde
standaarddeviatie.
; Maakt statistische registers leeg (-27 tot en met -32).
! Maakt de teller N leeg.
Controlesom en lengte: E5BC 13
Invoer van statistische gegevenspunten.
"! %Slaat gegevenspunt op in X.
"! Slaat frequentie van gegevenspunt op in F.
Geeft stapgrootte voor N.
!
Roept de frequentie van gegevenspunt fi terug.
Controlesom en lengte: 3387 19
Accumuleer de sommeringen.
.
! Slaat index op voor register -27.
!-12 Wijzigt in register -27.
h %
! '
.
! Slaat index op voor register -28.
'
!-12 Wijzigt in register -28.
h %
! 'Slaat index op voor register -30.
.
!
'
!-12 Wijzigt in register -30.
∑i
f
iifx
∑iifx
i
2
ifx
∑ii fx 2

16-20 Statistische programma’s
!- Verhoogt (of verlaagt) N.
!
#$ Geeft huidige aantal gegevensparen weer.
! Gaat naar label I voor volgende gegevensinvoer.
Controlesom en lengte: F6CB 84
Berekent statistiek voor gegroepeerde gegevens.
Uº Gegroepeerde standaarddeviatie.
!
#$ Geeft gegroepeerde standaarddeviatie weer.
Gewogen gemiddelde.
!
#$ Geeft gewogen gemiddelde weer.
! Terug voor meer punten.
Controlesom en lengte: DAF2 24
" "Maakt invoerfout ongedaan.
" . Vermindert waarde van N.
" !
" Roept de laatste invoer terug.
" -+. Verandert teken van fi.
" !
" ! Corrigeert telling en sommering.
Controlesom en lengte: 03F4 23
Programmaregels:
(In de ALG-stand)
Omschrijving
º
Statistische programma’s 16-21
Gebruikte flags:
Geen.
Programma Instructies:
1. Voer de programmaroutines in; druk op als u klaar bent.
2. Druk op WS om gegevens in te voeren.
3. Geef op xi -waarde (gegevenspunt) en druk op f.
4. Geef op fi -waarde (frequentie) en druk op f.
5. Druk op f nadat u het aantal ingevoerde punten hebt gezien.
6. Herhaal stap 3 tot en met 5 voor ieder gegevenspunt.
Als u ziet dat u een gegevensinvoer fout gemaakt heeft (xi of fi) nadat u op
f heeft gedrukt in stap 4, druk op WU en druk dan f nog
een keer. Ga dan terug naar stap 3 voor het invoeren van de juiste gegevens.
7. Is het laatste gegevenspaar ingevoerd, druk dan op WG om de
gegroepeerde standaarddeviatie te berekenen.
8. Druk op f om het gewogen gemiddelde van de gegroepeerde gegevens
weer te geven.
9. Om extra gegevens toe te voegen, drukt u op f en gaat u verder met stap
3. Om een nieuw probleem te starten, begint u bij stap 2. Gebruikte
variabelen:
Voorbeeld:
Voer de volgende gegevens in en bereken de gegroepeerde standaarddeviatie.
XGegevenspunt.
FFrequentie van gegevenspunt.
NTeller van gegevenspaar.
SGegroepeerde standaarddeviatie.
MGewogen gemiddelde.
iIndexvariabele om indirect het juiste statistische register te
kunnen adresseren.
Register -27 Sommering Σfi.
Register -28 Sommering Σxifi.
Register -30 Sommering Σxi2fi.
16-22 Statistische programma’s
U gaf voor x3 14 op inplaats van 13. Corrigeer de fout met routine U:
Groep 123456
xi5813152237
fi17 26 37 43 73 115
Invoer:
(In de ALG-stand)
Weergave: Omschrijving:
WS%@
waarde
Vraagt om de eerste xi.
f @
waarde
Slaat 5 op in X; vraagt om de
eerste fi.
f /
)
Slaat 17 op in F; toont de teller.
f%@
)
Vraagt om de tweede xi.
f @
)
Vraagt om de tweede fi.
f /
)
Geeft de teller weer.
f%@
)
Vraagt om de derde xi.
f @
)
Vraagt om de derde fi.
f /
)
Geeft de teller weer.
WU/
)
Verwijdert de verkeerde
gegevens, geeft de verbeterde
teller weer.
f%@
)
Vraagt opnieuw om de derde xi.
f @
)
Vraagt opnieuw om de derde fi.
f/
)
Geeft de teller weer.
f%@
)
Vraagt om de vierde xi.

Statistische programma’s 16-23
f @
)
Vraagt om de vierde fi.
f /
)
Geeft de teller weer.
f%@
)
Vraagt om de vijfde xi.
f @
)
Vraagt om de vijfde fi.
f /
)
Geeft de teller weer.
f%@
)
Vraagt om de zesde xi.
f @
)
Vraagt om de vijfde fi.
f /
)
Geeft de teller weer.
WG /
)
Berekent en toont de
gegroepeerde standaarddeviatie
(sx) van de zes gegevenspunten.
f/
)
Berekent en toont het gewogen
gemiddelde ( ).
) Verwijdert VIEW.
x
Diverse programma’s en vergelijkingen 17-1
17
Diverse programma’s en vergelijkingen
Tijdwaarde van geld
Zijn vier van de vijf waarden in de vergelijking “Tijdwaarde van geld” (TVM)
bekend, dan kunt u de vijfde waarde oplossen. Deze vergelijking is handig voor
diverse financiële toepassingen zoals consumentenleningen en spaarrekeningen.
De TVM-vergelijking is:
De tekens van de bedragen (saldo, B; betaling, P; en toekomstig saldo, F)
corresponderen met de richting van de geldstroom. Ontvangen geld heeft een
positief teken en uitgegeven geld heeft een negatief teken. U ziet dat ieder
probleem vanuit twee perspectieven bekeken kan worden. De geldschieter en de
geldlener zien hetzelfde probleem, maar met een omgekeerd teken.
01001
100
10011 =+++
⎥
⎦
⎤
⎢
⎣
⎡+− −
−B))I((F
I
)I(
PN
N
Saldo, B
Toekomsti
g
e waarde, F
Betalingen, P
N_1
N
123

17-2 Diverse programma’s en vergelijkingen
Invoer van de vergelijking:
Voer deze vergelijking in:
ºº1.1-ª2:.2ª-º1-ª2:.-
Opmerkingen:
De TVM-vergelijking vereist dat I niet nul is om de fout # & te
voorkomen. Lost u I op en twijfelt u over de huidige waarde, druk dan op
{HI voordat u SOLVE start ({I).
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
G ! !
of huidige vergelijking
Selecteert de
vergelijkingenstand.
KPy º _ Start invoer van
vergelijking.
y 4 ºº1.2
4 ºº1.1-22
KIp §º1.1-ª 2 ¨
Õ0§1.1-ª2:2 ¨
_ KNÕ §1-ª2:.2_
p KI KF
y
§2:.2ª-º_
4 KI§:.2ª-º1-2
p Õ§-º1-ª2_
0_ KN§º1-ª2:._
KB§-ª2:.-_
ºº1.1-ª ¨Besluit de vergelijking.
z (vasthouden) /
/
Controlesom en
lengte.
Diverse programma’s en vergelijkingen 17-3
De volgorde waarin om waarden wordt gevraagd is afhankelijk van de variabele
die u oplost.
SOLVE instructies:
1. Wilt u in de eerste TVM-berekening een rentepercentage I oplossen, druk dan
op {HI.
2. Druk op G. Druk zonodig op × of Ø om door de vergelijkingenlijst te
bladeren tot u de TVM-vergelijking vindt.
3. Doe een van de volgende vijf bewerkingen:
a. Druk op {N om het aantal vastgestelde perioden te
berekenen.
b. Druk op {I om de periodieke rente te berekenen.
Voor maandelijkse betalingen, is het resultaat voor I het maandelijkse
rentepercentage, i. Druk op 12 y om het jaarlijkse percentage te
vinden.
c. Druk op {B om een beginbalans van een lening of
spaarrekening te berekenen.
d. Druk op {P om periodieke betaling te berkenen.
e. Druk op {F om de toekomstwaarde of een balans van een
lening te berekenen.
4. Voer de waarden in van de vier bekende variabelen, als erom wordt
gevraagd. Druk na iedere waarde op f.
5. Drukt u op de laatste f, dan wordt de waarde van de onbekende variabele
berekend en weergegeven.
6. Om een nieuwe variabele te berekenen, of dezelfde variabele opnieuw te
berekenen met andere gegevens, gaat u terug naar stap 2.
SOLVE werkt effectief in deze toepassing zonder beginwaarden.

17-4 Diverse programma’s en vergelijkingen
Gebruikte variabelen:
Voorbeeld:
Deel 1. U wilt de aankoop van een auto financieren met een lening van drie jaar
(36 maanden) met een jaarlijks rentepercentage van 10,5%, maandelijks te
betalen. De aankoopprijs van de auto is $7,250. U hebt zelf $1,500.
NHet aantal renteperioden.
IHet periodieke rentepercentage. (Bijvoorbeeld, is de jaarlijkse
rente 15% en zijn er twaalf betalingen per jaar, dan is de
periodieke rentepercentage i, 15÷12=1,25% in.)
BHet startkapitaal van een lening of spaarrekening.
PDe periodieke betaling.
FDe toekomstige waarde van een lening of spaarrekening.
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
8 (%) Selecteert FIX 2 voor de
weergave.
G(Ø zo nodig) ºº1.1-ª¨Geeft het linkerdeel van de
TVM vergelijking weer.
{P@
waarde
Selecteert P; vraagt om I.
p
@
)
Converteert het gegeven
jaarlijkse rentepercentage naar
de maandelijkse waarde.
f@
waarde
Slaat 0,88 op in I; vraagt om
N.
f @
waarde
Slaat 36 op in N; vraagt om F.
B = 7.
2
5
0
_1.5
00
I = 10.5% per jaar
N = 36 maanden F = 0
P =
?
Diverse programma’s en vergelijkingen 17-5
Het antwoord is negatief omdat de lening wordt bekeken vanuit het perspectief van
de lener. Aanvankelijk ontvangt de lener geld en dat is positief. Vervolgens moet er
worden afgelost, en dat is negatief.
f @
waarde
Slaat 0 op in F; vraagt om B.
@
8)
Berekent B, het
uitgangsbedrag.
f #
/
.)
Slaat 5750 op in B; berekent
de maandelijkse betaling, P.
17-6 Diverse programma’s en vergelijkingen
Deel 2. Met welk rentepercentage is het maandelijkse bedrag €10 lager?
Deel 3. Met het gegeven rentepercentage (6,75%) wilt u de auto na twee jaar
verkopen. Wat is uw saldo op dat moment? Met andere woorden, wat is het saldo
na twee jaar?
U ziet dat het rentepercentage, I, uit deel 2 niet nul is, dus u hoeft niet bang te zijn
voor een # & als u de nieuwe I berekent.
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
Gºº1.1-ª¨Geeft het linkerdeel van de TVM
vergelijking weer.
{I@
.)
Selecteert I; vraagt om P.
{ I@
.)
Rondt het bedrag af naar twee
cijfers achter de komma.
@
.)
Berekent nieuwe betaling.
f@
)
Slaat –176,89 op in P; vraagt om
N.
f@
)
Bewaart 36 in N; vraagt om F.
f@
8)
Bewaart 0 in F; vraagt om B.
f #
/
)
Bewaart 5750 in B; berekent
maandelijks rentepercentage.
y ) Berekent jaarlijkse rentepercentage.
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
Gºº1.1-ª¨Geeft het linkerdeel van de TVM
vergelijking weer.
{F@
.)
Selecteert F; vraagt om P.

Diverse programma’s en vergelijkingen 17-7
Generator van priemgetallen
Dit programma begint met een positief getal dat groter is dan 3. Is het een
priemgetal (niet deelbaar door gehele getallen behalve door zichzelf en 1), dan
geeft het programma de ingevoerde waarde terug. Is de invoer geen priemgetal,
dan wordt het eerstvolgende priemgetal teruggegeven.
Het programma herkent priemgetallen door één voor één alle mogelijke factoren te
proberen. Is een getal niet priem, dan telt het programma er 2 bij op (zodat de
waarde nog steeds oneven is) en controleert of het resultaat priem is. Dit proces
gaat door totdat er een priemgetal is gevonden.
f@
)
Bewaart P; vraagt om I.
f@
)
Bewaart 0,56 in I; vraagt om N.
f @
8)
Slaat 24 op in N; vraagt om B.
f #
/
.8)
Bewaart 5750 in B; berekent F, het
toekomstige saldo. Weer is het
teken negatief, dus u moet dit
bedrag nog betalen.
z8
(%)
Stelt FIX 4 weergave formaat in.
Diverse programma’s en vergelijkingen 17-9
Programmalisting:
Programmaregels:
(In de ALG-stand)
Omschrijving
& &Deze routine geeft het priemgetal P weer.
& #$
Controlesom en lengte: 2CC5 6
' 'Deze routine telt 2 bij P op.
' -
Controlesom en lengte: EFB2 9
Deze routine slaat de ingevoerde waarde voor P op.
!º
1ª2
º65¸
º/¸@ Controleer of de invoer even is
-Verhoog P als het even is.
Slaat 3 op in de deler, D
Controlesom en lengte: EA89 47
% %Deze routine onderzoekt of P priem is.
% 1ª2 Berekent het gebroken deel van P ÷ D.
% º/@ Controleert of de rest nul is (niet priem).
% ! ' Als het getal geen priemgetal is, probeert het de
volgende mogelijkheid.
% !12
% º65¸
%
% º>¸@ Controleert of alle mogelijke factoren onderzocht zijn.
% ! & Zijn alle factoren onderzocht, ga dan naar de
uitvoerroutine.
% -
% ! % Ga verder om het getal te onderzoeken met de nieuwe
factor.
Controlesom en lengte: C6B5 53
17-10 Diverse programma’s en vergelijkingen
Gebruikte flags:
Geen.
Programma Instructies:
1. Voer de programmaroutines in; druk op als u klaar bent.
2. Geef een positief getal op groter dan 3.
3. Druk op WP om te beginnen met het programma. Priemgetal P
wordt weergegeven.
4. Druk voor het volgende priemgetal op f.
Gebruikte variabelen:
Opmerkingen:
Er wordt niet gecontroleerd of de invoer groter is dan 3.
Voorbeeld:
Wat is het eerste priemgetal na 789? Wat is het volgende priemgetal?
PPriemwaarde en mogelijke priemwaarden.
DDeler om de huidige waarden van P te onderzoeken.
Invoer:
(In de ALG-stand)
Weergave: Omschrijving:
W
P
/
)
Berekent volgende priemgetal na
789.
f/
)
Berekent volgende priemgetal na
797.

Diverse programma’s en vergelijkingen 17-11
Inwendig product in Vectoren
Hier ziet u een voorbeeld dat u laat zien hoe een programmafunctie gebruikt moet
worden voor berekening van een inwendig product.
Inwendig product:
v1 × v2 = (YW – ZV )i + (ZU – XW)j + (XV – YU)k
waarin
v1 = X i + Y j + Z k
en
v2=U i + V j + W k
Programmaregels:
(In de RPN-stand)
Omschrijving
Definieert het begin van de rechthoekige invoer- en
weergaveroutine.
"! %Toont of accepteert invoer van X.
"! &Toont of accepteert invoer van Y.
"! 'Toont of accepteert invoer van Z.
! Gaat naar R001 voor het invoeren van vectoren
Controlesom en lengte: D82E 15
Definieert het begin van de routine voor invoer van een
vector.
%Kopieert waarden in X, Y en Z respectievelijk naar U, V
en W.
! "
&
! #
'
! $
! Gaat naar R001 voor het invoeren van vectoren
Controlesom en lengte: B6AF 24
17-12 Diverse programma’s en vergelijkingen
Voorbeeld:
Berekent het inwendig product van twee vectoren, v1=2i+5j+4k en v2=i-2j+3k
Programmaregels:
(In de RPN-stand)
Omschrijving
Definieert begin van routine voor inwendig product.
&
º $
'
º #
.Berekent (YW – ZV), dat is de X component.
!
'
º "
%
º $
.Berekent (ZU – WX), dat is de Y component.
!
%
º #
&
º "
.
! 'Slaat (XV – YU) op, dat is de Z component.
! %Slaat X component op.
! &Slaat Y component op.
! Gaat naar R001 voor het invoeren van vectoren
Controlesom en lengte: 838D 72
Diverse programma’s en vergelijkingen 17-13
Invoer: Weergave: Omschrijving:
WR%@
¶DOWH
Start R routine voor de invoer van
een vector waarde
f ¸@
¶DOWH
Voert v2 van x-component in
zfX@
¶DOWH
Voert v2 van y-component in
f %@
Voert v2 van z-component in
WE%@
Begint E routine om V2 in U, V en
W variabelen te wisselen
f ¸@
.
Voert v1 van x-component in
f X@
Voert v1 van y-component in
f %@
Voert v1 van z-component in
WC%@
Start C routine om
Het x-component te berekenen van
een inwendig product
f¸@
.
Berekent het y-component van een
inwendig product
fX@
.
Berekent het z-component van een
inwendig product

Deel 3
Aanhangsels en Referentie

Ondersteuning, batterijen en service A-1
A
Ondersteuning, batterijen en service
Ondersteuning van de rekenmachine
Hebt u vragen over uw rekenmachine, neem dan contact op met onze Calculator
Support Department. Wij weten uit ervaring dat veel klanten dezelfde vragen
hebben over onze producten, en daarom vindt u hieronder “Antwoorden op
veelgestelde vragen”. Vindt u geen antwoord op uw vraag, raadpleeg dan de
Ondersteuningsafdeling, waarvan u het adres vindt op pagina A–8.
Antwoorden op veelgestelde vragen
V: Hoe bepaal ik of de rekenmachine goed functioneert?
A: Op pagina A–5 vindt u een testprogramma.
V: Mijn getallen bevatten komma’s in plaats van punten. Hoe herstel ik dat?
A: Gebruik de functie z85 (5)) (pagina 1–23).
V: Hoe verander ik het aantal decimalen op het scherm?
A: Gebruik het menu z8 (pagina 1–21).
V: Hoe maak ik het geheugen geheel of gedeeltelijk leeg?
A:{ toont het CLEAR menu, welke u x leeg laat maken (het getal in het
X-register), alle directe variabelen, al het geheugen, alle statische gegevens, alle
stapelniveau’s en alle indirecte variabelen.
V: Wat betekent een “E” in een getal (bijvoorbeeld, ).)?

A-2 Ondersteuning, batterijen en service
A: Exponent van tien; dus 2,51 × 10–13.
V: De rekenmachine geeft het bericht & ". Wat nu?
A: Wis een deel van het geheugen voor u verdergaat. (Zie aanhangsel B.)
V: Bij het berekenen van de sinus (of tangens) van π radialen krijg ik een heel klein
getal in plaats van 0. Hoe komt dat 0?
A: π kan niet precies gerepresenteerd worden binnen de 12-cijferige precisie van
de rekenmachine.
V: Waarom krijg ik onjuiste antwoorden bij de trigonometrische functies?
A: Zorg ervoor dat de rekenmachine de juiste hoekeenheden gebruikt (9
, , of ).
V: Wat betekent een annunciator op het scherm?
A: Hij geeft iets aan over de toestand van de rekenmachine. Zie “Annunciators” in
hoofdstuk 1.
V: getallen verschijnen als breuken. Hoe krijg ik weer decimale getallen?
A: Druk op { .
Bedrijfsomgeving
Voor een betrouwbare werking, dienen onderstaande temperaturen en
vochtigheidsgraden in acht genomen te worden:
Bedrijfstemperatuur: van 0 tot 45°C (van 32 tot 113°F).
Opslagtemperatuur: van –20 tot 65°C (van –4 tot 149°F).
Opslag- en bedrijfsvochtigheid: maximaal 90% relatieve vochtigheid bij
40°C (104°F).

Ondersteuning, batterijen en service A-3
De batterijen vervangen
De rekenmachine werkt op twee lithiumbatterijen van 3 volt, type CR2032.
Vervang de batterijen zo snel mogelijk als de annunciator (¤) aangeeft dat de
batterij bijna leeg is. Ziet u deze annunciator, en wordt het scherm zwakker, dan
zou u gegevens kunnen verliezen. Gaan de gegevens verloren, dan verschijnt de
melding & .
Hebt u de batterijen verwijderd, vervang ze dan binnen 2 minuten om te
voorkomen dat u gegevens verliest. (Zorg ervoor dat u de nieuwe batterijen bij de
hand hebt voor u het batterijvak opent.)
Batterijen plaatsen:
1. Zorg ervoor dat u twee verse knoopbatterijen bij de hand hebt. Raak de
aansluitingen van de batterijen niet aan — houd de batterijen bij de randen
vast.
2. Zorg ervoor dat de rekenmachine UIT staat. Druk niet weer op (Å)
voordat de nieuwe batterijen geplaatst zijn. Staat de
rekenmachine AAN zonder batterijen, dan gaat de inhoud van
het continue geheugen verloren.
3. Draai de rekenmachine om en open het batterijvak.
4. Om geheugenverlies te voorkomen, verwijder nooit twee batterijen op
hetzelfde moment. Verwijder en vervang elke keer maar een batterij.

A-4 Ondersteuning, batterijen en service
5. Plaats een nieuwe CR2032 lithium-batterij, met het plusteken (+) aan de
buitenkant.
6. Vervang nu de andere batterij zoals in stap 4 tot en met 5. Let erop dat het
plusteken (+) naar buiten wijst.
7. Sluit het deksel van het batterijvak.
8. Druk op .
De werking van de rekenmachine controleren
Gebruik de volgende richtlijnen om vast te stellen of de rekenmachine goed
functioneert. Test de rekenmachine na iedere stap om vast te stellen of hij nog goed
werkt. Moet de rekenmachine gerepareerd worden, lees dan pagina A–8.
De rekenmachine laat zich niet inschakelen (stappen 1–4) of reageert niet als
u op toetsen drukt (stappen 1–3):
1. Reset de rekenmachine. Houd de toets ingedrukt en druk op U.
Het kan nodig zijn deze toetsaanslagen een paar keer te herhalen.
2. Wis het geheugen. Houd ingedrukt en houd daarna tegelijkertijd
f en 6 ingedrukt. Het geheugen wordt gewist en het bericht
& verschijnt als u de drie toetsen loslaat.
Let op Beschadig en doorboor de batterijen niet en gooi ze niet in
het vuur. De batterijen kunnen barsten of exploderen,
waarbij milieuvervuilende stoffen vrijkomen.

Ondersteuning, batterijen en service A-5
3. Verwijder de batterijen (zie “De batterijen vervangen”) en druk zachtjes
met een munt op de twee batterijcontacten in de rekenmachine. Doe de
batterijen terug en zet de rekenmachine aan. U ziet de tekst &
.
4. Als de rekenmachine nog steeds niet reageert op de toetsaanslagen,
gebruik een dun, scherp objebt en druk op het RESET gaatje. Opgeslagen
gegevens blijven meestal intact.
Resetgaatje
Als deze stappen niet helpen om het gebruik van de rekenmachine te
herstellen, dan moet de rekenmachine gerepareerd worden.
Als de rekenmachine reageert op toetsaanslagen maar u denkt dat er iets
mis is:
1. Voer de hierna beschreven test uit. Mislukt de test, dan moet de
rekenmachine gerepareerd worden.
2. Als de test lukt, heeft u misschien een fout gemaakt tijdens het gebruik van
de rekenmachine. Lees gedeeltes van de handleiding opnieuw en
controleer “Antwoorden op Normale Vragen (Pagina A–1).
3. Raadpleeg de Ondersteuningsafdeling waarvan u het adres vindt op
pagina A–8.
De zelftest
Als het scherm aangezet kan worden, maar de rekenmachine schijnt niet goed te
werken, doe dan de volgende diagnostische zelftest.
1. Houd de toets ingedrukt en druk tegelijk op W.
2. Druk een willekeurige toets acht keer ingedrukt en let op de getoonde
patronen. Nadat u een toets acht keer hebt ingedrukt, toont de rekenmachine
het auteursrecht © # ) ) ) en daarna .
3. Druk de toetsen in de volgende volgorde:
A-6 Ondersteuning, batterijen en service
f△U△W△9 △× △ Ö △Õ △ K△9△
Z△6 △ Ø△N△Q△T △ < △ 0 △ 3△
△_△△4△@△G△ △ △ △p△z
△△ △ △y △ {△△△△△ △
△ △ 6△
Drukt u de toetsen in de juiste volgorde in en functioneren ze goed, dan
verschijnt de tekst gevolgd door getallen van twee cijfers. (De
rekenmachine telt de toetsen hexadecimaal.)
Drukt u in de verkeerde volgorde op een toets, of functioneert een toets
niet goed, dan verschijnt er bij de volgende toets een foutmelding (zie
stap 4).
4. De zelftest geeft een van de volgende twee resultaten:
De rekenmachine toont . als de test geslaagd is. Ga naar stap 5.
De rekenmachine toont . gevolgd door een cijfer als de test
mislukt is. Als dat komt omdat u de toetsen in de verkeerde volgorde
indrukte, reset de rekenmachine dan (houd ingedrukt en druk op
U) en voer de zelftest opnieuw uit. Als u deze melding krijgt, hoewel u
de toetsen in de juiste volgorde indrukte, herhaal de zelftest dan om dit
zeker te weten. Mislukt de test dan opnieuw, dan moet de rekenmachine
gerepareerd worden (zie pagina A-8). Verzendt u de rekenmachine voor
reparatie, sluit dan een kopie van het FAIL-bericht bij.
5. Als u de zelftest wilt beëindigen, reset u de rekenmachine (houd ingedrukt
en druk op U).
Door te drukken op en 9 wordt er een continue zelftest gestart die in de
fabriek wordt gebruikt. Deze test kunt u stoppen door op een willekeurige toets te
drukken.

Ondersteuning, batterijen en service A-7
Garantie
HP 35s wetenschappelijke rekenmachine; garantieperiode: 12 maanden
1. HP garandeert u, klant en gebruiker, dat de hardware, onderdelen en
toebehoren van HP vrij zijn van defecten aan materiaal en constructie vanaf de
datum van aankoop en voor de hierboven vermelde duur. Ontvangt HP binnen
de garantieperiode een bericht van een dergelijk defect, dan zal HP, naar
keuze, het defecte product repareren of vervangen. Vervangingsonderdelen
zullen nieuw of zo goed als nieuw zijn.
2. HP garandeert u dat de HP-software de programmeerinstructies goed zal
uitvoeren vanaf de datum van aankoop en voor de hierboven vermelde duur,
mits correct geïnstalleerd en behandeld. Ontvangt HP binnen de
garantieperiode een bericht van een dergelijk defect, dan zal HP de software
vervangen die door dit defect de programmeerinstructies niet goed uitvoert.
3. HP garandeert niet dat de werking van HP-producten foutloos en vrij van
onderbrekingen is. Is HP niet in staat binnen een redelijke termijn een product
te repareren of te vervangen, waarmee het weer binnen de
garantievoorwaarden valt, dan heeft de koper, tegen teruggave van het
product, recht op teruggave van de aankoopprijs met aanschafbonnetje.
4. HP-producten kunnen onderdelen bevatten die zo goed als nieuw functioneren
of incidenteel gebruikt zijn geweest.
5. De garantie is niet van toepassing op defecten die voortvloeien uit (a) onjuist of
onvoldoende onderhoud of kalibratie, (b) software, interfaces, onderdelen die
niet door HP zijn geleverd, (c) onbevoegde wijziging of misbruik, (d) gebruik
buiten de opgegeven omgevingscondities voor het product, of (e)
ondeskundige voorbereiding of onderhoud.

A-8 Ondersteuning, batterijen en service
6. HP GEEFT GEEN ANDERE UITDRUKKELIJKE GARANTIE, SCHRIFTELIJK NOCH
MONDELING, VOORZOVER NIET VEREIST DOOR LOKALE WETGEVING.
IEDERE IMPLICIETE GARANTIE VAN GESCHIKTHEID VOOR VERKOOP,
BEVREDIGENDE KWALITEIT, GESCHIKTHEID VOOR EEN BEPAALD DOEL IS
BEPERKT TOT DE UITDRUKKELIJKE HIERBOVEN BESCHREVEN GARANTIE.
Sommige landen, staten en provincies staan een beperkte impliciete garantie
niet toe, zodat de hierboven genoemde beperking voor u niet van toepassing
hoeft te zijn. Deze garantie geeft u bepaalde wettelijke rechten en u zou nog
meer rechten kunnen hebben die van land tot land, van staat tot staat of van
provincie tot provincie verschillen.
7. BINNEN DE BEPERKINGEN DIE ZIJN TOEGESTAAN DOOR DE LOKALE
WETGEVING, ZIJN ER GEEN GARANTIEMOGELIJKHEDEN, BEHALVE DE
HIERBOVEN VERMELDE. BEHALVE VOOR DE HIERBOVEN VERMELDE
GEVALLEN, ZIJN HP NOCH ZIJN WEDERVERKOPERS AANSPRAKELIJK
VOOR VERLIES VAN GEGEVENS OF VOOR DIRECTE, SPECIALE,
INCIDENTELE, CONSEQUENTIËLE EN ANDERE SCHADE, INCLUSIEF
WINSTDERVING, VOLGENS DE VERMELDING IN HET CONTRACT OF
ANDERSZINS. Sommige landen, Staten of provincies laten de uitzondering of
beperking van incidentele of consequentiële schade niet toe, dus de hierboven
vermelde beperking of uitzondering is misschien niet voor u van toepassing.
8. De enige garanties voor HP-producten en -diensten staan vermeld in de
uitdrukkelijke garantieverklaringen die bij die producten en diensten worden
geleverd. Verder kan niets worden opgevat als een extra garantie. HP is niet
verantwoordelijk voor technische fouten en schrijffouten in de documentatie.
VOOR CONSUMENTENTRANSACTIES IN AUSTRALIË EN NIEUW
ZEELAND: DE GARANTIEVOORWAARDEN IN DIT DOCUMENT,
VOORZOVER WETTELIJK TOEGESTAAN, BETEKENEN GEEN
UITSLUITING, BEPERKING OF WIJZIGING EN ZIJN SLECHTS EEN
UITBREIDING VAN DE VERPLICHTE STATUTAIRE RECHTEN DIE VAN
TOEPASSING ZIJN OP DE VERKOOP VAN DIT PRODUCT AAN U.
Klantenondersteuning
AP Land: Telefoonnummer
Australië 1300-551-664 of
03-9841-5211

Ondersteuning, batterijen en service A-9
China 010-68002397
Hong Kong 2805-2563
Indonesië +65 6100 6682
Japan +852 2805-2563
Maleisië +65 6100 6682
Nieuw-Zeeland 09-574-2700
Filippijnen +65 6100 6682
Singapore 6100 6682
Zuid-korea 2-561-2700
Taiwan +852 2805-2563
Thailand +65 6100 6682
Vietnam +65 6100 6682
EMEA (Europa,
Midden-
Oosten en
Africa)
Land: Telefoonnummer
Austria 01 360 277 1203
België 02 620 00 86
België 02 620 00 85
Turkije 296 335 612
Denemarken 82 33 28 44
Finland 09 8171 0281
Frankrijk 01 4993 9006
Duitsland 069 9530 7103
Griekenland 210 969 6421
Nederland 020 654 5301
Ierland 01 605 0356
Italië 02 754 19 782
Luxembourg 2730 2146
Noorwegen 23500027
Portugal 021 318 0093
Rusland 495 228 3050
Zuidelijk Afrika 0800980410
Spanje 913753382
Zweden 08 5199 2065
Zwitserland 022 827 8780 (Frans)

A-10 Ondersteuning, batterijen en service
Zwitserland 01 439 5358 (Duits)
Zwitserland 022 567 5308 (Italiaans)
Verenigd Koninkrijk 0207 458 0161
LA Land: Telefoonnummer
Anguila 1-800-711-2884
Antenne 1-800-711-2884
Argentinië 0-800- 555-5000
Aruba 800-8000 ♦ 800-711-2884
Bahamas 1-800-711-2884
Barbados 1-800-711-2884
Bermuda 1-800-711-2884
Bolivia 800-100-193
Brazilië 0-800-709-7751
Britse maagdeneilanden 1-800-711-2884
Kaaiman eiland 1-800-711-2884
Curacao 001-800-872-2881 +
800-711-2884
Chili 800-360-999
Colombië 01-8000-51-4746-8368
(01-8000-51- HP INVENT)
Costa Rica 0-800-011-0524
Dominica 1-800-711-2884
Dominicaanse Republiek 1-800-711-2884
Ecuador 1-999-119 ♦ 800-711-2884
(Andinatel)
1-800-225-528 ♦ 800-711-2884
(Pacifitel)
El Salvador 800-6160
Franse Antillen 0-800-990-011♦ 800-711-2884
Frans Guiana 0-800-990-011♦ 800-711-2884
Grenada 1-800-711-2884
Guadelupe 0-800-990-011♦ 800-711-2884
Guatemala 1-800-999-5105
Guyana 159 ♦ 800-711-2884

Ondersteuning, batterijen en service A-11
Haïti 183 ♦ 800-711-2884
Honduras 800-0-123 ♦ 800-711-2884
Jamaica 1-800-711-2884
Martinica 0-800-990-011 ♦ 877-219-8671
Mexico 01-800-474-68368 (800 HP
INVENT)
Montserrat 1-800-711-2884
Nederlandse Antillen 001-800-872-2881 ♦
800-711-2884
Nicaragua 1-800-0164 ♦ 800-711-2884
Panama 001-800-711-2884
Paraguay (009) 800-541-0006
Perú 0-800-10111
Puerto Rico 1-877 232 0589
St. Lucia 1-800-478-4602
St. Vincent 01-800-711-2884
St. Kitts&Nevis 1-800-711-2884
St. Maarten 1-800-711-2884
Suriname 156 ♦ 800-711-2884
Trinidad & Tobago 1-800-711-2884
Turks & Caicos 01-800-711-2884
US Maagdeneilanden 1-800-711-2884
Uruguay 0004-054-177
Venezuela 0-800-474-68368 (0-800 HP
INVENT)
Noord
Amerika
Land: Telefoonnummer
Canada 800-HP-INVENT
USA 800-HP INVENT
Ga naar http://www.hp.com voor de laatste informatie over onze service en
ondersteuning.

A-12 Ondersteuning, batterijen en service
Gereguleerde informatie
Federale communicatie commissie opmerking
Dit toestel werd getest en bevonden overeen te stemmen met de limieten voor een
klasse B digitaal toestel, overeenkomstig met deel 15 van de FCC regels. Deze
limieten werden ontworpen om een redelijke bescherming te bieden tegen
schadelijke stoornissen in een residentiële installatie. Deze apparatuur brengt voort,
gebruikt en kan radio frequentie energie uitstralen, en indien niet geïnstalleerd en
gebruikt in overeenstemming met de instructies, zou schadelijke stoornissen kuinnen
veroorzaken aan radio communicaties. Maar er is geen waarborg dat stoornissen
niet zullen optreden tijdens een welbepaalde installatie. Als deze apparatuur enige
schadelijke stoornissen veroorzaakt voor de ontvangst van radio- of televisie
signalen, dan wordt de gebruiker aangespoord om dit te corrigeren. De stoornis
wordt bepaald door de apparatuur aan- en uit te schakelen. De gebuiker kan de
stoornis verhelpen door een of meerdere van de volgende maatregelen toe te
passen:
• Heroriënteer of verplaats de ontvangende antenne.
• Vergroot de afstand tussen de apparatuur en de ontvanger.
• Verbind de apparatuur met een stopcontact, dat verschilt van datgene
waarmee de ontvanger is verbonden.
• Contacteer de verkoper of een ervaren radio- of televisie technicus voor
help.
Aanpassingen
Het FCC vereist dat de gebruiker op de hoogte wordt gebracht van het feit dat
enige veranderingen of aanpassingen aan dit toestel, die niet uitdrukkelijk worden
goedgekeurd door Hewlett-Packard, de bevoegdheid van de gebruiker om het
apparaat te bedienen, teniet kunnen doen.
Verklaring van overeenkomstigheid
Voor produkten gekenmerkt met een FCC logo
Enkel in de Verenigde Staten
Dit toestel komt overeen met deel 15 van de FCC regels. De bediening is
onderhevig aan de volgende twee voorwaarden: (1) dit toestel mag geen
schadelijke stoornissen veroorzaken en (2) dit toestel moet enige ontvangen
stoornissen aanvaarden, met inbegrip van stoornissen die een ongewenste
bediening kunnen veroorzaken.
Als u enige vragen heeft over het produkt, die niets te maken hebben met deze
verklaring, schrijf dan naar

Ondersteuning, batterijen en service A-13
Hewlett-Packard Company
P.O. Box 692000, Mail Stop 530113
Houston, TX 77269-2000
Voor vragen betreffende deze FCC verklaring, schrijf naar
Hewlett-Packard Company
P.O. Box 692000, Mail Stop 510101
Houston, TX 77269-2000
of bel naar HP op 281-514-3333
Om uw produkt te identificeren, verwijs naar het deel, series, of modelnummer, dat
zich op de achterkant van het produkt bevindt.
Opmerking voor Canada
Dit klasse B digitaal toestel komt tegemoet aan alle vereisten van de Canadese
wetgeving voor stoornissen veroorzakende apparatuur.
Avis Canadien
Cet appareil numérique de la classe B respecte toutes les exigences du Règlement
sur le matériel brouilleur du Canada.
Gereguleerde opmerking van de Europese Unie
Dit produkt komt overeen met de volgende richtlijnen van de EU:
• Lage Voltage Richtlijn 2006/95/EC
• EMC richtlijn 2004/108/EC
Overeenkomstigheid met deze richtlijnen houdt overeenstemming in met toepasbare
overeenkomstige Europese standaarden (Europese Normen), die worden
weergegeven op de EU verklaring van overeenkomstigheid, uitgevaardigd door
Hewlett-Packard voor dit produkt of produkt familie.
Deze overeenkomstigheid wordt aangegeven door het volgende
overeenkomstigheids- merkteken, dat op het produkt wordt geplaatst:
Hewlett-Packard GmbH, HQ-TRE, Herrenberger Strasse 140, 71034, Boeblingen,
Duitsland
This marking is valid for non-Telecom products
and EU harmonized Telecom products
(e.g. Bluetooth).
This marking is valid for EU non-harmonized
Telecom products.
*Notified body number (used only if
applicable - refer to the product label)
yyyy+

A-14 Ondersteuning, batterijen en service
Japanese Notice
この装置は、 情報処理装置等電波障害自主規制協議会 (VCCI) の基準に基づ く ク
ラ ス B 情報技術装置です。 この装置は、 家庭環境で使用する こ と を目的 と し てい
ますが、 こ の装置が ラ ジオやテ レ ビ ジ ョ ン受信機に近接 し て使用 さ れる と 、 受信
障害を引き起 こ す こ と があ り ま す。
取扱説明書に従っ て正 し い取 り 扱いを し て く だ さ い。
Verwijdering van afgedankte apparatuur door privé-
gebruikers in de Europese Unie
Dit symbool op het product of de verpakking geeft aan dat dit
product niet mag worden gedeponeerd bij het normale
huishoudelijke afval. U bent zelf verantwoordelijk voor het inleveren
van uw afgedankte apparatuur bij een inzamelingspunt voor het
recyclen van oude elektrische en elektronische apparatuur. Door uw
oude apparatuur apart aan te bieden en te recyclen, kunnen
natuurlijke bronnen worden behouden en kan het materiaal worden
hergebruikt op een manier waarmee de volksgezondheid en het milieu worden
beschermd. Neem contact op met uw gemeente, het afvalinzamelingsbedrijf of de
winkel waar u het product hebt gekocht voor meer informatie over
inzamelingspunten waar u oude apparatuur kunt aanbieden voor recycling.
Perchloraat Materiaal- speciale behandeling is misschien nodig
De geheugen Backup batterij van de rekenmachine kan perchloraat bevatten en
moet misschien speciaal worden behandeld wanneer het verwijderd of hercycled
wordt in Californië.

Het gebruikersgeheugen en de stapel B-1
B
Het gebruikersgeheugen en de stapel
Dit aanhangsel bespreekt
Toekenning en vereisten van het gebruikersgeheugen,
Hoe u de rekenmachine reset zonder het geheugen te wissen,
Hoe u het volledige geheugen wist en de systeemstandaarden terugroept, en
Welke bewerkingen de stapel optillen.
Het geheugen beheren
De HP 35s heeft 30KB gebruikersgeheugen dat beschikbaar is voor opgeslagen
gegevens (variabelen, vergelijkingen of programmaregels). SOLVE, ∫ FN, en
statistishe berekeningen hebben ook geheugen nodig. (De bewerking ∫ FN neemt
bijzonder “veel geheugen in beslag”.)
Al uw opgeslagen gegevens blijven behouden tot u ze uitdrukkeljik verwijdert. Het
bericht & " betekent dat er momenteel niet genoeg geheugen is voor
de gevraagde bewerking. U moet dan wat geheugen vrijmaken. U kunt
bijvoorbeeld:
Vergelijkingen verwijderen (zie “Vergelijkingen bewerken en wissen” in
hoofdstuk 6).
Programma’s verwijderen (zie “Een of meer programma’s wissen” in
hoofdstuk 13).
Het hele geheugen wissen (druk op { ()).
Om te weten hoeveel geheugen er beschikbaar is, drukt u op zX. Het
scherm geeft het aantal bytes weer.

B-2 Het gebruikersgeheugen en de stapel
Om de geheugenvereisten te zien van specifieke vergelijkingen in de
vergelijkingenlijst:
1. Druk op G om de vergelijkingenstand te openen. ( ! ! of de
linkerkant van de huidige vergelijking wordt weergegeven.)
2. Schuif zonodig door de vergelijkingenlijst (druk op × of Ø) tot u de
gewenste vergelijking ziet.
3. Druk op z voor de controlesom (hexadecimaal) en de lengte (in
bytes) van de vergelijking. Bijvoorbeeld, / /.
Als u het totale geheugenverbruik van een specifiek programma wilt zien:
1. Druk op z X () om het eerste label in de programmalijst te
tonen.
2. Blader door de programmalijst (met × of Ø) tot u de grootte van het
gewenste programma ziet. Bijvoorbeeld, /.
3. Eventueel: Druk op z om de controlesom (hexadecimaal) en lengte
(in bytes) van het programma te zien. Bijvoorbeeld, / /.
Als u het geheugenverbruik van een vergelijking in een programma wilt zien:
1. Geef de programmaregel met de vergelijking weer.
2. Druk op z m de controlesom en lengte te zien. Bijvoorbeeld,
/ /.
De rekenmachine resetten
Als de rekenmachine niet reageert op toetsaanslagen of op een andere manier
vreemd reageert, probeer het dan te resetten. Het resetten van de rekenmachine
breekt de huidige berekening af en stopt de programma invoer, cijfer invoer, een
werkend programma, een SOLVE berekening, een ∫ FN berekening, een VIEW
weergave, of een INPUT weergave, Opgeslagen gegevens blijven normaal
gesproken intact.
Om de rekenmachine te resetten, houd u de toets ingedrukt en drukt u U.
Lukt het resetten niet, plaats dan nieuwe batterijen. Lukt reset dan nog niet, of
functioneert hij niet goed, maak dan het geheugen leeg met de speciale procedure
hieronder.
Als de rekenmachine nog steeds niet reageert op toetsaanslagen, gebruik dan een
dun, scherp object om het RESET gaatje mee in te drukken.
De rekenmachine kan zichzelf resetten als hij valt of als de voeding tijdelijk
onderbroken wordt.

Het gebruikersgeheugen en de stapel B-3
Geheugen wissen
De gebruikelijke manier om het gebruikersgeheugen te wissen is met {
(). Er is echter een krachtigere methode die ook extra informatie
reset en die handig is als het toetsenbord niet goed functioneert.
Als de rekenmachine niet reageert op toetsaanslagen, en u bent niet in staat om
gebruik te hervatten door het te resetten of de batterijen te vervangen, probeer dan
de volgende GEHEUGEN WISSEN procedure. Deze toetsaanslagen wissen al het
geheugen, resetten de rekenmachine en zetten alle standen terug in hun
oorspronkelijke standaard instelling (hieronder getoond)
1. Houd de toets ingedrukt.
2. Houd de toets ¥ ingedrukt.
3. Druk op 6. (Er zijn nu drie toetsen tegelijkertijd ingedrukt). Laat u de drie
toetsen los, dan verschijnt & in geval de bewerking succesvol
was.

Het gebruikersgeheugen en de stapel B-5
Uitschakelende bewerkingen
De vijf bewerkingen , /, -, {(%) en {
( !) schakelen het optillen van de stapel uit. Een getal ingetoetst na een van
deze uitgeschakelde bewerkingen schrijft het getal over dat zich nu in het X–register
bevindt. De Y–, Z– en T–registers blijven.
Verder, als en a zich gedragen als CLx, dan schakelen ze ook het optillen
uit.
De INPUT-functie schakelt het optillen uit als hij een programma onderbreekt voor
invoer (elk getal overschrijft dus het X register), maar het optillen wordt weer
ingeschakeld als het programma verder gaat.
Neutrale bewerkingen
De volgende bewerkingen hebben geen invloed op het optillen van de stapel:
DEG, RAD,
GRAD
FIX, SCI,
ENG, ALL
DEC, HEX,
OCT, BIN
CLVARS
PSE SHOW RADIX . RADIX , CLΣ
hf en STOP × en Ø* en a*
X
(1#)**
X
(2)**
U U
label nnn
EQN FDISP Fouten d en
programmainvoer
Binaire vensters
schuiven
Cijferinvoer xiy r
θ
a :
Behalve indien gebruikt als CLx.
Inclusief alle bewerkingen die worden uitgevoerd als de catalogus wordt
weergegeven, behalve {#} en {} W, die het optillen
inschakelen.

B-6 Het gebruikersgeheugen en de stapel
De toestand van het register LAST X
De volgende bewerkingen slaan x op in het LAST -X register in de RPN stand:
De bewerking /c heeft geen invloed op LAST X.
De oproep-berekeningssequentie Xh variabele slaat x op in LASTx en
Xh variabele slaat het opgeroepen getal op in LASTx.
In de ALG stand, is de LAST X register een partner voor de stapel: het houdt het
getal dat het resultaat is van de laatste expressie. Het ondersteunt het gebruik van
het vorige expressie resultaat in de ALG stand.
+, –, × , ÷, x2, ex, 10x
LN, LOG yx, I/x, INT÷, Rmdr
SIN, COS, TAN ASIN, ACOS, ATAN
SINH, COSH, TANH ASINH, ACOSH, ATANH IP, FP, SGN, INTG,
RND, ABS
%, %CHG Σ+, Σ–RCL+, –, ×, ÷
HMS, HMS DEG, RAD
nCr nPr ! ARG
CMPLX +, –, × ,÷CMPLX ex, LN, yx, 1/x CMPLX SIN, COS,
TAN
kg, lb
l, gal
°C, °F
KM MILE
cm, in
x
Xy
º
ˆ¸
ˆ

Het gebruikersgeheugen en de stapel B-7
Stapel Register Inhoud
De waarden die worden gehouden in de vier stapel registers X, Y, Z en T, zijn
toegangbaar in de RPN stand in een vergelijking of programma met de REGX,
REGY, REGZ en REGT commando’s.
Om deze instructies te gebruiken, druk eerst op d. Dan, drukken op < maakt
een menu in het scherm dat de X-, Y-, Z-, T- registers weergeeft. Drukken op Õ of
Ö verplaatst het onderstrepingssymbool, aangevend welk register nu is
geselecteerd. Drukken op plaatst een instructie in een programma of
vergelijking dat de waarden van de gekozen stapel register oproept voor verder
gebruikt. Deze worden weergegeven als REGX, REGY, REGZ, en REGT.
Bijvoorbeeld, een programmaregel ingevoerd door eerst drukken op d en dan
door het invoeren van de instructies REGX x REGY x REGZ x REGT zal het product
van de waarden in de 4 stapel registers berekenen en het resultaat plaatsen in het
X-register. Het laat de vorige waarden van X,Y en Z in de stapel registers Y, Z en T.
Veel van deze efficiente toepassingen van waarden in de stapel zijn op deze
manier mogelijk dat anders niet beschikbaar zou zijn in de HP35s.

ALG: Samenvatting C-1
C
ALG: Samenvatting
Informatie over ALG
Dit aanhangsel geeft een samenvatting van enkele mogelijkheden die uniek zijn
voor ALG, waaronder:
Rekenen met twee getallen
Exponentiële en logarithmische functies (z(,z+, {
*,{-)
Trigonometrische functies
Delen van getallen
De stapel bekijken
Bewerkingen met complexe getallen
Een vergelijking integreren
Rekenen met talstelsels 2, 8 en 16
Statistische gegevens met twee variabelen invoeren
Druk op 9() om de rekenmachine in de stand ALG te zetten. U ziet
nu de annunciator ALG.
In de ALG-stand worden bewerkingen met de volgende prioriteit uitgevoerd:
1. Bewerkingen tussen haakjes.
2. Factoriale (!) notatie vereist het invoeren van waarden voordat u op * drukt.
3. Functies die het invoeren van waarden vereisen na het drukken van de functie
toets, bijvoorbeeld, COS, SIN, TAN, ACOS, ASIN, ATAN, LOG, LN, x2, 1/x,
, π, , %, RND, RAND, IP, FP, INTG, SGN, nPr, nCr, %CHG, INT÷,
Rmdr, ABS, ex,10x, eenheid conversie.
x3x

C-2 ALG: Samenvatting
4. en yx.
5. Minteken met één operand +/-
6. ×, ÷
7. +, –
8. =
Rekenen met twee getallen in ALG
Deze discussie van rekenen met ALG vervangt de volgende delen die zijn beinvloed
door de ALG stand. Berekeningen met twee getallen zijn beïnvloed door de ALG
stand:
Eenvoudig rekenen
Machtfuncties (0, .)
Percentageberekeningen (P of { S)
Permutaties en combinaties (z x, { {)
Quotiënt en rest bij deling (zJ(!÷),
zJ(PGT))
Eenvoudig rekenen
Hier zijn een paar voorbeelden van eenvoudig rekenen. Let op het volgende.
In de stand ALG geeft u eerst het eerste getal op, gevolgd door de operator (,
, y, p), het tweede getal en tenslotte de toets .
Om te berekenen: Drukt u op: Weergave:
12 + 3 -
)
12 – 3 .
)
12 × 3 y º
)
12 ÷ 3p ª
)
xy

ALG: Samenvatting C-3
Machtfuncties
In de stand ALG berekent u y in de macht x met y 0 x, gevolgd door .
Percentageberekeningen
De procentfunctie. De toets P deelt een getal door 100.
Voorbeeld:
Stel dat het $15,76 objekt het afgelopen jaar $16,12 kostte. Wat is de prijs dan
percentagewijs veranderd met het afgelopen jaar?
Om te berekenen: Drukt u op: Weergave:
1230 :
8)
641/3 (derdemachts
wortel)
z.Õ64
%!182
)
Om te berekenen: Drukt u op: Weergave:
27% van 200 {PÕ2
7
0182
)
200 minus 27% {P
Õ27
.0182
)
25 plus 12% {P
Õ12
-0182
)
Om te berekenen: Drukt u op:
x% of y{P y Õ x
Procentuele verandering van y naar x. (y≠
0)
zS y Õx
Invoer: Weergave: Omschrijving:
zS
Õ
01)8)
.)
Dit jaar is de prijs 2,2%
gezakt van de prijs van het
afgelopen jaar.

C-4 ALG: Samenvatting
Permutaties en combinaties
Voorbeeld: Combinaties van personen.
Een bedrijf dat 14 vrouwen 10 mannen in dienst heeft, vormt nu een
veiligheidscommissie bestaande uit zes personen.Hoeveel verschillende combinaties
van mensen zijn er mogelijk?
Quotiënt en rest bij deling
U kunt zJ(!÷) en zJ(PGT) gebruiken om het
quotiënt of de rest te bepalen als er twee gehele getallen worden gedeeld.
zJ(!÷)Geheel getal 1 Õ Geheel getal 2.
zJ(PGT)Geheel getal 1 Õ Geheel getal 2.
Voorbeeld:
Voor het weergeven van quotiënt en de rest geproduceerd door 58÷ 9.
Berekeningen met haakjes
Gebruik haakjes als u een berekening van een gemiddeld resultaat wilt uitstellen
totdat u meer getallen heeft ingevoerd. Bijvoorbeeld, stel dat u wilt berekenen:
Invoer: Weergave: Omschrijving:
zxÕ
QT182
8)
Totaal aantal mogelijke
combinaties.
Invoer: Weergave: Omschrijving:
zJ(!÷)
Õ9
#182
)
Geeft het quotiënt weer.
zJ(PGT)
Õ9
182
)
Geeft de rest weer.
9
1285
30 ×
−
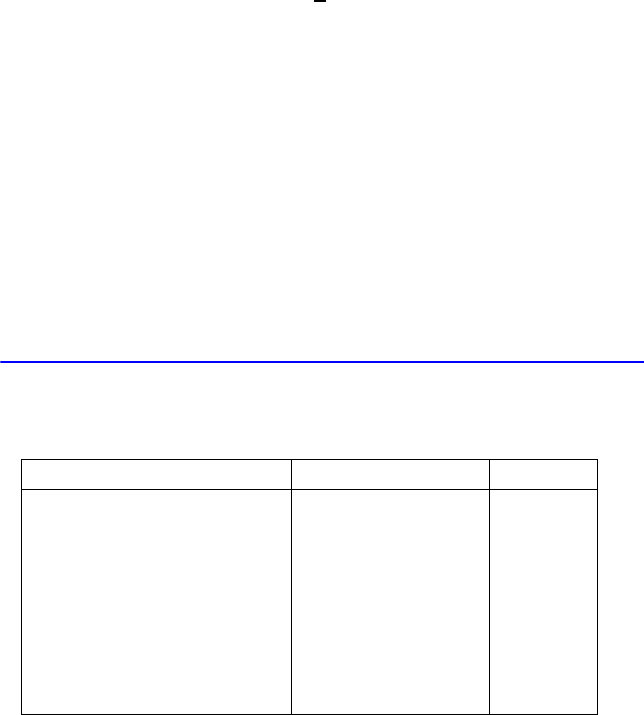
ALG: Samenvatting C-5
Voert u in py, dan berekent de rekenmachine
het resultaat, -107,6471. Dat is niet wat u wilt. De deling moet worden uitgesteld tot
u 85-12 hebt berekend, en daarvoor gebruikt u haakjes:
Voor een linker haakje kunt u het vermenigvuldingsteken (×) weglaten. Impliciete
vermenigvuldig is in de vergelijkingstand niet beschikbaar. Bijvoorbeeld, de
expressie 2 × (5 – 4) kan worden ingevoerd als 4, zonder dat u
op y drukt tussen de 2 en het linker haakje.
Exponentiële en logarithmische functies
Invoer: Weergave: Omschrijving:
p4 ,1.2 Er wordt niet gerekend.
Õ,1.2_Berekent 85 − 12.
y ,1.2º_Berekent 30/73.
,1.2º
)
Berekent 30/(85 − 12) ×
9.
Om te berekenen: Drukt u op: Weergave:
Natuurlijke logaritme (grondtal
e)
{- 12
)
Gewone logaritme (grondtal
10)
z+
12
)
Natuurlijke exponent {* %12
)
Gewone exponent (anti-
logaritme)
z( 12
)
ALG: Samenvatting C-7
Delen van getallen
De stapel bekijken
De toets 9 of {8 toont een menu op het scherm — registers X, Y, Z, T,
waarmee u de volledige inhoud van de stapel kunt bekijken. Het verschil tussen 9
en { 8 is de locatie van de onderstreping in het scherm. Met { 8 komt de
onderstreping in het T-register, en met 9 komt de onderstreping in het Y-register.
Met 9 verschijnt het volgende menu:
% & ' !
waarde
Met { 8 verschijnt het volgende menu:
% & ' !
waarde
U kunt op 9 en { 8 drukken (samen met Õ of Ö) om de gehele inhoud
van de stapel te bekijken en het op te roepen. Ze zullen verschijnen als %,
&, ' of ! afhankelijk van welk deel van de stapel was opgeroepen en
wordt misschien gebruikt in verdere berekeningen.
Om te berekenen: Drukt u op: Weergave:
Het gehele deel van 2,47 zJ()
1)2
)
Het gebroken deel van 2,47 zJ()
1)2
)
De absolute waarde van –7 { A_ 1.2
)
Het teken van 9 zJ( )
12
)
Het grootste gehele getal dat
niet meer is dan –5,3
zJ(!)_
!1.)2
.)

C-8 ALG: Samenvatting
De waarde van X-, Y-, Z-, T- register in de ALG stand is hetzelfde als die in de RPN
stand. Na normaal rekenen, oplossen, programmeren, of integreren, zal de waarde
van de vier registers hetzelfde zijn als in de RPN of ALG stand en bewaard blijven
als u verandert tussen ALG en RPN logische standen.
Een vergelijking integreren
1. Voer een vergelijking in (zie “Vergelijkingen aan de lijst van vergelijkingen
toevoegen” in hoofdstuk 6) en verlaat de vergelijkingenstand.
2. Voer de grenzen van de integratie in: toets in de onder grens en druk op
Z, toets dan de bovenste grens in.
3. Geef de vergelijking weer: Druk op G en, als het nodig is, scroll door de
vergelijkingenlijst (druk × of Ø) om de gewenste vergelijking weer te
geven.
4. Selecteer de variabele waarnaar geïntegreerd moet worden: Druk op z )
variabele. Nu begint de berekening.
Bewerkingen met complexe getallen
Een complex getal invoeren:
Vorm: º¸
1. Typ het reële deel in.
2. Druk op 6.
3. Typ het imaginaire deel in.
Vorm: º-¸
1. Typ het reële deel in.
2. Druk op .
3. Typ het imaginaire deel in.
4. Druk op 6.
Vorm: T
1. Typ de waarde van r in.
2. Druk op {?.

ALG: Samenvatting C-9
3. Typ de waarde van
θ
in.
Een bewerking maken met een complex getal:
1. Selecteer de functie.
2. Geef het complexe getal z op.
3. Druk op voor de berekening.
4. Het berekende resultaat wordt weergegeven in regel 2 en de weergegeven
vorm zal diegene zijn die u in 9 heeft ingesteld.
Een berekening maken met twee complexe getallen:
1. Geef het eerste complexe getal, z1, op.
2. Selecteer de wiskundige bewerking.
3. Geef het eerste complexe getal, z2, op.
4. Druk op voor de berekening.
5. Het berekende resultaat wordt weergegeven in regel 2 en de weergegeven
vorm zal diegene zijn die u in 9 heeft ingesteld.
Hier zijn een paar voorbeelden met complexe getallen:
Voorbeelden:
Evalueer sin (2+3i)
Voorbeelden:
Evalueer de expressie
z 1 ÷ (z2 + z3),
waarin z1 = 23 + 13 i, z2 = –2 + i z3 = 4 –3 i
Invoer: Weergave: Omschrijving:
z8 (º ¸)Weergavevorm instellen
N6 1- 2
1-L2
) .)
Resultaat is
9,1545 i–4,1689

C-10 ALG: Samenvatting
Voorbeelden:
Evalueer (4 - 2/5 i)×(3 - 2/3 i)
Rekenen met talstelsels 2, 8 en 16
Hier zijn een paar voorbeelden van berekeningen in Hexadecimaal, Octaal en
Binaire standen:
Voorbeeld:
12F16 + E9A16 = ?
Invoer: Weergave: Omschrijving:
z8Ë
(º-¸ )
Weergavevorm instellen
4
6
Õp4 _
66
§ª1.- -. 2
1- 2ª1.-)))
)-)
Resultaat is
2,5000 + 9,0000 i
Invoer: Weergave: Omschrijving:
4
6Õy4
6
§L2º1. + 2
1. + 2º1)))
) .)
Resultaat is
11,7333 i–3,8667
Invoer: Weergave: Omschrijving:
{w(%)Kiest hexadecimaal 16; de
annunciator HEX
verschijnt.

ALG: Samenvatting C-11
77608 – 43268=?
1008 ÷ 58=?
5A016 + 100110002 =?
Statistische gegevens met twee variabelen invoeren
Denk eraan dat u met ALG een paar van (x, y) in de omgekeerde volgorde (y
Z x of y x) moet invoeren, zodat y in het Y-register komt en X in het X-
register.
1. Druk op { (4Σ) om de vorige statistische gegevens te wissen.
2. Geef eerst de y-waarde op en druk op Z.
KF{
w(K)K
E9KA{
w(K)
K-K
K
Resultaat.
{w(!)K-K
µ
Kiest octaal 8: de
annunciator OCT
verschijnt.
{w
(µ)
{
w(µ)
µ.µ
µ
Converteert weergegeven
getal naar octaal.
{w
(µ) p{
w(µ)
µªµ
µ
Het gehele deel van het
resultaat.
{ w(%)
KA0{
w(K)
K- Kiest hexadecimaal 16;
de annunciator HEX
verschijnt.
{w(E)
§K-E
5A0h+10011000b
K
Resultaat in
hexadecimaal.
{w()K-EE
8)
Herstelt de decimaal.

C-12 ALG: Samenvatting
3. Geef de overeenstemmende x-waarde op en druk op 6.
4. Op het scherm staat n het aantal paren statistische gegevens dat u hebt
opgegeven.
5. Ga door met het invoeren van x,y-paren, n wordt opgewaardeerd met elke
invoer.
Als u de onjuiste waarden wilt wissen die net zijn ingevoerd, druk dan op z 4
. Na het wissen van de onjuiste statitische gegevens, zal de rekenmachine de
laatste statitische gegevens die in regel 1 zijn ingevoerd weergeven (bovenlijn van
het scherm) en waarde van n in regel 2. Als er geen statitische gegevens zijn, zal
de rekenmachine n=0 in regel 2 weergeven.
Voorbeeld:
Na het intoetsen van de x, y waarden aan de linkerkant, worden de correcties aan
de rechterkant getoond:
Initiaal x,y Gecorrigeerde x, y
20, 4 20, 5
400, 6 40, 6
Invoer: Weergave: Omschrijving:
{ (4Σ)Wist de bestaande statistische
gegevens.
Z6 Σ-
)
Voert het eerste nieuwe
gegevenspaar in.
Z
6
Σ-
)
Scherm toont n, het aantal paren dat
u heeft ingevoerd.
{ !º
)
Haalt de laatste x-waarde terug. De
laatste y is nog in het Y-register.
z 4 Σ.
)
Verwijdert het laatste paar.
Z6 Σ-
)
Geeft het laatste paar opnieuw op.
Zz
4
Σ.
)
Verwijdert het eerste paar.
Z6 Σ-
)
Geeft het eerste paar opnieuw op.
Er staan nog steeds twee paren in
de statistische registers.
ALG: Samenvatting C-13
Lineaire regressie
Lineaire regressie, of L.R. (ook genoemd lineaire schatting) is een statistische
methode om een rechte lijn te vinden die het best overeenkomt met een reeks x, y-
gegevens.
Om een geschatte waarde te vinden voor x (of y), geeft u een hypothetische
waarde op voor y (of x), druk op en druk dan op z , () (of
z ,Õ ()).
Om de waarden te vinden die het best overeenkomen met de lijn die door uw
gegevens loopt, drukt u op z , gevolgd door (T), (P), of (E).
º
ˆ
¸
ˆ

Meer over het oplossen met SOLVE D-1
D
Meer over het oplossen met SOLVE
Dit aanhangsel geeft informatie over de SOLVE-bewerking. Het is een uitbreiding
van hoofdstuk 7.
Hoe SOLVE een wortel vindt
SOLVE probeert eerst de vergelijking direct voor de onbekende variabele op te
lossen. Lukt dat niet, dan doet SOLVE het met een iteratieve (herhaalde) procedure.
De iteratieve bewerking voert de vergelijking meermalen uit. De teruggegeven
waarde is een functie f(x) van de onbekende variabele x. (f(x) is een wiskundige
notatie voor een functie die gedefinieerd is in termen van de onbekende variabele
x.) SOLVE start met een schatting voor de onbekende variabele x, en verfijnt die
schatting met iedere volgende executie van de functie f(x).
Hebben twee opeenvolgende evaluaties van de functie f(x) een tegengesteld teken,
dan veronderstelt SOLVE dat de functie f(x) daartussen minstens een keer de x-as
kruist. Het interval wordt verder vernauwd tot er een wortel wordt gevonden.
Om met SOLVE een wortel te kunnen vinden, is het wel nodig dat de wortel bestaat
binnen het bereik van de rekenmachine, en de functie moet wiskundig gdefinieerd
zijn op de plaats waar iteratief wordt gezocht. SOLVE vindt altjid een wortel, mits
die bestaat (binnen de grenzen van overflow), als er aan een of meer van de
volgende condities is voldaan:
Twee schattingen geven functiewaarden f(x) met een tegengesteld teken, en
de functie kruist de x-as op minstens een plaats tussen die schattingen
(afbeelding a, hieronder).
f(x) is monotoon: de functiewaarde stijgt of daalt altijd als x stijgt (afbeelding
b, hieronder).
De grafiek van f(x) is overal concaaf of overal convex (afbeelding c,
hieronder).
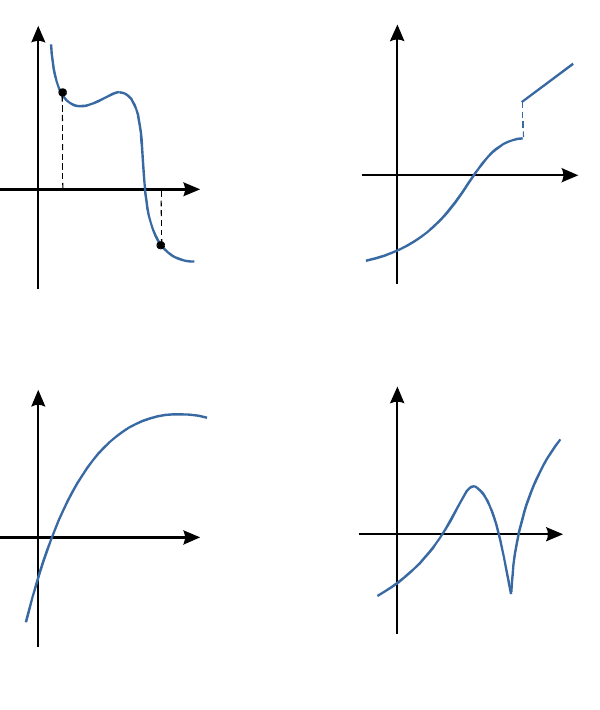
D-2 Meer over het oplossen met SOLVE
Als f(x) een of meer lokale minima of maxima heeft, bevindt ieder zich tussen
twee opeenvolgende wortels van f(x) (afbeelding d, hieronder).
In de meeste situaties is de berekende wortel een nauwkeurige schatting van de
theoretische, oneindig nauwkeurige wortel van de vergelijking. Een “ideale”
oplossing is een oplossing waarbij f(x) = 0. Een zeer kleine waarde van f(x) is vaak
acceptabel omdat die kan voortvloeien uit de benadering met een precisie van 12
cijfers.
f (x)
x
a
f (x)
b
x
f (x)
x
c
f (x)
x
d
Functies waarvan de wortel
g
evonden kan worden

Meer over het oplossen met SOLVE D-3
Resultaten interpreteren
De SOLVE-bewerking geeft een oplossing onder één van de volgende
voorwaarden:
Indien er een schatting wordt gevonden waarvoor f(x) gelijk is aan nul. (Zie
afbeelding a, hieronder.)
Indien er een schatting wordt gevonden waarvoor f(x) niet gelijk is aan nul,
maar de berekende wortel een getal is van 12 cijfers nabij het punt waar de
grafiek van de functie de x-as kruist (zie afbeelding b, hieronder). Dat is het
geval als de twee schattingen buren zijn (d.w.z. ze verschillen 1 in het
twaalfde cijfer) en de functiewaarde positief is voor de ene schatting en
negatief voor de andere. Of ze zijn (0, 10–499) of (0, –10–499). In de
meeste gevallen zal f(x) relatief dicht bij nul zijn.
Voor extra informatie over het resultaat, drukt u op 9 om de vorige schatting van
de wortel (x) te zien, die zich nog in het Y-register bevindt. Druk opnieuw op 9
om de waarde van f(x) te zien, die zich in het Z-register bevindt. Is f(x) gelijk aan
nul of relatief klein, dan is het waarschijnlijk dat er een oplossing is gevonden. Is
f(x) relatief groot, wees dan voorzichtig bij het interpreteren van de resultaten.
Voorbeeld: Een vergelijking met één wortel.
Bepaal de wortel van de vergelijking:
–2x3 + 4x2 – 6x + 8 = 0
Voer de vergelijking in als een expressie:
D-4 Meer over het oplossen met SOLVE
Los nu de vergelijking op om de wortel te vinden:
Voorbeeld: Een vergelijking met twee wortels.
Bepaal de twee wortels van de parabolische vergelijking:
x2 + x – 6 = 0.
Voer de vergelijking in als een expressie:
Invoer: Weergave: Omschrijving:
GSelecteert de
vergelijkingenstand.
_y
KX0
y
KX0
yKX
.º%:-º%:.¨
Voert de vergelijking in.
z /
/
Controlesom en lengte.
Beëindigt vergelijkingenstand.
Invoer: Weergave: Omschrijving:
{HX
_Beginwaarden voor de wortel.
G.º%:-º%:.¨
Selecteert de vergelijkingenstand;
geeft het linkerdeel van de
vergelijking weer.
{X #
%/
)
Lost X op en toont het resultaat.
9) Laatste twee schattingen zijn
hetzelfde in vier decimalen.
9.). f(x) is zeer klein, dus de
benadering is een goede
wortel.
Meer over het oplossen met SOLVE D-5
Los nu de vergelijking op om de positieve en negatieve wortel te vinden:
Bij sommige gevallen is nog wat denkwerk nodig:
Als de grafieksfunctie een discontinuïteit heeft die de x- as kruist, keert de
SOLVE bewerking een aangrenzende waarde terug naar de discontinuïteit
(zie figuur a, hieronder). In dit geval, kan f(x) relatief hoog zijn.
Invoer: Weergave: Omschrijving:
GSelecteert de vergelijkingenstand.
KX0
KX
%:-%.
Voert de vergelijking in.
z /
/
Controlesom en lengte.
Beëindigt vergelijkingenstand.
Invoer: Weergave: Omschrijving:
{HX
_Beginwaarden voor de positieve
wortel.
G%:-%. Selecteert de vergelijkingenstand;
geeft van de vergelijking weer.
{X #
%/
)
Berekent de positieve wortel met
beginwaarden 0 en 10.
9) Laatste twee schattingen zijn
hetzelfde.
9z ) f(x) = 0.
{HX
_
._Beginwaarden voor de negatieve
wortel.
G%:-%. Geeft de vergelijking opnieuw
weer.
{X #
%/
.)
Berekent de negatieve wortel met
beginwaarden 0 an –10.
9 9z ) f(x) = 0.

D-6 Meer over het oplossen met SOLVE
Waarden van f(x) kunnen naderen tot oneindig op de plaats waar het teken
van de functie verandert (zie afbeelding b, hieronder). Deze situatie heet een
paal. Doordat SOLVE vaststelt dat het teken verandert tussen twee
opeenvolgende waarden van x, veronderstelt hij dat zich hier een wortel
bevindt. De waarde van f(x) is echter relatief hoog. Bevindt de paal zich bij
een waarde van x die precies met 12 cijfers gerepresenteerd kan worden,
dan zal de berekening bij die waarde vastlopen met een foutmelding.
Voorbeeld: Een discontinuïteitsfunctie
Bepaal de wortel van de vergelijking:
IP(x) = 1,5
Voert de vergelijking in:
Invoer: Weergave: Omschrijving:
GSelecteert de
vergelijkingenstand.
zJ()
KXÕzc
1%2/)
Voert de vergelijking in.
z /
/
Controlesom en lengte.
Beëindigt vergelijkingenstand.
f (x)
x
a
f (x)
x
b
Special geval: een discontinuïteit en een paal

Meer over het oplossen met SOLVE D-7
Nu oplossen om de wortel te vinden:
Let op het verschi tussen de laatste twee schattingen, en op de hoge waarde van
f(x). Het probleem is dat er geen waarde van x is waarbij f(x) = 0. Bij x =
1,99999999999 is er echter een waarde in de directe omgeving x waarbij de
functiewaarde het omgekeerde teken is voor f(x).
Voorbeeld:
Bepaal de wortel van de vergelijking
Nader x tot , dan wordt f(x) een zeer groot positief of negatief getal.
Voer de vergelijking in als een expressie.
Invoer: Weergave: Omschrijving:
{HX
_Uw beginwaarden voor de wortel.
G1%2/) Selecteert de vergelijkingenstand;
geeft van de vergelijking weer.
{X #
%/
)
Zoekt een wortel met
beginwaarden 0 en 5.
z ) Geeft de wortel met 11 decimalen
weer.
9z ) De vorige schatting is iets groter.
9.) f (x) is relatief hoog
Invoer: Weergave: Omschrijving:
GSelecteert de
vergelijkingenstand.
01
6
2=−
−x
x
6

D-8 Meer over het oplossen met SOLVE
Nu oplossen om de wortel te vinden.
Als SOLVE geen wortel kan vinden
Soms kan SOLVE geen wortel vinden. De volgende condities resulteren in de
melding ! :
De zoektocht sluit af vlabij een lokaal minimum of maximum (zie figuur a,
hieronder).
De zoektocht eindigt omdat SOLVE werkt met een horizontale asymptoot—
waarin f(x) vrijwel constant is voor een groot bereik van x (zie afbeelding b,
hieronder).
De zoektocht is geconcentreerd in een lokaal “vlak” interval van de functie
(zie afbeelding c, hieronder).
In deze gevallen, zullen de waarden in de stapel hetzelfde zijn als de waarden
voordat SOLVE uitgevoerd wordt.
KXp4
KX0
Õ
%ª1%:.2.
Voert de vergelijking in.
z /
/
Controlesom en lengte.
Beëindigt vergelijkingenstand.
Invoer: Weergave: Omschrijving:
{
HX
)_
Uw beginwaarden voor de
wortel.
G%ª1%:.2. Selecteert de
vergelijkingenstand; geeft van
de vergelijking weer.
{X ! Geen wortel gevonden voor
f(x).

Meer over het oplossen met SOLVE D-9
Voorbeeld: Een relatief minimum.
Bereken de wortel van deze parabolische vergelijking:
x2 – 6x + 13 = 0.
Hij heeft een minimum bij x = 3.
Voer de vergelijking in als een expressie:
Invoer: Weergave: Omschrijving:
GSelecteert de vergelijkingenstand.
KX0
yKX
%:.º%-
Voert de vergelijking in.
f
(
x
)
x
a
f
(x)
x
b
f (x)
x
c
Geval waarin geen wortel gevonden is

D-10 Meer over het oplossen met SOLVE
Nu oplossen om de wortel te vinden:
Voorbeeld: Een asymptoot.
Bepaal de wortel van de vergelijking
Voer de vergelijking in als een expressie.
z /
/
Controlesom en lengte.
Beëindigt vergelijkingenstand.
Invoer: Weergave: Omschrijving:
{HX
_
Uw beginwaarden voor de wortel.
G%:.º%- Selecteert de vergelijkingenstand;
geeft van de vergelijking weer.
{X ! De zoektocht faalt met
beginwaarden 0 en 10
Invoer: Weergave: Omschrijving:
GSelecteert de vergelijkingenstand.
3
KX.#1%2
Voert de vergelijking in.
z /
/
Controlesom en lengte.
Beëindigt vergelijkingenstand.
{
HX _
Uw positieve beginwaarden voor
de wortel.
G.#1%2 Selecteert de vergelijkingenstand;
geeft van de vergelijking weer.
{X%/
)
Lost x op met beginwaarden
0,005 en 5.
9) Vorige schatting was dezelfde.
9z ) f (x) = 0
0
1
10 =− X

Meer over het oplossen met SOLVE D-11
Dit gebeurt er als u negatieve beginwaarden gebruikt:
Voorbeeld: Een rekenfout.
Voer de vergelijking in als een expressie:
Probeer eerst een positieve wortel te vinden:
Invoer: Weergave: Omschrijving:
_{HX
.) Uw negatieve beginwaarden voor
de wortel.
_G .#1%2 Selecteert de vergelijkingenstand;
geeft van de vergelijking weer.
{X%/
)
Lost X op en toont het resultaat.
Invoer: Weergave: Omschrijving:
GSelecteert de
vergelijkingenstand.
<KXp4
KX
ÕÕ
!1%ª1%-)22¨
Voert de vergelijking in.
z /
/
Controlesom en lengte.
Beëindigt
vergelijkingenstand.
Invoer: Weergave: Omschrijving:
{HX
_
Uw positieve beginwaarden
voor de wortel.
G !1%ª1%-)22¨Selecteert de
vergelijkingenstand; geeft het
linkerdeel van de vergelijking
weer.
{X%/
)
Berekent de wortel met
beginwaarden 0 en 10
D-12 Meer over het oplossen met SOLVE
Probeer nu een negatieve wortel te vinden met de beginwaarden 0 en –10. Merk
op dat de functie ongedefinieerd is voor waarden van x tussen 0 en –0,3 omdat die
waarden een positieve noemer geven maar een negatieve teller, zodat de wortel
moet worden getrokken van een negatief getal.
Voorbeeld: een lokaal “vlak” interval.
Bepaal de wortel van de functie
f(x) = x + 2 if x < –1,
f(x) = 1 voor –1 ≤ x ≤ 1 (een lokaal vlak interval),
f(x) = –x + 2 if x >1.
In de RPN-stand, voer de functie in als een programma:
- %
º6¸@
!
.
-+.
º5¸@
¶
!
Controlesom en lengte: 9412 39
Invoer: Weergave: Omschrijving:
{HX
_ ._
G !1%ª1%-)22¨Selecteert de
vergelijkingenstand; geeft het
linkerdeel van de vergelijking
weer.
{X ! Geen wortel gevonden voor
f(x).

Meer over het oplossen met SOLVE D-13
Los X op met beginwaarden 10–8 en –10–8.
Afrondfouten
De beperkte precisie (12-cijfers) van de rekenmachine kan afrondfouten
veroorzaken, die de iteratieve oplossingen van SOLVE en integratie nadelig kunnen
beïnvloeden. Bijvoorbeeld,
heeft geen wortels omdat f(x) is altijd groter is dan nul. Echter, met beginwaarden 1
en 2 zal SOLVE de waarde 1,0000 geven door een afrondfout.
Afrondfouten kunnen ook tot gevolg hebben dat SOLVE geen wortel vindt. De
Vergelijking
heeft een wortel bij . Er is echter geen getal van 12 cijfers dat precies gelijk is
aan , dus de rekenmachine slaagt er niet in de functiewaarde nul te maken.
Verder verandert het teken van de functie nooit. SOLVE geeft dan ook de melding
! .
Invoer:
(In de RPN-stand)
Weergave: Omschrijving:
`
_{HX
_ ` _
.._
Geeft beginwaarden op.
zVJ.). Selecteert programma “J” als de
functie.
{X%/
.)
Lost X op en toont het resultaat.
0 10 - ]10 1) x [( 30215 =++
0 7-x2=
7
7

Meer over integratie E-1
E
Meer over integratie
Dit aanhangsel geeft achtergrondinformatie over integratie. Het is een uitbreiding
van hoofdstuk 8.
Hoe de integraal geëvalueerd wordt
Het algoritme dat wordt gebruikt voor integraties, ∫ Gº, berekent de integraal
van een functie f(x) door een gewogen gemiddelde te bepalen van de
functiewaarden bij een groot aantal waarden van x (monsterpunten) binnen het
integratie-interval. De nauwkeurigheid van een dergelijke integratie is afhankelijk
van het aantal monsterpunten. Over het algemeen geldt, hoe meer monsterpunten,
hoe nauwkeuriger. Zouden we f(x) bij een oneindig aantal monsterpunten
evalueren, dan zou het algoritme — afgezien van de onnauwkeurigheid bij het
berekenen van de functiewaarde f(x) — altijd een exact antwoord geven.
Natuurlijk zou het algoritme eeuwig duren als er bij een oneindig aantal
monsterpunten werd geëvalueerd. Dit is echter ook niet nodig, omdat de
nauwkeurigheid toch al beperkt wordt door de nauwkeurigheid van de berekende
functiewaarden. Door een eindig aantal monsterpunten te gebruiken, kan het
algoritme een integraal berekenen die zo nauwkeurig als gerechtvaardigd is, als
we rekening houden met de onnauwkeurigheid in f(x).
Het integratie-algoritme bekijkt eerst een aantal monsterpunten, die een relatief
onnauwkeurige benadering geven. Is deze benadering nog niet zo nauwkeurig als
de nauwkeurigheid van f(x) toestaat, dan wordt het algoritme geïtereerd (herhaald)
met een groter aantal monsterpunten. Zo gaat het verder, waarbij er steeds twee
keer zoveel monsterpunten worden genomen, tot het resultaat na het resultaat zo
nauwkeurig als gerechtvaardig is met betrekking tot de inherente onnauwkeurigheid
in f(x).

E-2 Meer over integratie
In hoofdstuk 8 legden we al uit dat de onzekerheid van de uiteindelijke benadering
wordt afgeleid van de decimalen die in de weergave zijn ingesteld. Aan het einde
van iedere iteratie vergelijkt het algoritme de berekende benadering met de
benadering van de twee vorige iteraties. Is het verschil tussen één van deze
benaderingen en de andere twee minder dan de onzekerheid die geoorloofd is in
het eindresultaat, dan eindigt de berekening. De huidige benadering komt in het X-
register en de onzekerheid in het Y-register.
Het is uiterst onwaarschijnlijk dat de fouten in de drie opeenvolgende
benaderingen— dat wil zeggen, de verschillen tussen de werkelijke integraal en de
benaderingen— groter zijn dan de verschillen tussen de benaderingen zelf. De fout
in de uiteindelijke benadering is dus minder dan de onzekerheid (mits f(x) niet zeer
snel varieert). Hoewel we de fout in de uiteindelijke benadering niet kunnen weten,
is het uiterst onwaarschijnlijk dat die fout groter is dan de weergegeven
onzekerheid in de benadering. Met andere woorden, de schatting van de
onzekerheid in het Y-register is vrijwel zeker een “bovengrens” van het verschil
tussen de benadering en de werkelijke integraal.
Voorwaarden waaronder er onjuiste resultaten
ontstaan
Hoewel het integratie-algorithme in de HP 35s één van de beste is, zijn er situaties
waarin het — zoals alle algoritmen voor numerieke integratie — een onjuist
antwoord oplevert. De kans dat dit gebeurt is uiterst gering. Het algoritme is
ontworpen om nauwkeurige resultaten te geven met bijna iedere continue functie.
Alleen voor functies die zich uiterst onregelmatig gedragen is er een zekere kans
dat u een onnauwkeurig antwoord krijgt. Zulke functies komen zelden voor in
problemen die verband houden met een werkelijke fysieke situatie, en als ze
voorkomen, zult u ze meestal herkennen, zodat u weet dat ze beter op een andere
manier geïntegreerd kunnen worden.
Helaas weet het algoritme niets meer van f(x) dan de functiewaarden bij de
monsterpunten. Het kan geen onderscheid maken tussen f(x) en een andere functie
die op de monsterpunten dezelfde functiewaarden heeft. Deze situatie is hieronder
geïllustreerd, met (over een deel van het integratie-interval) drie functies waarvan de
grafieken veel monsterpunten gemeen hebben.

Meer over integratie E-3
Met dit aantal monsterpunten vindt het algoritme dezelfde benadering voor de
integraal voor elk van de drie weergegeven functies. De ware integralen van de
functies met de doorgetrokken zwarte en blauwe lijnen zullen niet zo veel
verschillen, zodat de benadering redelijk nauwkeurig is als f(x) een van deze
functies is. Echter, de ware integraal van de gestreepte lijn is heel anders. De
gevonden benadering is dus niet nauwkeurig als f(x) deze functie is.
Het algoritme bepaalt het algemene gedrag van de functie door de functie op
steeds meer punten te bemonsteren. Lijkt de fluctuatie van de functie in het ene
interval veel op het gedrag in de rest van het integratie-interval, dan zal het
algoritme die fluctuatie waarschijnlijk wel ontdekken. Gebeurt dat, dan wordt het
aantal monsterpunten verhoogd tot opeenvolgende iteraties benaderingen
opleveren die rekening houden met de snelste, maar kenmerkende, fluctuaties.
Bijvoorbeeld, neem de benadering van
Omdat u deze integraal numeriek evalueert, zou u kunnen denken dat u als
bovenlimiet 10499 moet opgeven, het hoogste getal dat u in de rekenmachine kunt
invoeren.
f (x)
x
.
0
∫∞−dxxe x

Meer over integratie E-5
De grafiek is een impuls die zeer dicht bij de oorsprong ligt. Helaas was er geen
monsterpunt om die impuls te ontdekken en het algoritme veronderstelde dat f(x)
gelijk was aan nul over het hele integratie-interval. Zelfs als u het aantal
monsterpunten verhoogt door de integraal met SCI 11 of ALL te berekenen, zal
geen van de monsterpunten de impuls ontdekken als deze functie over het gegeven
interval geïntegreerd wordt. (Voor een betere aanpak van dergelijke problemen,
verwijzen we naar “Condities die de rekentijd verlengen” hieronder.)
Zulke functies (met een fluctuatie die je niet zou verwachten als je het gedrag van
een ander deel van de functie zag) zijn gelukkig zo ongebruikelijk dat het niet
waarschijnlijk is dat u er ooit een zult integreren. Een functie die onjuiste resultaten
kan opleveren kan geïdentificeerd worden door de snelheid waar de functie en de
eerst afgeleiden variëren rondom het integratie-interval. Hoe sneller de functie
varieert in de afgeleiden, en vooral als dat in de eerste paar afgeleiden gebeurt,
hoe trager de berekening zal verlopen, en hoe minder betrouwbaar het resultaat
uiteindelijk is.
f (x)
x

E-6 Meer over integratie
Merk op dat de snelheid van de variatie in de functie (van de eerste paar
afgeleiden) beschouwd moet worden binnen het integratie-interval. Met een
gegeven aantal monsterpunten, kan een functie f(x) die drie fluctuaties heeft beter
gekarakteriseerd worden met de monsters als die variaties zijn uitgespreid over de
breedte van het integratie-interval dan wanneer ze beperkt zijn tot een klein deel
van het interval. (Deze twee situaties zijn afgebeeld in de volgende twee
illustraties.) Beschouwen we de variaties als een soort oscillatie in de functie, dan
gaat het om de verhouding tussen de periode van de trillingen en de breedte van
het integratie-interval: hoe groter deze verhouding, hoe sneller de berekening
voltooid is, en hoe betrouwbaarder de resulterende benadering.
f (x)
x
Calculated integral
of this function
will be accurate.
f (x)
a b
x
Calculated integral
of this function
may be inaccurate.
a b
De berekende integral
van deze functie is
naukeuring.
DE berekende integral van
deze functie kan
onnauwkeurig zijn.

Meer over integratie E-7
In veel gevallen zult u wel bekend zijn met de functie die u wilt integreren, zodat u
wel weet of er vreemde fluctuaties zijn binnen het integratie-interval. Bent u niet
bekend met de functie, en vreest u problemen, dan kunt u snel een grafiek tekenen
door de functie te evalueren met de vergelijking of het programma dat u daarvoor
hebt geschreven.
Als u, om welke reden dan ook, na het berekenen van een integraal, twijfelt aan de
juistheid ervan, dan is er een eenvoudige manier om deze te controleren: verdeel
het integratie-interval in twee of meer aaneengesloten subintervallen, integreer de
functie over ieder subinterval, en tel de resultaten op. Hierdoor wordt de functie
bemonsterd op een geheel andere reeks monsterpunten, waardoor wellicht
verborgen onregelmatigheden aan het licht komen. Is de oorspronkelijke
benadering juist, dan zal hij gelijk zijn aan de som van de benaderingen over
subintervallen.
Condities die de rekentijd verlengen
In het vorige voorbeeld gaf het algoritme een onjuist antwoord doordat de impuls in
de functie niet werk opgemerkt. Dat kwam doordat de impuls zo smal was ten
opzichte van de breedte van het integratie-interval. Was het interval smaller, dan
zou u het juiste antwoord hebben gekregen, maar dat zou ook langer geduurd
hebben als het interval nog steeds te breed was.
Neem een integraal waarvan het integratie-interval breed genoeg is om veel tijd
nodig te hebben, maar niet zo breed dat de berekening onjuist zal zijn. Doordat
f(x) = xe–x snel tot nul nadert als x nadert tot ∞, draagt de functiewaarde bij hoge
waarden van x weinig bij aan de waarde van de integraal. Het is dus voldoende
om de integraal te evalueren door ∞, de bovengrens van het interval, te vervangen
door een lager getal, niet door 10499 — maar bijvoorbeeld 103.
Herhaal het vorige integratieprobleem met de nieuwe bovengrens:
Invoer: Weergave: Omschrijving:
`
_Nieuwe bovengrens.
G%º%1.%2 Selecteert de vergelijkingenstand;
geeft van de vergelijking weer.

E-8 Meer over integratie
Dit is het juiste antwoord, maar het duurde erg lang. Om dat te begrijpen,
vergelijken we de grafiek van de functie tussen x = 0 en x = 103, die er ongeveer
net zo uitziet als in het vorige voorbeeld, met de grafiek van de functie tussen x = 0
en x = 10:
U ziet dat de functie eigenlijk alleen bij kleine waarden van x “interessant”. Bij
grotere waarden van x, is de functie niet van belang, want hij nadert steeds dichter
tot nul.
Het algoritme bemonstert de functie met een grotere dichtheid van monsterpunten
totdat het verschil tussen twee opeenvolgende benaderingen voldoende klein is.
Binnen een klein interval in een gebied waar de functie interessant is, kost het
minder tijd om de kritieke dichtheid te bereiken.
Om dezelfde dichtheid van monsterpunten te bereiken, zijn er over een groot
interval veel meer monsterpunten nodig dan over een klein interval. Dus waren er
veel meer iteraties nodig over het grotere interval om een benadering te krijgen met
dezelfde nauwkeurigheid, en dus kostte de berekening van de integraal veel meer
tijd.
z)X!!
∫ /
)
Integraal. (De berekening duurt
ongeveer twee minuten.)
Z). Onnauwkeurigheid van de
benadering.
x
f (x)
0 10
Meer over integratie E-9
Doordat de rekentijd afhangt van de snelheid waarmee een zekere dichtheid van
monsterpunten wordt bereikt in het gebied waarin de functie interessant is, duurt de
berekening van de integraal van een functie langer als het integratie-interval
voornamelijk gebieden bevat waarin weinig interessants gebeurt. Als u zo’n
integraal moet berekenen, dan kunt het probleem gelukkig veranderen, zodat de
rekentijd aanmerkelijk verminderd wordt. Twee van zulke technieken zijn het
onderverdelen van het integratie-interval en transformatie van variabelen. Met deze
methoden kunt u de functie of de integratiegrenzen veranderen zodat de integrand
zich beter gedraagt binnen het integratie-interval.

Berichten F-1
F
Berichten
De rekenmachine reageert op sommige condities door een melding te tonen. Het
symbool £ geeft aan dat uw aandacht vereist. Bij een significante conditie blijft de
melding staan tot u hem verwijdert. Met de toets of a verwijdert u het
bericht; met een willekeurige andere toets wordt het bericht verwijderd en de functie
van die toets uitgevoerd.
∫ !# A running program attempted to select a program label
(/label) while an integration calculation was running.
∫ 1∫ 2 Een lopend programma probeerde een programma te
integreren (∫ G variabele) terwijl er een andere
integratie actief was.
∫ 1 #2 Een lopend programma probeerde een programma op
te lossen terwijl er een integratie actief was.
# / De catalogus van variabelen ( z X (#) )
geeft aan dat er geen waarden zijn opgeslagen.
" U heeft een verkeerd begingetal ingevoerd ( zoals een
complex getal of vector) wannneer een vergelijking voor
een variabele wordt OPGELOST.
"! De rekenmachine voert een functie uit die enige tijd kan
duren.
@ & Hiermee bevestigt u dat u alles uit het geheugen wilt
verwijderen.
@ & Hiermee kunt u een vergelijking verwijderen die u aan
het bewerken bent. (Treedt alleen op in de
vergelijkingenstand.)
@ & Hiermee bevestigt u dat u alle programma’s uit het
geheugen wilt verwijderen. (Treedt alleen op bij
programmainvoer.)
# & Poging te delen door nul. (Ook bij zS als het
Y-register nul bevat.)
F-2 Berichten
"!) Poging om een programmalabel op te geven dat al
bestaat in een andere programmaroutine.
! ! De “bovenkant” van het vergelijkingengeheugen. het
geheugenscherm is circulair, zodat ! ! ook
de “vergelijking” is na de laatste vergelijking in het
vergelijkingengeheugen.
!! De rekenmachine berekent de integraal van een
vergelijking of programma. Dit kan enige tijd duren.
!"! Een lopend CALCULATE SOLVE of ∫ FN programma was
gestoord door het drukken op of f in ALG, RPN,
EQN, of PGM mode.
# ! Gegevensfout:
Poging om foute gegevens op te slaan of te
berekenen.
Poging om combinaties of permutaties te berekenen
met r > n, met niet-gehele r of n, of met n ≥1016.
Poging om een complex getal of vecor in de
statistische gegevens op te slaan.
Poging om een basis-n getal dat cijfers groter dan
het grootste basis-n getal cijfer dat is toegestaan op
te slaan.
Poging om een onjuist gegeven in het statitische
register op te slaan met Z.
Poging om complexe getallen of vectoren te
vergelijken.
Poging om een trigonometrische of hyperbolische
functie te berekenen met een illegaal argument:
T als x een oneven meervoud is van 90°.
{O of {L met x < –1 of x > 1.
z7{ R met x ≤ –1; of x ≥ 1.
z7{O met x < 1.
# # Er werd geprobeerd een ongeldige variabele in te
voeren tijdens het oplossen van een vergelijking.
# º7 Er werd geprobeerd een faculteit of gamma operatie te
berekenen met een negatief geheel getal.
Berichten F-3
# ¸ºFout bij machtsverhefffen:
Nul in de macht nul of in een negatieve macht.
Een negatief getal in een gebroken macht.
Een complex getal (0 + i 0) in een macht met een
negatief reëel deel.
# 12Poging tot een bewerking met een onjuiste indirecte
waarde ((I) is niet bepaald).
# 12Poging tot een bewerking met een onjuiste indirecte
waarde ((J) is niet bepaald).
12 Logaritme van nul of van (0 + i0).
12 Logaritme van een negatief getal.
& Het gehele gebruikers geheugen is gewist (zie pagina
B–3).
& " De rekenmachine heeft onvoldoende geheugen om de
bewerking uit te voeren (Zie aanhangsel B).
De conditie die werd getest door een testinstructie is niet
waar. (Alleen indien uitgevoerd vanaf het toetsenbord.)
% !! Verwijzing naar een niet-bestaand programmalabel (of
regelnummer) met U,W, of . De melding
% !! kan betekenen
u hebt expliciet (met het toetsenbord) een
programmalabel opgeroepen dat niet bestaat; of
het programma dat u hebt aangeroepen refereerde
aan een ander label, dan niet bestaat.
Het resultaat van de integratie bestaat niet.
De catalogus van programma’s ( z X
() ) geeft aan dat er geen programmalabels zijn
opgeslagen.
"! Geen oplossing kon gevonden worden voor dit systeem
van liniaire vergelijkingen.
"! "! Verscheidene oplossingen zijn gevonden voor dit
systeem van liniaire vergelijkingen.
! SOLVE (inclusief EQN en PGM) kan de wortel van de
vergelijking niet vinden met gebruik van de huidige
beginwaarde (zie pagina D-8). Deze condities bevat:
slechte waarde, oplossing niet gevonden, punt van
interesse, links oneven naar rechts. Een SOLVE
bewerking uitgevoerd in een programma maakt deze
fout niet; dezelfde conditie laat het overslaan naar de
volgende programmaregel ( de regel die volgt na de
instructie # variabele).

Berichten F-5
Berichte van de zelftest:
!! Statistiekfout:
Statistische berekening met n = 0.
Berekening van sx sy, , , m, r, of b met n = 1.
Poging tot het berekenen van r, of met alleen
x- gegevens (alle y-waarden zijn gelijk aan nul).
Berekening van , , r, m, of b waarbij alle x-
waarden gelijk zijn.
&!% Een syntax fout was ontdekt tijdens de evaluatie van een
berekening, vergelijking,, of ". Het drukken
op aof wist de foutmelding en laat u de fout
verbeteren.
! Het getal is te groot om geconverteerd te worden naar
HEX, OCT of BIN; het getal moet liggen in het interval
–34.359.738.368 ≤ n ≤34.359.738.367.
% #$ Een lopend programma probeerde een eenentwintigste
geneste % label. (Maximaal 20 subroutines kunnen
genest worden). Aangezien SOLVE en ∫ FN elk een
niveau gebruiken, kunnen zij ook een fout genereren.
& De conditie, die is getest door een test-instructie, is waar.
(Alleen indien uitgevoerd vanaf het toetsenbord.)
. De zelftest en de test van het toetsenbord zijn
geslaagd.
. nDe zelftest of de test van het toetsenbord is
mislukt en de rekenmachine moet gerepareerd
worden.
© # ) ) ) Auteursrechtmelding verschijnt na een
succesvolle zelftest.
x
ˆy
ˆ
x
ˆwx
x
ˆy
ˆ

Index van bewerkingen G-1
G
Index van bewerkingen
In dit aanhangsel vindt u een snelle referentie van alle functies en bewerkingen en
hun formules, voorzover van toepassing. De listing is in alfabetische volgorde op
naam van de functie. Deze naam wordt gebruikt in programmaregels. Bijvoorbeeld,
de functie genaamd FIX n wordt uitgevoerd als z8 (1%) n.
Nite-programmeerbare functies zijn afgebeeld als toetsen. Bijvoorbeeld, a.
Griekse letters en tekens die geen letters zijn komen vóór de letters. Functienamen
die worden voorafgegaan door een pijl zijn gealfabetiseerd alsof de pijl er niet
was (bijvoorbeeld DEG).
De laatste kolom, met gemarkeerd , verwijst naar de voetnoten aan het einde.
Naam Toetsen en omschrijving Pagina
+/– _
Verandert het teken van een getal.
1–15 1
+ Optelling. Geeft y + x.1–19 1
– Aftrekking. Geeft y – x.1–19 1
×y Vermenigvuldiging. Geeft y × x.1–19 1
÷p Deling. Geeft y ÷ x.1–19 1
^0 Machtsverheffen. Geeft een
exponent.
6–16 1
aVerwijdert het laatste ingevoerde cijfer,
maakt x leeg; verwijdert een menu;
wist de laatste functie in een
vergelijking; verwijdert een
vergelijking; verwijdert een
programmastap.
1–4
1–8
6–3
13–7
×Gaat naar de vorige regel in de
catalogus; gaat naar de vorige
vergelijking in de vergelijkingenlijst;
gaat naar de vorige programmaregel.
1–28
6–3
13–11
13–20

G-2 Index van bewerkingen
ØGaat naar de volgende regel in de
catalogus; gaat naar de volgende
vergelijking in de vergelijkingenlijst;
gaat naar de volgende
programmaregel (tijdens
programmainvoer); voert de huidige
programmaregel uit (niet tijdens
programmainvoer).
1–28
6–3
13–11
13–20
Ö of ÕVerplaatst de cursor en verwijdert niets
uit de inhoud.
1–14
{Ö of {ÕSchuift het beeld zodat er links en
rechts meer cijfers worden getoond;
toont de rest van een vergelijking of
binair getal; gaat naar de volgende
menupagina van het menu CONST of
SUMS.
1–11
6–4
11–8
{×Gaat naar de bovenste regel van de
vergelijking of de eerste regel van de
laatste label in de programmastand.
6–3
{ØGaat naar de laatste regel van de
vergelijking of de eerste regel van de
laatste label in de programmastand.
6–3
,z Verdeelt de twee of drie
argumenten van een functie.
6–5 1
1/x 3 Omgekeerde. 1–18 1
10x{ ( Gewone anti-log.
Geeft 10 in de macht ×.
4–2 1
%{P Percent.
Geeft (y × x) ÷ 100.
4–6 1
%CHG z S Procentuele
verandering.
Geeft (x – y)(100 ÷ y).
4–6 1
πz M Geeft de benadering
3,14159265359 (12 cijfers).
4–3 1
Σ+6 Accumuleert (y, x) in statistische
registers.
12–2
Σ–z 4 Verwijdert (y, x) uit
statistische registers.
12–2
Naam Toetsen en omschrijving Pagina

Index van bewerkingen G-3
Σx{ 5Õ (;º)
Geeft de som van de x-waarden.
12–11 1
Σx2{ 5ÕÕÕ (;º)
Geeft de som van de kwadraten van
de x-waarden.
12–11 1
Σxy {5ÕÕÕÕÕ
(;º¸)
Geeft de som van de producten van
de x- en y-waarden.
12–11 1
Σy{ 5ÕÕ (;¸)
Geeft de som van de y-waarden.
12–11 1
Σy2{ 5ÕÕÕÕ (;¸)
Geeft de som van de kwadraten van
de y-waarden.
12–11 1
σx{ 2ÕÕ (σº)
Geeft standaarddeviatie van een
populatie van x-waarden:
12–7 1
σy{ 2ÕÕÕ (σ¸)
Geeft standaarddeviatie van een
populatie van y-waarden:
12–7 1
∫ FN d variabele z) ( ∫ G _) variabele
Integreert de weergegeven
vergelijking of het programma
geselecteerd door FN= met gebruik
van de lagere grens van de variabele
van integratie in het Y-register en de
bovengrens van de variabele van
intergratie in het X-register.
8–2
15–7
( ) 4haakjes. Druk op Õ om de
haakjes te laten voor meer
berekeningen.
6–6 1
Naam Toetsen en omschrijving Pagina
nxxi÷−
∑2
)(
nyyi÷−
∑2
)(

G-4 Index van bewerkingen
[ ] {3: een vector symbool voor het
uitvoeren van vector bewerkingen
10–1 1
θ
{?: een complex getal symbool
voor het uitvoeren van complexe getal
bewerkingen
9–1 1
A tot en met Z K variabele Waarde van
genoemde variabele.
6–4 1
ABS { A Absolute value.
Geeft .
4–17 1
ACOS { O Arc cosinus.
Geeft cos –1x.
4–4 1
ACOSH z 7{ O
Hyperbolische arc cosinus.
Geeft cosh –1 x.
4–6 1
9()Activeert algebraïsche berekeningen. 1–9
ALOG { ( Gewone anti-log.
Geeft 10 in de aangegeven macht
(antilogaritme).
6–16 1
ALL z8()
Toont alle significante cijfers. Moet
misschien naar rechts ({Õ)
schuiven om alle cijfers te kunnen zien.
1–23
AND z>(1AND)
Logische operator
11–4 1
ARG z=
Vervangt een complex getal met zijn
argument ”θ”
4–17 1
ASIN { LArc sinus
Geeft sin –1 x.
4–4 1
ASINH z 7{ L
Hyperbolische arc sinus.
Geeft sinh –1 x.
4–6 1
ATAN { R Arc tangens.
Geeft tan –1 x.
4–4 1
Naam Toetsen en omschrijving Pagina
x
Product specificaties
| Merk: | HP |
| Categorie: | Rekenmachine |
| Model: | 35s scientific calculator |
Heb je hulp nodig?
Als je hulp nodig hebt met HP 35s scientific calculator stel dan hieronder een vraag en andere gebruikers zullen je antwoorden
Handleiding Rekenmachine HP

1 Mei 2023

16 April 2023

12 Maart 2023

23 December 2022

28 Januari 2023

5 Januari 2023

15 Augustus 2022

17 Augustus 2022

17 Augustus 2022

16 Augustus 2022
Handleiding Rekenmachine
- Rekenmachine Braun
- Rekenmachine Casio
- Rekenmachine Canon
- Rekenmachine Addimult
- Rekenmachine Basetech
- Rekenmachine Genius
- Rekenmachine Global Tronics
- Rekenmachine GlobalTronics
- Rekenmachine Ibico
- Rekenmachine Lexibook
- Rekenmachine Rex
- Rekenmachine Sanyo
- Rekenmachine Sencor
- Rekenmachine Sharp
- Rekenmachine Sigma
- Rekenmachine Taurus
- Rekenmachine Texas
- Rekenmachine Texas Instruments
- Rekenmachine Tiger
- Rekenmachine United Office
- Rekenmachine Victor
- Rekenmachine Olivetti
- Rekenmachine Olympia
- Rekenmachine Omron
- Rekenmachine Citizen
- Rekenmachine Trevi
- Rekenmachine Genie
- Rekenmachine Aurora
- Rekenmachine Calculated Industries
- Rekenmachine Milan
- Rekenmachine Q-CONNECT
- Rekenmachine Rexel
- Rekenmachine XD Enjoy
- Rekenmachine Victor Technology
Nieuwste handleidingen voor Rekenmachine

30 Maart 2025

21 Maart 2025

21 Maart 2025

21 Maart 2025

21 Maart 2025

14 December 2024

1 December 2024

23 November 2024

23 November 2024

18 November 2024












